各种加法器的比对分析与Verilog实现（2）

      本文将介绍Kogge-Stone加法器和brent-kung加法器的原理，在下一篇博客中我将用Verilog进行实现。

目录

1. 并行前缀加法器(Parallel-Prefix Adder, PPA) 

2. Kogge-Stone加法器原理

3. brent-kung加法器原理

1. 并行前缀加法器(Parallel-Prefix Adder, PPA) 

       为了减少AND门的深度，PPA对CLA进行了进一步优化。不过PPA和CLA进行的计算流程大致一致，只是在计算进位Ci的时候进行了充分的并行优化。在PPA的设计中，主要有两种结构组件：processing component 和 buffer component，两种结构的构造和逻辑意义如下：

        目前的多种PPA变体，其主要设计思路是在加法器范围、电路深度、节点输出数量和整体布线四点上做出均衡。常见的变体有下面三种（这里的结构图是递推的意思）：

2. Kogge-Stone加法器原理

参考文献：

A Parallel Algorithm for the Efficient Solutionof a General Class of Recurrence Equations

       Kogge-Stone加法器是利用Peter M. Kogge和Harold S.Stone于1972年提出的一种并行算法生成的一种树形加法器。

       下面是我的一部分理解：

       使用CLA的计算流程：

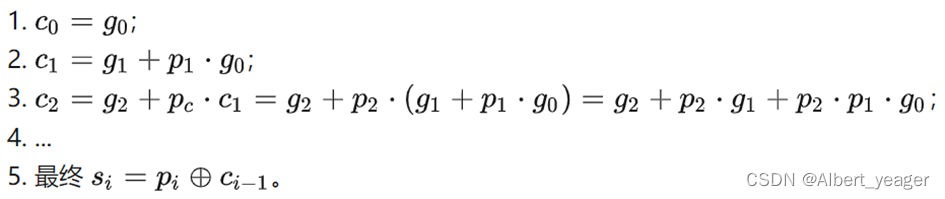
       可以把它抽象为下面的数学问题：

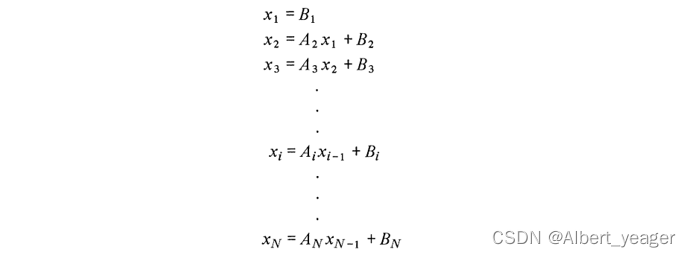
       为解决如上问题，论文中定义了下式：

       从而可以把问题转化为：

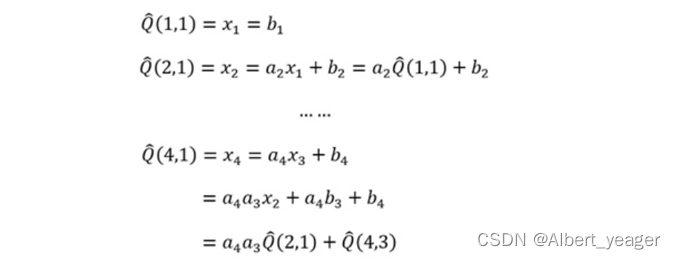
       因此递推公式如下：

        Q(i,1)和Q(2i,i+1)可以独立计算，Q(i,1)和Q(2i,i+1)又可以单独分解独立计算，每个层级都可以独立计算，因此加快了运算速度。

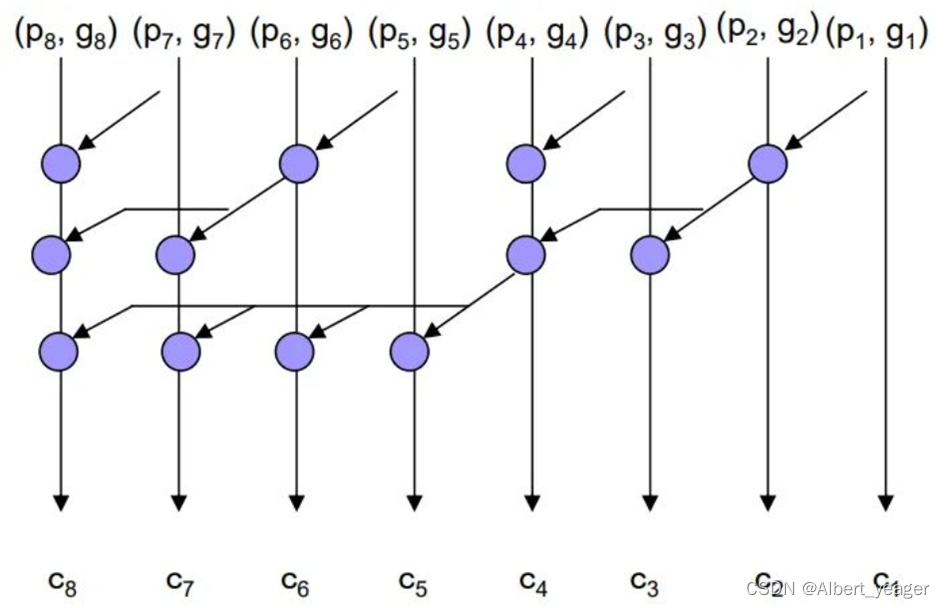
       然后就出现一张神奇的递推结构图（x8的计算图例）:

       以及X1至X8的计算步骤、系数与公式表：

       因此，可以比较快速的得出各项进位Ci：

       对于C1-C4等的生成，其算式如下：

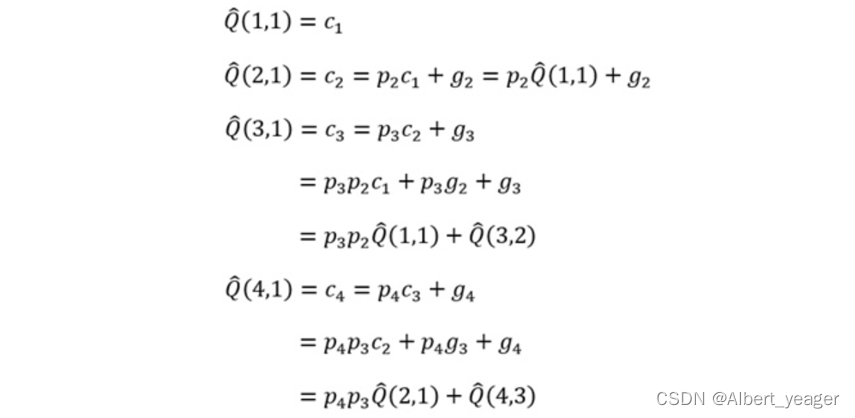
        这就是之前这张图的来源（就是把论文那张递推结构图倒过来）

3. brent-kung加法器原理

       brent-kung加法器是树形结构，由Richard P.Brent 和 H.T.Kung教授于上世纪80年代提出。设计的思想类似于超前进位加法器，但是brent和kung教授充分的考虑了开销和电路结构本身的拓扑学特性，针对性的升级了超前进位加法器的性能，使其达到了N比特加法器延迟正比于logN, 面积正比于N的效果。

       Brent-Kung加法器定义了以下运算“o”:

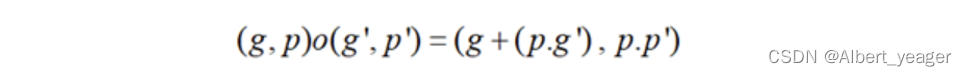
        也就是：

• 输入p,g,g’,p’，输出g+p.g’
• 输入p,g,g’,p’，输出p.p’

       可以用归纳出下面这个结论：

       当n=8时，（G8,P8）的计算方法如下图：

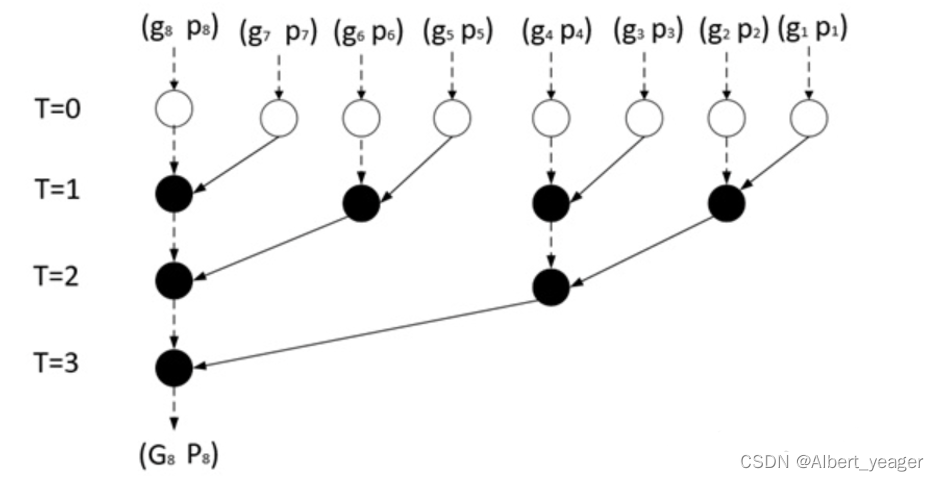
       其中白色圈表示数据传递，数据前后没有变化；黑色圈表示上文中定义的“o”操作，其计算示意图如下：

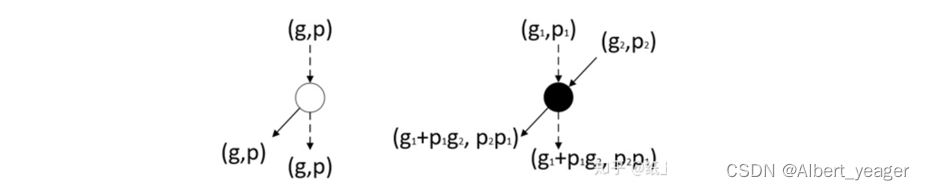
        在T=3时刻G8和P8的计算如下：

        （G8，P8）=（g8，p8）o（g7，p7）o（g6，p6）o（g5，p5）o（g4，p4）o（g3，p3）o（g2，p2）o（g1，p1）

       对于一般问题（Gi,Pi），i=1,2,3，…N的计算，其结构图如下：

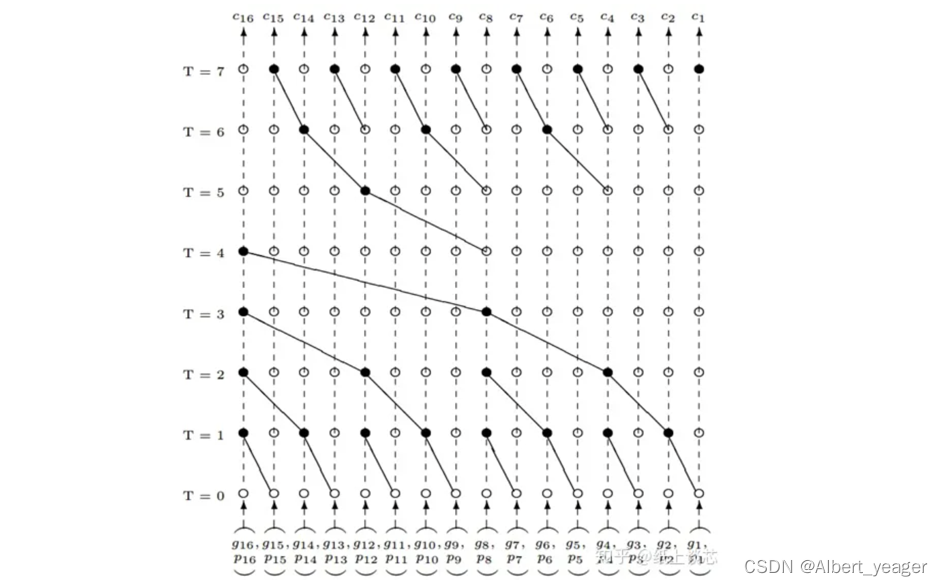
       brent-kung加法器主要展示了一种在电路上无法直接减少面积增加速度的情况下，进行数学上的抽象建模并优化结构的思路。二进制可以表示一切函数关系，这是二进制的完备性，因此我们可以把一切电路问题优化为数学问题进而求解，这种一种非常重要的思路。

       从逻辑层数，扇入扇出和布线拥塞度三个方面看该树形加法器，Brent-Kung加法器的拓扑结构经历逻辑层数较多，需要(2logN–1)级，扇入扇出和布线拥塞度较低。

体会：我认为，不论是Kogge-Stone方法还是brent-kung方法，本质上都是在CLA的基础上，对Ci=Gi+Pi·Ci-1这个递推式进行转化，用类似于整体代换的思想，解决CLA中随着i增大，Ci通项表达式复杂度疯狂上升的问题。有点类似于编程里从算法上降低时间复杂度的感觉。但是这必然会造成空间复杂度的上升，在硬件上的体现可能就是布线更加拥堵。

参考链接：

Kogge-Stone加法器原理与设计

Brent-Kung树形加法器原理与设计

求学路上，你我共勉(๑•̀ㅂ•́)و✧