本文主要是介绍KMeans算法在RFM模型(用户分层模型)上的应用,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
KMeans在RFM模型上的应用
RFM模型到底是个啥,建议先参考百度百科以及知乎的解释。
KMeans算法又是个啥,一言以蔽之:无监督学习的聚类算法(也就是俗话讲的物以类聚,人以群分)。
废话不多说,开始上手
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
data = pd.read_excel('./consumption_data.xls', index_col='Id')
data.head()
解释下这个数据集:字段R表示最近一次消费(Recency),字段F表示消费频率(Frequency),字段M表示消费金额(Monetary)
- 字段R:最近一次消费指上一次购买的时间——用户上一次是什么时候下的单、用户上一次是什么时候订购的服务,或在线下门店中用户上一次进店购买是什么时候。
- 字段F:消费频率指的是顾客在限定的期间内所购买的次数。一般而言,最常购买的用户,也是满意度/忠诚度最高的顾客,同时也是对品牌认可度最高的用户。
- 字段M:消费金额是电商相关业务数据库的支柱,也可以用来验证“帕雷托法则”——公司80%的收入来自20%的顾客。M值带有时间范围,指的是一段时间(通常是1年)内的消费金额。对于一般电商店铺而言,M值对客户细分的作用相对较弱(因为客单价波动幅度不大)。
| R | F | M | |
|---|---|---|---|
| Id | |||
| 1 | 27 | 6 | 232.61 |
| 2 | 3 | 5 | 1507.11 |
| 3 | 4 | 16 | 817.62 |
| 4 | 3 | 11 | 232.81 |
| 5 | 14 | 7 | 1913.05 |
data.shape
(940, 3)
data.index
Int64Index([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,...933, 934, 935, 936, 937, 938, 939, 940, 941, 942],dtype='int64', name='Id', length=940)
数据标准化
data_std = 1.0 * (data - data.mean()) / data.std()
data_std.head()
| R | F | M | |
|---|---|---|---|
| Id | |||
| 1 | 0.764186 | -0.493579 | -1.158711 |
| 2 | -1.024757 | -0.630079 | 0.622527 |
| 3 | -0.950217 | 0.871423 | -0.341103 |
| 4 | -1.024757 | 0.188922 | -1.158432 |
| 5 | -0.204824 | -0.357079 | 1.189868 |
k =8 # k-1个簇
iteration = 500 # 聚类最大循环次数
inertia = [] # 簇内误差平方和
for i in range(1, k):model = KMeans(n_clusters=i, n_jobs=4, max_iter=iteration, random_state=1234)model.fit(data_std)inertia.append(model.inertia_)
font = {'family':'SimHei', 'size':'20'}
plt.rc('font', **font)
plt.figure(figsize=(20,6))
plt.plot(range(1, k), inertia)
plt.title('查看最佳k值', fontsize=20)
plt.xlabel('簇的数量')
plt.ylabel('簇内误差平方和')
plt.show()
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RP58bDaK-1645165442623)(output_8_0.png)]
label = pd.Series(model.labels_)
labels = label.value_counts()
labels # 每个类簇的样本数
1 218
2 189
5 182
6 173
0 144
4 28
3 6
dtype: int64
centers = pd.DataFrame(model.cluster_centers_)
centers # 簇类中心
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 0.488287 | 1.153902 | 0.260323 |
| 1 | -0.206534 | -0.546175 | 0.766205 |
| 2 | 0.496397 | -0.645968 | -0.674198 |
| 3 | 0.863572 | 0.712173 | 7.363321 |
| 4 | 4.025280 | -0.137703 | 0.273264 |
| 5 | -0.643460 | -0.727579 | -0.853512 |
| 6 | -0.692992 | 1.196498 | 0.152670 |
# 拼接类簇的数目和簇类中心
output = pd.concat([labels, centers], axis=1)
output
| 0 | 0 | 1 | 2 | |
|---|---|---|---|---|
| 0 | 144 | 0.488287 | 1.153902 | 0.260323 |
| 1 | 218 | -0.206534 | -0.546175 | 0.766205 |
| 2 | 189 | 0.496397 | -0.645968 | -0.674198 |
| 3 | 6 | 0.863572 | 0.712173 | 7.363321 |
| 4 | 28 | 4.025280 | -0.137703 | 0.273264 |
| 5 | 182 | -0.643460 | -0.727579 | -0.853512 |
| 6 | 173 | -0.692992 | 1.196498 | 0.152670 |
KMeans追求的效果是:同一聚类内部距离最小化,不同聚类组间距离最大化
其实,聚类处理到这一步,已经可以有一些结论出来了。上面我们聚了7个类别,实际有的类别所包含的样本量比较少,例如类别3和类别4,所以可以重新把上面的步骤跑一遍,然后把k值设置更小一些。
output.columns = ['样本数', 'R', 'F', 'M']
output.columns
Index(['样本数', 'R', 'F', 'M'], dtype='object')
output
| 样本数 | R | F | M | |
|---|---|---|---|---|
| 0 | 144 | 0.488287 | 1.153902 | 0.260323 |
| 1 | 218 | -0.206534 | -0.546175 | 0.766205 |
| 2 | 189 | 0.496397 | -0.645968 | -0.674198 |
| 3 | 6 | 0.863572 | 0.712173 | 7.363321 |
| 4 | 28 | 4.025280 | -0.137703 | 0.273264 |
| 5 | 182 | -0.643460 | -0.727579 | -0.853512 |
| 6 | 173 | -0.692992 | 1.196498 | 0.152670 |
output.iloc[3]['F']
0.71217272223757799
详细标记原始数据每个样本的类别
model.labels_
array([2, 1, 6, 5, 1, 2, 5, 2, 2, 6, 5, 2, 1, 0, 1, 6, 4, 2, 5, 2, 5, 1, 6,2, 2, 0, 1, 1, 2, 3, 6, 2, 5, 1, 6, 6, 5, 1, 1, 2, 5, 6, 5, 5, 6, 1,2, 2, 6, 6, 1, 1, 1, 6, 2, 2, 1, 4, 1, 2, 5, 0, 6, 1, 1, 2, 1, 1, 2,1, 0, 0, 5, 2, 1, 5, 4, 6, 6, 1, 2, 2, 5, 2, 5, 6, 0, 2, 5, 0, 4, 5,6, 6, 2, 1, 6, 2, 6, 6, 5, 2, 4, 0, 0, 5, 5, 0, 0, 5, 2, 6, 1, 5, 2,2, 5, 2, 4, 0, 2, 1, 5, 2, 2, 2, 5, 2, 2, 0, 1, 2, 5, 5, 2, 2, 5, 2,4, 2, 1, 1, 5, 0, 2, 5, 5, 2, 0, 1, 6, 1, 6, 5, 2, 2, 1, 5, 1, 1, 1,0, 2, 2, 5, 5, 5, 5, 0, 5, 0, 6, 6, 1, 2, 1, 2, 2, 6, 5, 0, 5, 1, 2,2, 6, 2, 6, 6, 1, 2, 0, 4, 2, 1, 1, 1, 1, 5, 5, 5, 5, 2, 5, 5, 1, 2,2, 1, 1, 5, 5, 0, 6, 2, 5, 5, 2, 0, 2, 1, 6, 1, 5, 2, 3, 5, 1, 5, 6,2, 2, 1, 1, 1, 2, 2, 1, 5, 5, 5, 1, 1, 0, 5, 1, 5, 2, 5, 6, 6, 0, 1,5, 4, 2, 2, 2, 1, 0, 5, 6, 1, 1, 6, 2, 6, 2, 4, 1, 2, 2, 1, 6, 0, 6,1, 6, 5, 1, 1, 4, 2, 1, 2, 1, 0, 0, 1, 5, 6, 2, 5, 5, 1, 1, 5, 4, 5,4, 0, 6, 5, 0, 1, 1, 5, 1, 6, 2, 5, 6, 2, 1, 5, 1, 6, 4, 1, 0, 2, 5,1, 6, 6, 1, 2, 5, 1, 6, 5, 0, 4, 1, 0, 0, 2, 6, 3, 6, 5, 2, 1, 2, 0,5, 5, 1, 5, 0, 2, 5, 2, 6, 5, 0, 2, 6, 0, 5, 1, 6, 0, 2, 6, 2, 2, 0,1, 2, 2, 0, 6, 6, 1, 2, 6, 5, 2, 6, 2, 6, 5, 1, 5, 1, 1, 6, 5, 5, 6,5, 6, 0, 2, 0, 5, 1, 6, 2, 1, 6, 6, 2, 6, 0, 0, 0, 1, 6, 2, 6, 6, 1,6, 6, 6, 5, 4, 1, 5, 6, 5, 0, 0, 2, 1, 6, 0, 0, 1, 5, 1, 6, 0, 1, 0,1, 0, 2, 6, 6, 5, 6, 5, 0, 5, 2, 6, 5, 1, 2, 1, 6, 5, 1, 5, 6, 6, 5,6, 5, 0, 5, 0, 0, 6, 1, 0, 6, 0, 0, 5, 2, 0, 1, 0, 2, 1, 6, 1, 1, 6,3, 5, 2, 1, 1, 5, 5, 2, 6, 6, 1, 6, 5, 1, 0, 1, 0, 6, 1, 1, 1, 5, 1,1, 0, 5, 6, 0, 1, 0, 0, 1, 0, 5, 0, 5, 2, 1, 2, 6, 0, 3, 1, 2, 1, 2,5, 0, 2, 6, 0, 5, 1, 2, 0, 0, 6, 6, 1, 0, 5, 0, 1, 1, 6, 5, 1, 2, 5,0, 1, 1, 0, 2, 6, 1, 1, 0, 1, 5, 1, 1, 5, 5, 0, 0, 1, 1, 6, 6, 1, 0,2, 0, 6, 1, 6, 2, 1, 2, 5, 5, 6, 2, 2, 6, 0, 5, 2, 2, 6, 0, 5, 0, 6,5, 0, 0, 5, 5, 2, 1, 6, 0, 2, 0, 1, 5, 4, 2, 2, 5, 5, 2, 5, 1, 0, 1,2, 0, 6, 5, 4, 1, 1, 2, 0, 6, 6, 1, 5, 0, 6, 0, 1, 1, 5, 4, 1, 6, 0,2, 2, 1, 5, 1, 0, 2, 6, 2, 4, 0, 6, 5, 5, 0, 2, 1, 1, 5, 1, 6, 0, 1,6, 1, 4, 6, 6, 6, 1, 1, 1, 1, 0, 1, 5, 1, 5, 0, 2, 6, 5, 5, 2, 5, 1,0, 1, 1, 0, 1, 6, 1, 1, 1, 1, 4, 6, 1, 2, 1, 1, 2, 6, 2, 2, 6, 1, 2,5, 6, 6, 5, 5, 1, 1, 4, 0, 6, 5, 5, 5, 5, 1, 0, 1, 6, 5, 1, 0, 0, 5,2, 4, 2, 2, 2, 1, 6, 2, 5, 5, 5, 2, 1, 2, 5, 5, 0, 0, 6, 6, 2, 6, 1,0, 0, 6, 0, 2, 0, 0, 2, 6, 6, 0, 0, 1, 2, 6, 6, 5, 5, 6, 5, 6, 6, 2,1, 1, 5, 5, 1, 1, 2, 6, 2, 4, 2, 4, 6, 5, 0, 2, 6, 0, 6, 6, 5, 6, 1,0, 0, 5, 6, 1, 5, 5, 5, 5, 2, 2, 1, 6, 0, 6, 5, 6, 0, 2, 1, 0, 2, 1,2, 0, 1, 6, 2, 2, 0, 2, 5, 0, 1, 0, 0, 6, 5, 1, 1, 5, 2, 6, 1, 5, 2,5, 2, 2, 2, 1, 1, 0, 1, 1, 0, 6, 5, 5, 6, 5, 1, 0, 6, 2, 1, 0, 0, 2,0, 0, 6, 6, 1, 2, 1, 4, 0, 1, 6, 5, 1, 6, 2, 2, 0, 6, 6, 2, 1, 6, 1,6, 2, 4, 2, 2, 1, 2, 2, 0, 1, 6, 5, 2, 6, 6, 5, 1, 6, 1, 2, 5, 5, 2,6, 1, 2, 2, 0, 1, 6, 0, 0, 0, 1, 6, 3, 6, 1, 1, 5, 1, 2, 2])
data.index
Int64Index([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,...933, 934, 935, 936, 937, 938, 939, 940, 941, 942],dtype='int64', name='Id', length=940)
summary = pd.concat([data, pd.Series(model.labels_, index=data.index)], axis=1)
summary.head()
| R | F | M | 0 | |
|---|---|---|---|---|
| Id | ||||
| 1 | 27 | 6 | 232.61 | 2 |
| 2 | 3 | 5 | 1507.11 | 1 |
| 3 | 4 | 16 | 817.62 | 6 |
| 4 | 3 | 11 | 232.81 | 5 |
| 5 | 14 | 7 | 1913.05 | 1 |
summary.columns = ['R', 'F', 'M', 'label']
summary.head()
| R | F | M | label | |
|---|---|---|---|---|
| Id | ||||
| 1 | 27 | 6 | 232.61 | 2 |
| 2 | 3 | 5 | 1507.11 | 1 |
| 3 | 4 | 16 | 817.62 | 6 |
| 4 | 3 | 11 | 232.81 | 5 |
| 5 | 14 | 7 | 1913.05 | 1 |
summary.info()
<class 'pandas.core.frame.DataFrame'>
Int64Index: 940 entries, 1 to 942
Data columns (total 4 columns):
R 940 non-null int64
F 940 non-null int64
M 940 non-null float64
label 940 non-null int32
dtypes: float64(1), int32(1), int64(2)
memory usage: 33.0 KB
# 类别0
dd = summary[summary['label'] == 0]
dd.info()
<class 'pandas.core.frame.DataFrame'>
Int64Index: 144 entries, 13 to 929
Data columns (total 5 columns):
Id 144 non-null int64
R 144 non-null int64
F 144 non-null int64
M 144 non-null float64
label 144 non-null int64
dtypes: float64(1), int64(4)
memory usage: 6.8 KB
# 用户群0(label=0)
plt.figure(figsize=(12,9))
plt.subplot(311)
dd['R'].plot(kind='kde')
plt.legend()
plt.subplot(312)
dd['F'].plot(kind='kde')
plt.legend()
plt.subplot(313)
dd['M'].plot(kind='kde')
plt.legend()
plt.show()
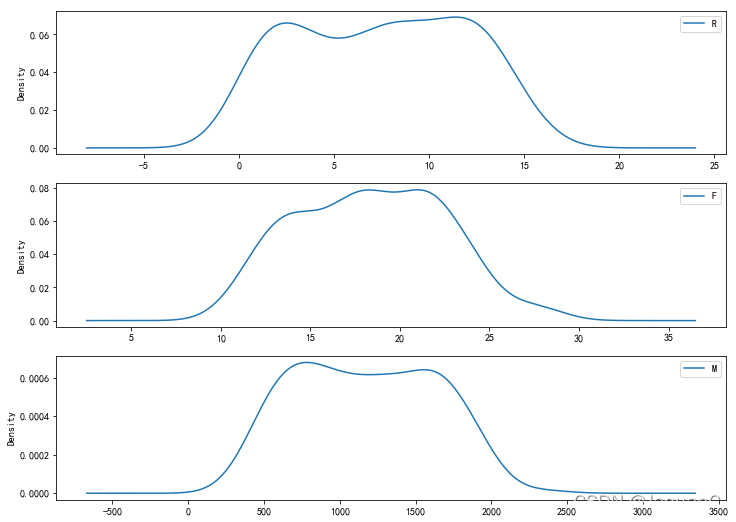
分群0的特点
- R 间隔多分布在0到15天左右
- F 消费频率集中在10到25次
- M 消费金额集中在500到2000左右
# 用户群1(label=1)
dd1 = summary[summary['label'] == 1]plt.figure(figsize=(12,9))
plt.subplot(311)
dd1['R'].plot(kind='kde')
plt.legend()
plt.subplot(312)
dd1['F'].plot(kind='kde')
plt.legend()
plt.subplot(313)
dd1['M'].plot(kind='kde')
plt.legend()
plt.show()
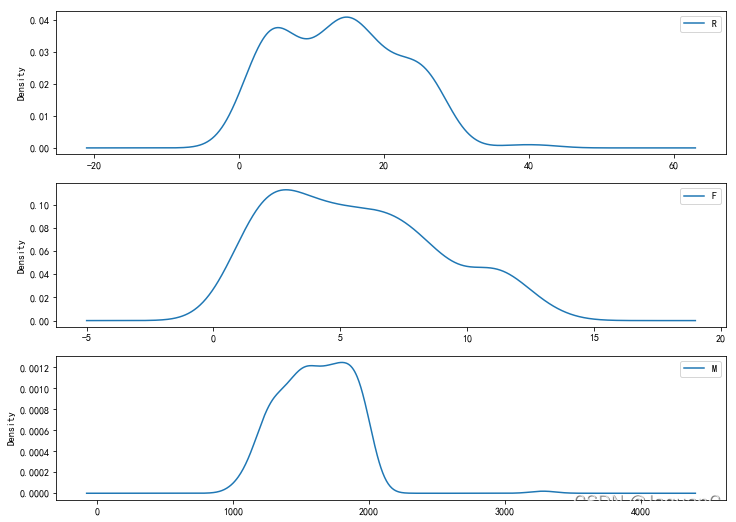
分群1的特点
- R 间隔多分布在0到35天左右
- F 消费频率集中在0到12次
- M 消费金额集中在1000到2000左右
其他用户的分群同理,都可以整理出来。
那么问题来了,整理这些分群特点有什么用处呢?
用处就是可以把用户拆分成不同的用户包,支持后期对用户的精细化运营,例如给不同的用户群设置不同额度的优惠券,或者给不同的用户群推广不同价位的商品等等。
-------------------------------------END--------------------------------------------
这篇关于KMeans算法在RFM模型(用户分层模型)上的应用的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



