点云迭代最近邻点配准法_一种利用三维点云的零件加工精度自动检测方法与流程...

本发明属于机械加工检测技术，具体涉及一种利用三维点云的零件加工精度自动检测方法。

背景技术：

三维激光扫描是一种近年来快速发展的三维空间成像技术，利用双轴伺服电机驱动激光测距器，对扫描场景的目标表面进行等间隔的连续采样，输出与三维场景几何形态完全一致的三维点云。这种技术正在被越来越广泛地应用于测绘、考古、机械加工制造、三维打印、机器人、无人驾驶等领域。

机械零件是制造业的基础，加工精度检测是保证精密零件产品质量的关键生产环节，也是长期制约我国高精尖产业发展的技术瓶颈。传统的机械零件质检方法主要使用卡尺、微分尺、三维坐标仪等接触式测量方法，依赖人工频繁选点，测量结果容易受到选点误差的影响。三维扫描技术作为一种可以快速获取高精度、高密度物体表面采样点的非接触测量技术可以有效解决这些问题。

近年来，研究人员开始尝试利用三维扫描技术进行零件精度检测，提出了各自的全表面非接触检测方案。然而这些方法在配准实物扫描点云和设计模型时，均未考虑零件表面加工误差部位会造成配准结果整体偏差问题。此外，公开报道的检测方案都是在配准基础上直接进行零件表面偏差计算，将结果简单地标记在点云上显示出来，需要质检人员依靠人眼区分点云测量随机误差与零件表面的加工误差。

技术实现要素：

发明目的：本发明的目的在于解决现有技术中存在的不足，提供一种利用三维点云的零件加工精度自动检测方法，通过三维激光扫描技术采集零件点云，与设计模型精细化配准，再利用误差分布假设性检验和公差界限检验实现机械零件精度的自动化检测。

技术方案：本发明的一种利用三维点云的零件加工精度自动检测方法，通过以下具体步骤对一对给定零件以及零件设计模型进行自动检测

(1)针对零件实体，利用三维激光扫描技术对零件进行点云采样，采集零件三维点云P；

(2)通过主成分分析法对采样点云P与零件设计模型Q进行粗配准，根据采样点云P配准过程中点的残差值对点对D0赋权，通过选权迭代最近邻点的方法进行配准精细调整；

(3)配准完成后进行误差分布假设性检验以及公差界限检验自动生成零件加工精度的评价结果。

进一步的，所述步骤(2)的详细过程为：

(2.1)对于零件设计模型Q进行随机采样，获得点集Q0；

(2.2)对点云P和点集Q0分别通过主成分分析法计算各自的协方差矩阵，然后将对应协方差矩阵的特征向量作为XYZ轴建立各自标准姿态坐标系Cp和Cq；

(2.3)通过坐标转换把Cp和Cq转换到相同坐标系中完成粗配准；

(2.4)对完成粗配准的点云P，把零件设计模型Q作为参考，计算点云P到零件设计模型Q的最近距离点集Q1＝C(P，Q)，点云P与点集Q1具有一一对应关系，形成初始对应点对应关系D0；

(2.5)利用粗配准结果采样点云P中点的残差值和相应赋权函数对点对D0进行赋权：

其中，v为残差，μ为v的均值，σ为v的方差，n为常数；

(2.6)结合步骤(2.5)所得点对权值，计算旋转矩阵R和平移向量qT，对扫描点云P进行坐标变换；

(2.7)重复步骤(2.1)至步骤(2.3)过程，进行迭代计算，每次计算均更新点对应关系获得点对Dk，计算第k次迭代的配准误差为

其中，di(k)为第k次迭代P到X的距离，n为点云P点的数目，当|Ek-Ek-1|＜ε时，认为迭代收敛，此时结束精确配准。

进一步的，所述步骤(3)的详细过程为：

(3.1)采用χ2检验法进行误差分布假设性检验，检测加工偏差工件，如果本次检测通过，即：认为本次检测的距离偏差di服从正态分布；否则，认为距离偏差分布不服从正态分布，产品可能存在系统性的加工误差，将其认定为不合格产品；

(3.2)根据公差界限检验，在通过误差分布假设性检验的零件中检测加工粗糙零件；通过检测3倍中误差的绝对值是否小于公差界限Δ限来判断零件表面的粗糙程度，如果|3σ|＜Δ限则认为零件表面加工精细，满足加工精度要求，属于合格件；其中v是残差，n是采样点云点个数。

此处，本发明先使用χ2检验法进行误差分布假设性检验，χ2检验法具有极高的误差敏感度，能够对零件加工误差实现敏感识别；再公差界限检验检测零件加工粗糙度

进一步的，所述步骤(2.2)的具体内容为：

其中N为特征向量个数，为点云P的重心，以该重心为原点，以COV的特征向量为XYZ轴建立各自标准姿态直角坐标系Cp，Cq。

进一步的，所述步骤(2.3)的具体内容为：

根据Cp和Cq的坐标原点，平移坐标系Cp，使它的坐标原点与Cq的原点重合；

Cp方向向量为i、j、k，Cq三个坐标轴在Cp中的方向向量

其中a1，a2，a3分别为Cq中ox′与Cp中ox oy oz的夹角，b1，b2，b3分别为Cq中oy′与Cp中ox oy oz的夹角，c1，c2，c3分别为Cq中oz′与Cp中ox oy oz的夹角，那么就有

转换后Cp，Cq移动到相同坐标系中完成粗配准。

有益效果：本发明利用三维点云的零件加工精度自动检测方法，可以实现零件精度自动化检测，本发明所利用的选权迭代最进邻点的配准方法可以有效克服传统配准方法易受零件加工偏差影响的弊端，可以有效排除点云噪声点对配准的干扰，具有较强的鲁棒性。在精度评定方面，该方法对加工偏差以及表面加工粗糙的零件具有很强的敏感性，并且可以满足不同零件或者工厂的不同精度要求，在工业生产中具有广泛的适应性。

另外，本发明考虑现有技术中加工误差区域对配准精度存在影响的问题，以及配准过程始终使用固定不变的参考点集的问题，本发明采用迭代计算的配准方法，并且在迭代过程中不断更新参考点集，通过不断调整权值让有可能存在加工误差的区域退出配准计算，从而最大限度的提高配准精度。

附图说明

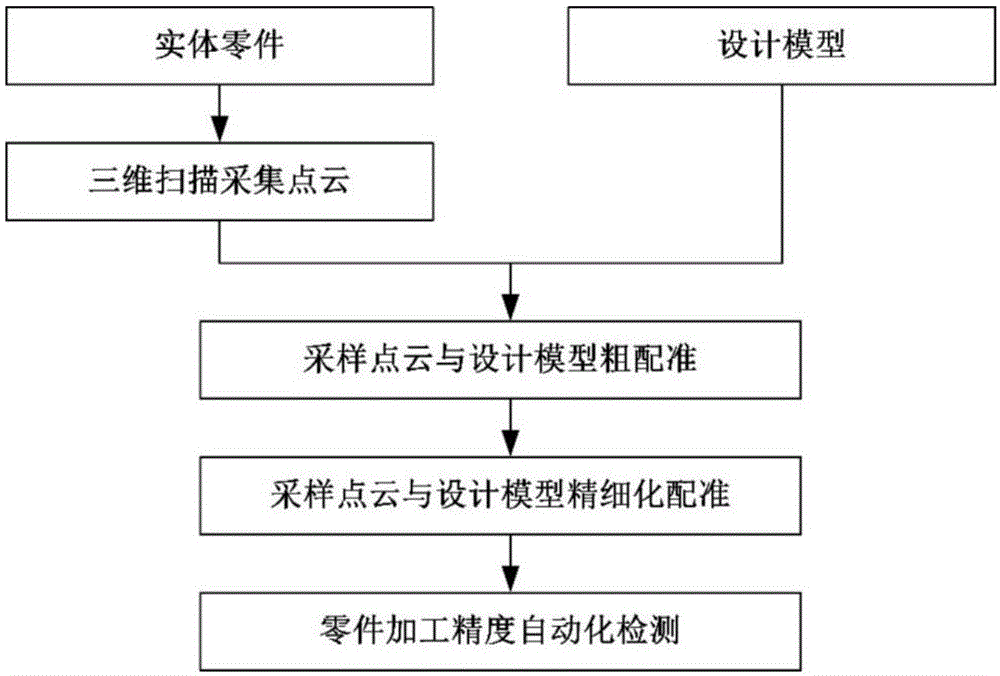
图1为本发明的整体流程图。

图2为本发明中标准姿态直角坐标系示意图。

图3为本发明中采样点云与设计模型粗配准示意图。

图4为本发明中采样点云与设计模型点对选择示意图。

图5为本发明中采样点云误差分布假设性检验示意图。

图6为实施例中采样点云公差界限检验示意图。

具体实施方式

下面对本发明技术方案进行详细说明，但是本发明的保护范围不局限于所述实施例。

如图1所示，本发明的利用三维点云的零件加工精度自动检测方法，给定一对零件以及零件设计模型，该检测方法包含以下步骤：

(1)针对零件实体，利用三维激光扫描技术对零件进行点云采样，采集零件三维点云P；

(2)通过主成分分析法对采样点云与零件设计模型进行粗配准，根据采样点云配准过程中点的残差值对点赋权，通过选权迭代最近邻点的方法进行配准精细调整，具体内容为：

(2.1)对于零件设计模型Q进行随机采样，获得点集Q0；

(2.2)对点云P，Q0分别通过主成分分析法计算各自的协方差矩阵COV

其中N为特征向量个数，为点云的重心，以重心为原点，以COV的特征向量为XYZ轴建立各自标准姿态直角坐标系Cp，Cq，如图2所示；

(2.3)根据Cp，Cq的坐标原点，平移坐标系Cp，使它的坐标原点与Cq的原点重合；

Cp方向向量为i、j、k，Cq三个坐标轴在Cp中的方向向量

其中a1，a2，a3分别为Cq中ox′与Cp中ox oy oz的夹角，b1，b2，b3分别为Cq中oy′与Cp中ox oy oz的夹角，c1，c2，c3分别为Cq中oz′与Cp中ox oy oz的夹角，那么就有，

转换后Cp，Cq移动到相同坐标系中完成粗配准，如图3所示；

(2.4)对完成粗配准的点云P，把设计模型Q作为参考，查找最近点，计算点云P到设计模型Q的最近距离点集Q1＝C(P，Q)，如图4示所示，点集P与Q1具有一一对应关系，形成初始对应点对应关系D0；

(2.5)利用粗配准结果采样点云P中点的残差值和本发明设计赋权函数对点对D0进行赋权

其中，v为残差，μ为v的均值，σ为v的方差，n可以取5，μ可以取0；

(2.6)结合点对权值，计算扫描点云P的重心μp和对应点点集X的重心μx

根据重心计算P和Q1的加权协方差矩阵CPX

求CPX的反对称矩阵A，A中各元素

通过Aij构造列矢量Δ＝[A23，A31，A12]T，根据列矢量Δ和CPX构造如下式所示的四阶对称矩阵：

其中I3为三阶单位矩阵。接下来，求出对应矩阵Q的最大特征值的单位特征矢量qR。

矢量qR即为所求最优旋转矩阵对应的单位四元数表达，构建旋转矩阵：

再根据

qT＝μx-R(qR)μp

计算对应的平移向量qT。依据旋转矩阵R和平移向量qT，对扫描点集P进行坐标变换；

(2.7)重复步骤(2.1)到步骤(2.3)过程，进行迭代计算，每次计算更新点对应关系获得点对Dk，计算第k次迭代的配准误差为

其中，di(k)为第k次迭代P到X的距离。当|Ek-Ek-1|＜ε时，认为迭代收敛，此时结束精确配准，ε可以取10-5。

上述步骤中利用全部点云进行配准，①不用去额外提取“特征点集”，减少了计算步骤，提高了采集点云的利用率，②在ICP迭代过程中，通过选权的方法逐步消除误差点对配准的影响(2.5)，消除普通ICP方法的弊端，在配准过程中将误差点和非误差点隔离开来，互不影响。

(3)配准完成后进行误差分布假设性检验以及公差界限检验自动生成零件加工精度的评价结果，详细过程为：

(3.1)采样χ2检验法进行误差分布假设性检验，检测加工偏差工件。

设距离偏差值di为质量特性值xi，其分布函数为F(x)，正态分布函数为F0(x)，根据xi来检验下述原假设是否成立

H0：F(x)＝F0(x)

根据xi估计F0(x)的两个参数μ和σ，以确定正态分布函数F0(x)的具体形式。这样就可以在假设H0下，计算出xi落入k组中的概率pi，以及由pi与点数量n(即样本容量)的乘积算出理论频数np1，np2，...，nPk，此处k为22。因此，采用检验统计量χ2来描述它们之间的偏离程度，根据χ2的大小判断它们之间的差异是由样本的随机性引起的，还是由于F(x)≠F0(x)所引起的。

进行检验时，根据事先给定的显著水平α，例如：α取0.05，利用

查找χ2分布表可得临界值

最后将计算得出的χ2与相比较：如果则接受H0，即：认为本次检测的距离偏差di服从正态分布；否则，认为距离偏差分布不服从正态分布，产品可能存在系统性的加工误差，将其认定为不合格产品。如图5所示，此零件(图5左)通过误差分布假设性检验，而带有系统误差的零件(图5右)不能通过，判为不合格产品。

(3.2)根据公差界限检验，在通过误差分布假设性检验的零件中检测加工粗糙零件。

计算采样点云中误差

其中v是残差，n是采样点云点个数。

通过检测3倍中误差的绝对值是否小于公差界限Δ限，Δ限根据零件精度标准制定，来判断零件表面的粗糙程度，例如：Δ限＝0.07。如果|3σ|＜Δ限则认为零件表面加工精细，满足加工精度要求，属于合格件。如图6所示，此零件|3σ|＞Δ限，未能通过公差界限检验，判为次品零件。

通过上述实施例可看出，精细化配准是实现零件精度自动化检测的重要前提，而本发明利用选权迭代的最近邻点的配准方法，实现高精度配准，能真实反映零件与设计模型的差别，在配准结束后，通过误差分布假设性检验有效检测出加工出现偏差的不合格零件，最后通过公差界限检验，找出零件表面加工粗糙的次品零件，最终实现快速精确的自动化零件精度检测。