本文主要是介绍[Ural1519] Formula 1,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Description
给出 n∗m n ∗ m 的方格,有些格子不能走,其它格子必须走,形成一个闭合回路。问有多少种走法?
( n≤12 n ≤ 12 m≤12 m ≤ 12 )
Solution
插头DP辣!!!(练习板子题
一年前就听说这个东西,然后觉得太强了不敢学 qwq q w q ,我好菜菜啊。
终于在这篇好博客的指引下:戳我戳我:),学习到了什么是插头DP。
可以看上面那个大佬的博客入门很好哒!本白菜以为那位大佬讲的和写的不太一样啊,就自己按照讲的做法写了一个,可以对!
主要思想就是括号表示法和插头的转移。似乎还有一个做法是“最小表示法”,但是括号的相比起来又快又方便写。插头转移的话就去看一下连到自己的插头的情况分类讨论即可。
还有一个小地方就是我们本来是三进制的,为了快,改成了四进制。然后状态就要用 hash h a s h 表存了。
复杂度大约是 O(3mnm2) O ( 3 m n m 2 ) ??但是绝对满不了,有很多无用状态。
Other
扩展一下求哈密顿路径怎么办? cdq c d q 说我们再加一个插头状态,就是“独立插头”?(原来是“没有插头”“左括号插头”“右括号插头”),似乎有一点道理??
独立插头大概意思应该是有那么一个插头它的另一端挂在上面不会下来了,所以它没有另一端,既不是左括号也不是右括号。假设你现在顺次有一个右括号和一个独立插头,你使右括号和独立插头连在一起,你要去找那个前面与这个右括号匹配的左括号,把它改成独立插头。当然还有别的几种情况要考虑。(一顿瞎BB还觉得自己很有道理
留坑,什么时候回来写一下试试。
(图扔上来就跑 qwq q w q
Source
//2018-4-26
//miaowey
//
//Ural1519
//Count the number of Hamilton circuit
//
#include <bits/stdc++.h>
using namespace std;#define LL long long
#define For(i, a, b) for(int i = (a); i <= (int)(b); ++i)
#define Forr(i, a, b) for(int i = (a); i >= (int)(b); --i)#define N 15
#define M 300000
const int P = 1e6 + 3;char rs[N];LL ans, f[2][M];
int n, m, ex, ey, o, tot[2], mp[N][N], zt[2][M], bit[N];int en, head[P], nxt[M], to[M];void Insert(int now, LL nval){int t = now % P;for(int i = head[t]; i; i = nxt[i])if(zt[o][to[i]] == now){f[o][to[i]] += nval; return;}++tot[o];to[++en] = tot[o]; nxt[en] = head[t]; head[t] = en;zt[o][tot[o]] = now; f[o][tot[o]] = nval;
}void PlugDp(){For(i, 1, 12) bit[i] = i << 1;o = 0; tot[o] = 1; f[o][1] = 1; zt[o][1] = 0;For(i, 1, n){For(j, 1, tot[o]) zt[o][j] <<= 2;For(j, 1, m){en = 0; memset(head, 0, sizeof head);tot[o ^= 1] = 0;For(k, 1, tot[o ^ 1]){int now = zt[o ^ 1][k]; LL nval = f[o ^ 1][k];int dw = (now >> bit[j]) & 3, ri = (now >> bit[j - 1]) & 3;if(!mp[i][j]){if(!dw && !ri) Insert(now, nval);}else if(!dw && !ri){if(mp[i][j + 1] && mp[i + 1][j]) Insert(now + (1 << bit[j - 1]) + 2 * (1 << bit[j]), nval);}else if(!dw && ri){if(mp[i][j + 1]) Insert(now - ri * (1 << bit[j - 1]) + ri * (1 << bit[j]), nval);if(mp[i + 1][j]) Insert(now, nval);}else if(dw && !ri){if(mp[i + 1][j]){Insert(now - dw * (1 << bit[j]) + dw * (1 << bit[j - 1]), nval);}if(mp[i][j + 1]) Insert(now, nval);}else if(dw == 1 && ri == 1){int cnt = 0;For(u, j + 1, m){int t = (now >> bit[u]) & 3;if(t == 1) ++cnt; else if(t == 2) --cnt;if(cnt == -1){Insert(now - (1 << bit[u]) - (1 << bit[j - 1]) - (1 << bit[j]), nval);break;}}}else if(dw == 2 && ri == 2){int cnt = 0;Forr(u, j - 2, 0){int t = (now >> bit[u]) & 3;if(t == 1) ++cnt; else if(t == 2) --cnt;if(cnt == 1){Insert(now + (1 << bit[u]) - 2 * (1 << bit[j - 1]) - 2 * (1 << bit[j]), nval);break;}}}else if(dw == 1 && ri == 2) Insert(now - ri * (1 << bit[j - 1]) - dw * (1 << bit[j]), nval);else if(dw == 2 && ri == 1 && i == ex && j == ey) ans += nval;}}}
}int main(){
#ifndef ONLINE_JUDGEfreopen("test.in", "r", stdin);freopen("test.out", "w", stdout);
#endifscanf("%d%d", &n, &m);For(i, 1, n){scanf("%s", rs + 1);For(j, 1, m)if(rs[j] == '.') mp[i][j] = 1, ex = i, ey = j;}PlugDp();printf("%lld\n", ans);return 0;
}这篇关于[Ural1519] Formula 1的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


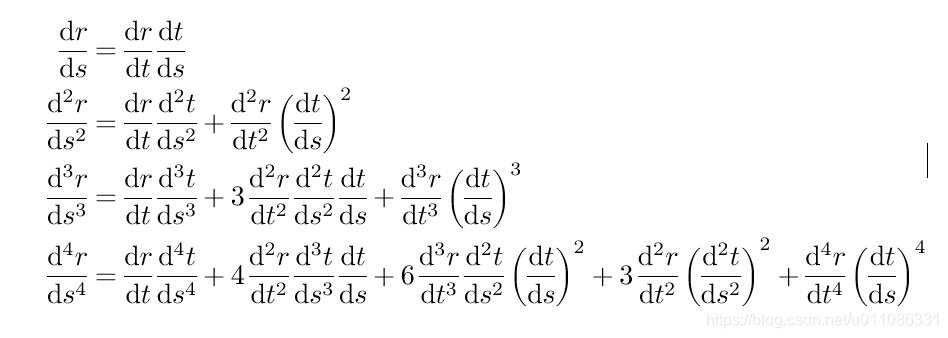


![插头DP讲解+[BZOJ1814]:Ural 1519 Formula 1(插头DP)](https://img2018.cnblogs.com/blog/1714305/201907/1714305-20190730061301729-1733822808.png)
