相关文章
服务容错(Service Fault Tolerance)
服务容错(Service Fault Tolerance)是微服务架构中确保系统在部分服务出现故障时仍能继续运行的能力。容错机制的目标是提升系统的鲁棒性和可用性,防止单点故障扩散影响整个系统。以下是一些常见的服务容错机制和最佳实践。 1. 熔断器模式(Circuit Breaker Pattern) 熔断器模式是一种保护系统免受部分服务故障影响的技术。当某个服务出现故障或响应缓慢时,熔断器会快
在浮点数比较时使用容差范围,而不是直接比较两个数值是否完全相等
浮点数运算可能会引入微小的误差,这是由计算机在表示和处理浮点数时所使用的有限精度所导致的。为了理解这一点,以下是一些关键原因: 1. 浮点数的有限精度: 二进制表示:浮点数在计算机中是以二进制的形式存储的。然而,并不是所有的十进制小数都能被精确地转换为二进制小数。例如,像 0.1 这样的十进制数在二进制中不能被精确表示,而是以一个近似值存储。这就会引入一些舍入误差。有限位数:浮点数在计算机中有
Apache Flink数据流的Fault Tolerance机制
简介 Apache Flink提供了一个失败恢复机制来使得数据流应用可以持续得恢复状态。这个机制可以保证即使线上环境的失败,程序的状态也将能保证数据流达到exactly once的一致性。注意这里也可以选择降级到保证at least once的一致性级别。 失败恢复机制持续地构建分布式流式数据的快照。对于那些只有少量状态的流处理应用,这些快照都是非常轻量级的并且可以以非常频繁的频率来构建快照而
Flink1.4 Fault Tolerance源码解析-1
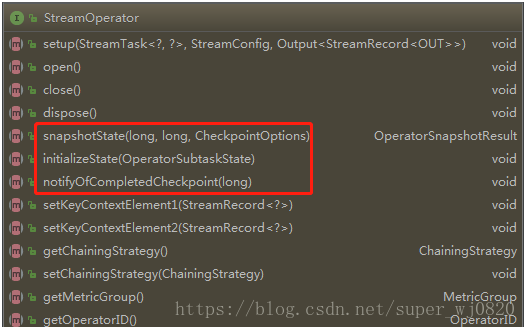
前言:本篇关注Flink,对Fault Tolerance的源码实现进行阐述,主要介绍Api层及Flink现有实现。 本篇文章重点关注以下问题: 具备Fault Tolerance能力的两种对象:Function和Operator分析两个接口,列举典型实现,并做简要分析 1. 具备Fault Tolerance能力的两种对象 Function Operator 1.1 Functi
MATLAB知识点:uniquetol函数(★★☆☆☆)考虑了一定的容差的unique函数
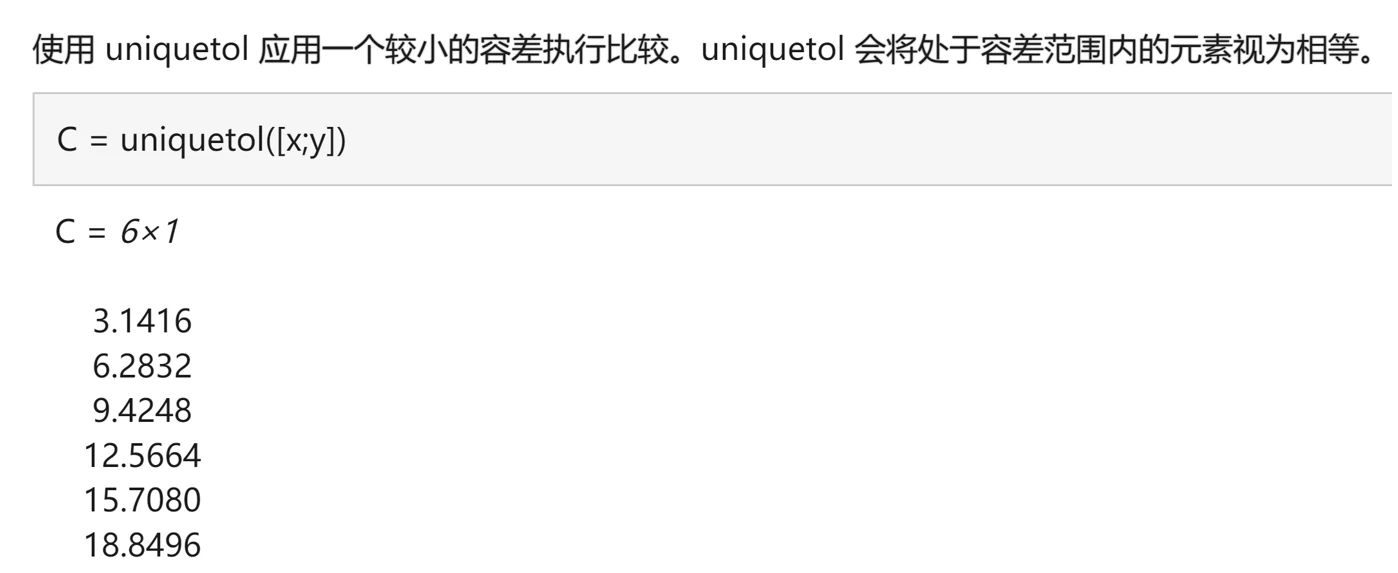
讲解视频:可以在bilibili搜索《MATLAB教程新手入门篇——数学建模清风主讲》。 MATLAB教程新手入门篇(数学建模清风主讲,适合零基础同学观看)_哔哩哔哩_bilibili 节选自第3章:课后习题讲解中拓展的函数 在讲解第三章课后习题的过程中,我给大家拓展了一些讲义中没有介绍的新函数: (10)uniquetol函数(★★☆☆☆) uniquetol函数和uni
【0250】深入分析Write-Ahead Log Fault Tolerance(WAL容错)
文章目录 1. 前言2. 容错2.1 缓存(Caching)2.2 数据损坏(Data Corruption)2.3 非原子写(Non-Atomic Writes) 1. 前言 本文将详细讲解影响 2. 容错 不言而喻,预写式日志必须保证在任何情况下都能恢复崩溃(除非持久性存储本身被破坏)。影响数据一致性的因素有很多,但我将只讨论最重要的几个:缓存、数据损坏和非原子写。
SYD881X使用代码修改32.768khz tolerance PPM
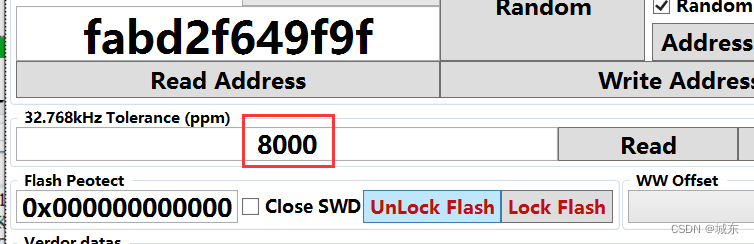
32.768khz tolerance PPM的功能和效果参考文章:https://chengdong.blog.csdn.net/article/details/118540241对于使用外部32.768khz的代码ppm使用2000是比较合适的,但是当代码使用内部32.768khz的时候ppm为2000就不合适了,这个值要在6000以上,建议使用8000,但是当代码使用的是内部32.768k
ADS仿真 之 容差/良率分析
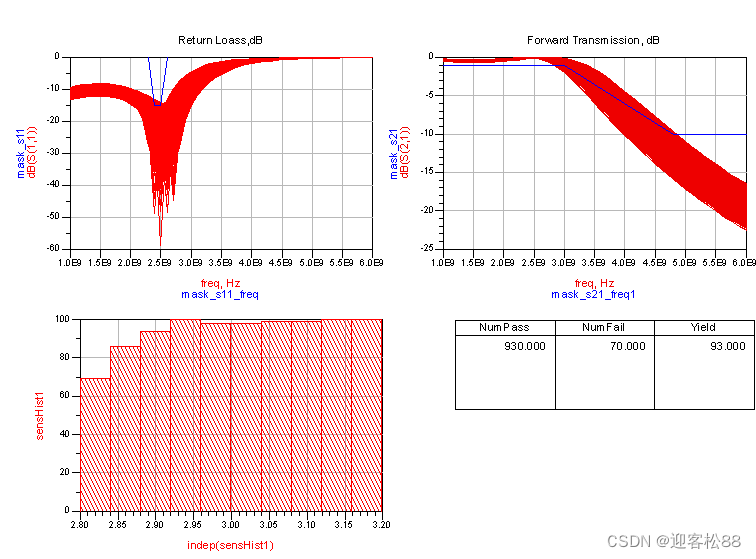
之所以要进行容差分析, 是因为任何电子元器件均存在一定的误差, 如电感、电容的精度等。 例如一个标称为2.0nH±0.1nH的电感,代表的意思产品有99.74%的概率落在2.0nH±0.1nH范围内, 即满足6σ ,σ是标准偏差或者说方差,当产品随机变量值与平均值之差为6σ时,产品的良品率为99.74%,这是统计学范畴。 一、容差分析 电路模块的容差分析可以通过