吴恩达Deep Learning编程作业 Course1-神经网络和深度学习-第三周作业

吴恩达Deep Learning编程作业 Course1-神经网络和深度学习-第三周作业

Planar data classification with one hidden layer具有一个隐藏层的平面数据分类

编程目的：

• 使用带有非线性激活函数，比如tanh函数，实现一个具有单隐藏层的二分类神经网络。
• 计算交叉熵代价。
• 实现前向传播和反向传播。

1.需要使用的包

1.numpy：是Python用于科学计算的基本包。
2.matplotlib：python用于画图的库。
3.sklearn：为数据挖掘和数据分析提供简单有效的工具。
4.planar_utils：提供了在这个任务中使用的各种有用的函数。（吴恩达老师作业中提供）
5.testCases：提供了一些测试示例来评估函数的正确性

2.数据集

本次编程使用的数据集为"flower"。按照常规，我们首先加载数据集，查看以下数据集的信息。
代码：

import numpy as np
import matplotlib.pyplot as plt
from Utils import planar_utils, sigmoidif __name__ == "__main__":X, Y = planar_utils.load_planar_dataset()print(X.shape)print(Y.shape)plt.scatter(X[0, :], X[1, :], c=np.squeeze(Y), s=40, cmap=plt.cm.Spectral)

运行结果：


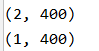
从运行结果可以看出X的维数是（2，400），Y的维数是（1，400）。也就是说X有400个样本，每个样本有两个特征。
在图像中红色的样本点的标签是Y=0，蓝色的样本点的标签是Y=1。

3.简单的逻辑回归

在构建完整的神经网络之前，让我们先看看逻辑回归在这个问题上的表现。可以使用sklearn的内置函数来实现这一点。运行下面的代码来训练数据集上的逻辑回归分类器。

    clf = sklearn.linear_model.LogisticRegressionCV()clf.fit(X.T, Y.T)

运行结果：会打印出两个警告，我们暂时忽略这两个warning。
D:\programfile\Anaconda3\lib\site-packages\sklearn\utils\validation.py:724: DataConversionWarning: A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples, ), for example using ravel().
y = column_or_1d(y, warn=True)
D:\programfile\Anaconda3\lib\site-packages\sklearn\model_selection_split.py:1978: FutureWarning: The default value of cv will change from 3 to 5 in version 0.22. Specify it explicitly to silence this warning.
warnings.warn(CV_WARNING, FutureWarning)

把逻辑回归分类器绘制出来：
代码：

 clf = sklearn.linear_model.LogisticRegressionCV()clf.fit(X.T, Y.T)# 绘制决策边界plot_decision_boundary(lambda x: clf.predict(x), X, Y)plt.title("Logistic Regression")#打印准确率LR_predictions = clf.predict(X.T)print('逻辑回归模型正确标记准确率：%d' %float((np.dot(Y, LR_predictions) + np.dot(1 - Y, 1 - LR_predictions)) / float(Y.size) * 100) + '%')

运行结果：


从上述运行结果我们也可以看出sklearn中自带的逻辑回归模型并不能很好的对数据集中的数据进行分类，正确率还不到50%。我们的目的就是得到更好的分类模型，接下来我们一起实现这个神经网络模型。

4.神经网络模型。

现在我们尝试着训练一个只有一层隐藏层的神经网络。
模型如图所示：

数学公式运算理解：
以一个样本$x^{(}i)$为例：
$z^{[1](i)}$ = $W^{[1]}{x}^{(1)}$ + $b^{[1](i)}$
$a^{[1](i)}$ = $\tanh (z^{[1](i)})$
$z^{[2](i)}$ = $W^{[2]}{a}^{[1](i)}$ + $b^{[2](i)}$
${\hat{y}}^{(i)}$ = $a^{[1](i)}$ = $\sigma (z^{[2](i)})$
$y_{prediction}^{(i)}$ = $\{\begin{array}{l}0,a^{[2](i)}>0.5\\ 1\end{array}$
根据样本的预测结果，我们可以计算代价，以下为代价函数公式：
$$J=-\frac{1}{m}\sum _{i=0}^m\left(y^{(i)}\log \left(a^{[2](i)}\right)+(1-y^{(i)})\log \left(1-a^{[2](i)}\right)\right)$$

4.1模型设计

建立一般神经网络模型的方法：
1.定义神经网络结构。
2.初始化模型参数。
3.循环：

• 实现前向传播
• 计算损失
• 反向传播获得梯度
• 更新参数

4.2 定义神经网络结构

定义三个变量：

• n_x:输入层的大小
• n_h:隐藏层的大小(设置为4)
• n_y:输出层的大小

先定义函数layer_sizes_test_cases，主要用来自动生成训练样本，代码如下：

def layer_sizes_test_case():#随机生成不同的训练集X和标签集Y#使用random.randrange()方法X_feature_num = random.randrange(1, 9)Y_feature_num = random.randrange(1, 3)number = random.randrange(10, 100)#(特征数，样本个数）X_assess = np.zeros(shape=(X_feature_num, number))Y_assess = np.zeros(shape=(Y_feature_num, number))return X_assess, Y_assess

定义layer_sizes函数，根据训练集和标签集获得输入层、隐藏层、输出层大小：

def layer_sizes(X, Y):n_x = X.shape[0]n_h = 4n_y = Y.shape[0]return n_x, n_h, n_y

测试：

X_assess, Y_assess = layer_sizes_test_case()n_x, n_h, n_y = layer_sizes(X_assess, Y_assess)print("输入层大小：n_x = %d"%n_x)print("隐藏层大小：n_h = %d"%n_h)print("输出层大小：n_y = %d"%n_y)

运行结果：

4.3 初始化模型参数

使用np.random.randn(a,b) * 0.01随机初始化形状矩阵(a,b)。将偏差向量初始化为零（乘以0.01的原因是：权重过大会使得输入激活函数的值过大，进而造成梯度下降停滞；randn生成随机数的范围是[0, 1)）。
使用np.zeros((a,b))初始化一个带0的形状矩阵(a,b)。
代码：

def initiallize_parameters(n_x, n_h, n_y):np.random.seed(2)W1 = np.random.randn(n_h, n_x) * 0.01b1 = np.zeros(shape = (n_h, 1))W2 = np.random.randn(n_y, n_h) * 0.01b2 = np.zeros(shape=(n_y, 1))assert (W1.shape == (n_h, n_x))assert (b1.shape == (n_h, 1))assert (W2.shape == (n_y, n_h))assert (b2.shape == (n_y, 1))parameters = {"W1": W1,"b1": b1,"W2": W2,"b2": b2}return parameters

测试：

 X_assess, Y_assess = layer_sizes_test_case()n_x, n_h, n_y = layer_sizes(X_assess, Y_assess)print("输入层大小：n_x = %d"%n_x)print("隐藏层大小：n_h = %d"%n_h)print("输出层大小：n_y = %d"%n_y)parameters = initiallize_parameters(n_x, n_h, n_y)print("W1 = " + str(parameters["W1"]))print("b1 = " + str(parameters["b1"]))print("W2 = " + str(parameters["W2"]))print("b2 = " + str(parameters["b2"]))

运行结果：

4.3 单隐层神经网络的实现

1.前向传播

代码：

def forward_propagation(X, parameters):print(X.shape)W1 = parameters['W1']b1 = parameters['b1']W2 = parameters['W2']b2 = parameters['b2']Z1 = np.dot(W1, X) + b1 #4,2 2,1 = 4,1A1 = np.tanh(Z1) #4, 1Z2 = np.dot(W2, A1) + b2 #1, 4 4,1 = 1,1A2 = sigmoid.sigmoid(Z2) #1, 1print(A2.shape)assert(A2.shape == (1, X.shape[1]))cache = {"Z1" : Z1,"A1" : A1,"Z2" : Z2,"A2" : A2}return A2, cache

测试：（用到的函数附在文档结尾处）

	X_assess, parameters = forward_propagation_test_case()A2, cache = forward_propagation(X_assess, parameters)print("Z1 = " + str(cache['Z1']))print("A1 = " + str(cache['A1']))print("Z2 = " + str(cache['Z2']))

运行结果：

2.代价函数

进行完前向传播后下一步我们就要计算代价，计算公式如下：
$$J=-\frac{1}{m}\sum _{i=0}^m(y^{(i)}\log \left(a^{[2](i)}\right)+(1-y^{(i)})\log \left(1-a^{[2](i)}\right))$$

代码：

def compute_cost(A2,Y,parameters):m = Y.shape[1]W1 = parameters['W1']W2 = parameters['W2']#对应元素相乘logprobs = np.multiply(np.log(A2), Y) + np.multiply(np.log(1 - A2), (1 - Y))cost = -np.sum(logprobs)/mcost = np.squeeze(cost)assert (isinstance(cost, float))return cost

运行结果:

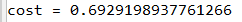
3.计算反向传播

利用前向传播得到的cache里面的数据进行计算。
下面我们来看一下反向传播的计算公式：

在前向传播中我们使用的第一个激活函数是sigmoid，其导数可以写成
$g^{{}^{\prime }}$(z) = $g(z)(1-g(z))$；第二个激活函数是tanh，其导数为$g^{{}^{\prime }}$(z) = $(1-g(z{)}^2)$；

实现代码：

def backward_propagation(parameters, cache, X, Y):m = X.shape[1]W1 = parameters['W1']W2 = parameters['W2']A1 = cache['A1']A2 = cache['A2']dZ2 = A2 - YdW2 = np.dot(dZ2, A1.T)#纵轴之和db2 = np.sum(dZ2, axis=1, keepdims=True)/mdZ1 = np.multiply(np.dot(W2.T, dZ2), 1 - np.power(A1, 2))dW1 = np.dot(dZ1, X.T)/mdb1 = (1 / m) * np.sum(dZ1, axis=1, keepdims=True)grads = {"dW1": dW1,"db1": db1,"dW2": dW2,"db2": db2}return grads

调用代码：

parameters, cache, X_assess, Y_assess = backward_propagation_test_case()grads = backward_propagation(parameters, cache, X_assess, Y_assess)print("dW1 = " + str(grads["dW1"]))print("db1 = " + str(grads["db1"]))print("dW2 = " + str(grads["dW2"]))print("db2 = " + str(grads["db2"]))

运行结果：

4.更新参数

现在我们已经得到了dW1,dW2,db1,db2的值，我们可以使用这些利用梯度下降法进行参数更新。
一般进行梯度更新的公式:$\theta =\theta -\alpha \frac{\alpha J}{\alpha \theta }$，其中$\alpha$是学习率，$\theta$是参数。
梯度下降算法具有良好的学习速率(收敛)和较差的学习速率(发散)。图片由Adam Harley提供。


代码实现：

def update_parameters(parameters, grads, learning_rate = 1.2):W1 = parameters['W1']b1 = parameters['b1']W2 = parameters['W2']b2 = parameters['b2']dW1 = grads['dW1']db1 = grads['db1']dW2 = grads['dW2']db2 = grads['db2']W1 = W1 - learning_rate * dW1b1 = b1 - learning_rate * db1W2 = W2 - learning_rate * dW2b2 = b2 - learning_rate * db2parameters = {"W1": W1,"b1": b1,"W2": W2,"b2": b2}return parameters

测试：

 parameters, grads = update_parameters_test_case()parameters = update_parameters(parameters, grads)print("W1 = " + str(parameters["W1"]))print("b1 = " + str(parameters["b1"]))print("W2 = " + str(parameters["W2"]))print("b2 = " + str(parameters["b2"]))

运行结果：

这里我们已更新完了参数，实际上我们更新完的参数可能并不是最优参数，我们需要多次迭代，指导满足一定的条件，这样才能最大可能性的得到最优参数。接下来我们就将上述步骤整合起来。

5.整合上述过程

实现代码：

def nn_model(X, Y, n_h, num_iterations = 10000, print_cost = False):#1.获得各层单元个数np.random.seed(3)n_x, nh, n_y = layer_sizes(X, Y)#2.初始化参数parameters = initiallize_parameters(n_x, n_h, n_y)W1 = parameters['W1']b1 = parameters['b1']W2 = parameters['W2']b2 = parameters['b2']#3.循环实现整个计算过程i = 0while i < num_iterations:i+=1print(i)#1.前向传播A2, cache = forward_propagation(X, parameters)#2.计算代价cost = compute_cost(A2, Y, parameters)#3.反向传播grads = backward_propagation(parameters, cache, X, Y)#4.更新参数parameters = update_parameters(parameters, grads)if print_cost and i % 1000 == 0:print("第%i次计算得到的代价为：%f." %(i, cost))return parameters

测试：

X_assess, Y_assess = nn_model_test_case()parameters = nn_model(X_assess, Y_assess, 4, num_iterations = 10000, print_cost=False)print("W1 = " + str(parameters["W1"]))print("b1 = " + str(parameters["b1"]))print("W2 = " + str(parameters["W2"]))print("b2 = " + str(parameters["b2"]))

运行结果：

6.预测

接下来我们就可以构建函数来进行模型的预测了。
$y_{prediction}^{(i)}$ = $\{\begin{array}{l}0,a^{[2](i)}>0.5\\ 1\end{array}$
代码：

def predict(parameters, X):A2, cache = forward_propagation(X, parameters)#返回浮点数x的四舍五入值。>0.5为1 <=0.5为0predict_result = np.round(A2)return predict_result

测试：

parameters, X_assess = predict_test_case()predictions = predict(parameters, X_assess)print("predictions mean = " + str(np.mean(predictions)))

运行结果：

7. 运行整个模型查看结果：

代码：

X, Y = planar_utils.load_planar_dataset()parameters = nn_model(X, Y, 4, 1000, print_cost=True)plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)plt.title("Decision Boundary for hidden layer size " + str(4))

运行结果：

对比一开始我们使用逻辑回归模型进行划分，现在的结果明显优于逻辑回归模型的分类结果。

7. 计算精度

代码：

predictions = predict(parameters, X)print('Accuracy: %d' % float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100) + '%')

运行结果：

8. 测试不同隐藏层单元数下的预测精度

代码：
运行结果：


从结果看出，在这个问题上隐藏层设置为5会得到最高的预测率。
同时我们也可以改变学习率，看看最终的结果。

7. 运行其他数据集

代码：

 noisy_circles, noisy_moons, blobs, gaussian_quantiles, no_structure = load_extra_datasets()datasets = {"noisy_circles": noisy_circles,"noisy_moons": noisy_moons,"blobs": blobs,"gaussian_quantiles": gaussian_quantiles}dataset = "noisy_moons"X, Y = datasets[dataset]print(X.shape)print(Y.shape)X, Y = X.T, Y.reshape(1, Y.shape[0])if dataset == "blobs":Y = Y % 2plt.scatter(X[0, :], X[1, :], c=np.squeeze(Y), s=40, cmap=plt.cm.Spectral)parameters = nn_model(X, Y, n_h=5, num_iterations=5000)plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)predictions = predict(parameters, X)print('Accuracy: %d' % float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100) + '%')

运行结果：



大家可以自己再进行学习率或隐藏层单元数等相关参数的调整。

Reference：https://github.com/Kulbear/deep-learning-coursera/blob