Python 全栈体系【四阶】（十二）

本文主要是介绍Python 全栈体系【四阶】（十二），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

第四章 机器学习

十五、朴素贝叶斯

朴素贝叶斯是一组功能强大且易于训练的分类器，它使用贝叶斯定理来确定给定一组条件的结果的概率，“朴素”的含义是指所给定的条件都能独立存在和发生。朴素贝叶斯是多用途分类器，能在很多不同的情景下找到它的应用，例如垃圾邮件过滤、自然语言处理等。

1. 概率

1.1 定义

概率是反映随机事件出现的可能性大小。随机事件是指在相同条件下，可能出现也可能不出现的事件。例如：

（1）抛一枚硬币，可能正面朝上，可能反面朝上，这是随机事件。正/反面朝上的可能性称为概率；

（2）掷骰子，掷出的点数为随机事件。每个点数出现的可能性称为概率；

（3）一批商品包含良品、次品，随机抽取一件，抽得良品/次品为随机事件。经过大量反复试验，抽得次品率越来越接近于某个常数，则该常数为概率。

我们可以将随机事件记为 A 或 B，则 P（A）, P（B）表示事件 A 或 B 的概率。

1.2 联合概率与条件概率

1.2.1 联合概率

指包含多个条件且所有条件同时成立的概率，记作$P(A,B)$ ，或$P(AB)$，或$P(A\bigcap B)$

1.2.2 条件概率

已知事件 B 发生的条件下，另一个事件 A 发生的概率称为条件概率，记为：$P(A|B)$ p(下雨|阴天)

1.2.3 事件的独立性

事件 A 不影响事件 B 的发生，称这两个事件独立，记为：

$$P(AB)=P(A)P(B)$$

因为 A 和 B 不相互影响，则有：

$$P(A|B)=P(A)$$

可以理解为，给定或不给定 B 的条件下，A 的概率都一样大。

1.3 先验概率与后验概率

1.3.1 先验概率

先验概率也是根据以往经验和分析得到的概率，例如：在没有任何信息前提的情况下，猜测对面来的陌生人姓氏，姓李的概率最大（因为全国李姓为占比最高的姓氏），这便是先验概率。

1.3.2 后验概率

后验概率是指在接收了一定条件或信息的情况下的修正概率，例如：在知道对面的人来自“牛家村”的情况下，猜测他姓牛的概率最大，但不排除姓杨、李等等，这便是后验概率。

1.3.3 两者的关系

事情还没有发生，求这件事情发生的可能性的大小，是先验概率（可以理解为由因求果）。事情已经发生，求这件事情发生的原因是由某个因素引起的可能性的大小，是后验概率（由果求因）。先验概率与后验概率有不可分割的联系，后验概率的计算要以先验概率为基础。

2. 贝叶斯定理

2.1 定义

贝叶斯定理由英国数学家托马斯.贝叶斯 (Thomas Bayes)提出，用来描述两个条件概率之间的关系，定理描述为：

$$P(A|B)=\frac{P(A)P(B|A)}{P(B)}$$

其中，$P(A)$和$P(B)$是 A 事件和 B 事件发生的概率。$P(A|B)$称为条件概率，表示 B 事件发生条件下，A 事件发生的概率。推导过程：

$$\begin{gathered} P(A,B)=P(B)P(A|B) \\ P(B,A)=P(A)P(B|A) \end{gathered}$$

其中$P(A,B)$称为联合概率，指事件 B 发生的概率，乘以事件 A 在事件 B 发生的条件下发生的概率。因为$P(A,B)=P(B,A)$, 所以有：

$$P(B)P(A|B)=P(A)P(B|A)$$

两边同时除以 P(B)，则得到贝叶斯定理的表达式。其中，$P(A)$是先验概率，$P(A|B)$是已知 B 发生后 A 的条件概率，也被称作后验概率。

2.2 贝叶斯定理示例

【示例一】计算诈骗短信的概率

事件	概率	表达式
所有短信中，诈骗短信	5%	P（A）= 0.05
所有短信中，含有“中奖”两个字	4%	P（B）= 0.04
所有短信中，是诈骗短信，并且含有“中奖”两个字	50%	P(B|A) = 0.5

求：收到一条新信息，含有“中奖”两个字，是诈骗短信的概率？

$P(A|B)=P(A)P(B|A)/P(B)=0.05\ast 0.5/0.04=0.625$

【示例二】计算喝酒驾车的概率

事件	概率	表达式
所有客人中，驾车	20%	P（A）= 0.2
所有客人中，喝酒	10%	P（B）= 0.1
所有客人中，开车并且喝酒	5%	P（B|A）= 0.05

求：喝过酒仍然会开车的人的比例是多少？

$P(A|B)=P(A)P(B|A)/P(B)=0.2\ast 0.05/0.1=0.1$

【示例三】

假设一个学校中 60%的男生 和 40%的女生

女生穿裤子的人数和穿裙子的人数相等

所有的男生都穿裤子，一个人随机在远处眺望，看一个穿裤子的学生。

请问这个学生是女生的概率：

p(女) = 0.4

p(裤子|女) = 0.5

p(裤子) = 0.8

P(女|裤子) = 0.4 * 0.5 / 0.8 = 0.25

$$P(A|B)=\frac{P(A)P(B|A)}{P(B)}$$

3. 朴素贝叶斯分类器

3.1 分类原理

朴素贝叶斯分类器就是根据贝叶斯公式计算结果进行分类的模型，“朴素”指事件之间相互独立无影响。例如：有如下数据集：

Text	Category
A great game（一个伟大的比赛）	Sports（体育运动）
The election was over（选举结束）	Not sports（不是体育运动）
Very clean match（没内幕的比赛）	Sports（体育运动）
A clean but forgettable game（一场难以忘记的比赛）	Sports（体育运动）
It was a close election（这是一场势均力敌的选举）	Not sports（不是体育运动）

求：”A very close game“ 是体育运动的概率？数学上表示为 P(Sports | a very close game)​。根据贝叶斯定理，是运动的概率可以表示为：

$$P(Sports|averyclosegame)=\frac{P(averyclosegame|sports)\ast P(sports)}{P(averyclosegame)}$$

不是运动概率可以表示为：

$$P(NotSports|averyclosegame)=\frac{P(averyclosegame|Notsports)\ast P(Notsports)}{P(averyclosegame)}$$

概率更大者即为分类结果。由于分母相同，即比较分子谁更大即可。我们只需统计”A very close game“ 多少次出现在 Sports 类别中，就可以计算出上述两个概率。但是”A very close game“ 并没有出现在数据集中，所以这个概率为 0，要解决这个问题，就假设每个句子的单词出现都与其它单词无关（事件独立即朴素的含义），所以，P(a very close game)可以写成：

$$P(averyclosegame)=P(a)\ast P(very)\ast P(close)\ast P(game)$$

$$\begin{gathered} P（averyclosegame|Sports)= \\ P(a|Sports)\ast P(very|Sports)\ast P(close|Sports)\ast P(game|Sports) \end{gathered}$$

统计出“a", “very”, “close”, "game"出现在"Sports"类别中的概率，就能算出其所属的类别。

具体计算过程如下：

• 第一步：计算总词频：Sports 类别词语总数 11，Not Sports 类别词语总数 9

• 第二步：计算每个类别的先验概率

  # Sports和Not Sports概率
  P(Sports) = 3 / 5 = 0.6
  P(Not Sports) = 2 / 5 = 0.4# Sports条件下各个词语概率
  P(a | Sports) = (2 + 1) / (11 + 14) = 0.12
  P(very | Sports) = (1 + 1) / (11 + 14) = 0.08
  P(close | Sports) = (0 + 1) / (11 + 14) = 0.04
  P(game | Sports) = (2 + 1) / (11 + 14) = 0.12# Not Sports条件下各个词语概率
  P(a | Not Sports) = (1 + 1) / (9 + 14) = 0.087
  P(very | Not Sports) = (0 + 1) / (9 + 14) = 0.043
  P(close | Not Sports) = (1 + 1) / (9 + 14) =  = 0.087
  P(game | Not Sports) = (0 + 1) / (9 + 14) = 0.043
  

  其中，分子部分加 1，是为了避免分子为 0 的情况；分母部分都加了词语总数 14，是为了避免分子增大的情况下计算结果超过 1 的可能。

• 第三步：将先验概率带入贝叶斯定理，计算概率：

  • 是体育运动的概率：

    $$\begin{gathered} P（averyclosegame|Sports)= \\ P(a|Sports)\ast P(very|Sports)\ast P(close|Sports)\ast P(game|Sports)= \\ 0.12\ast 0.08\ast 0.04\ast 0.12=0.00004608 \end{gathered}$$

    • 不是体育运动的概率：

  $$\begin{gathered} P（averyclosegame|NotSports)= \\ P(a|NotSports)\ast P(very|NotSports)\ast P(close|NotSports)\ast P(game|NotSports)= \\ 0.087\ast 0.043\ast 0.087\ast 0.043=0.000013996 \end{gathered}$$

  • 分类结果：P(Sports) = 0.00004608 , P(Not Sports) = 0.000013996， 是体育运动。

3.2 实现朴素贝叶斯分类器

在 sklearn 中，提供了三个朴素贝叶斯分类器，分别是：

• GaussianNB（高斯朴素贝叶斯分类器）：适合用于样本的值是连续的，数据呈正态分布的情况（比如人的身高、城市家庭收入、一次考试的成绩等等）
• MultinominalNB（多项式朴素贝叶斯分类器）：适合用于大部分属性为离散值的数据集
• BernoulliNB（伯努利朴素贝叶斯分类器）：适合用于特征值为二元离散值或是稀疏的多元离散值的数据集

该示例中，样本的值为连续值，且呈正态分布，所以采用 GaussianNB 模型。代码如下：

# 朴素贝叶斯分类示例
import numpy as np
import sklearn.naive_bayes as nb
import matplotlib.pyplot as mp# 输入，输出
x, y = [], []# 读取数据文件
with open("../data/multiple1.txt", "r") as f:for line in f.readlines():data = [float(substr) for substr in line.split(",")]x.append(data[:-1])  # 输入样本：取从第一列到倒数第二列y.append(data[-1])  # 输出样本：取最后一列x = np.array(x)
y = np.array(y, dtype=int)# 创建高斯朴素贝叶斯分类器对象
model = nb.GaussianNB()
model.fit(x, y)  # 训练# 计算显示范围
left = x[:, 0].min() - 1
right = x[:, 0].max() + 1buttom = x[:, 1].min() - 1
top = x[:, 1].max() + 1grid_x, grid_y = np.meshgrid(np.arange(left, right, 0.01),np.arange(buttom, top, 0.01))mesh_x = np.column_stack((grid_x.ravel(), grid_y.ravel()))
mesh_z = model.predict(mesh_x)
mesh_z = mesh_z.reshape(grid_x.shape)mp.figure('Naive Bayes Classification', facecolor='lightgray')
mp.title('Naive Bayes Classification', fontsize=20)
mp.xlabel('x', fontsize=14)
mp.ylabel('y', fontsize=14)
mp.tick_params(labelsize=10)
mp.pcolormesh(grid_x, grid_y, mesh_z, cmap='gray')
mp.scatter(x[:, 0], x[:, 1], c=y, cmap='brg', s=80)
mp.show()

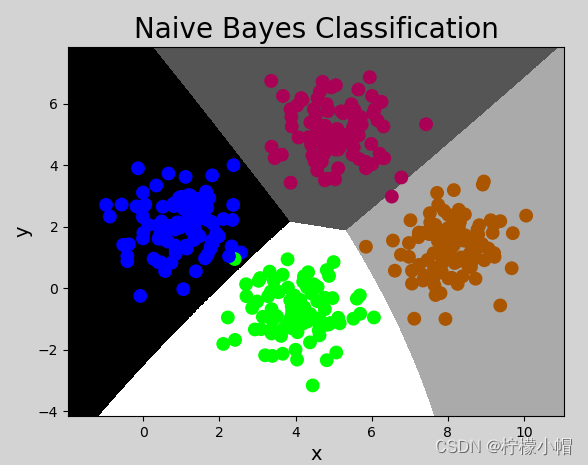
执行结果：

4. 总结

4.1 什么是朴素贝叶斯

朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。“朴素”的含义为：假设问题的特征变量都是相互独立地作用于决策变量的，即问题的特征之间都是互不相关的。

4.2 朴素贝叶斯分类的特点

4.2.1 优点

• 逻辑性简单
• 算法较为稳定。当数据呈现不同的特点时，朴素贝叶斯的分类性能不会有太大的差异。
• 当样本特征之间的关系相对比较独立时，朴素贝叶斯分类算法会有较好的效果。

4.2.2 缺点

• 特征的独立性在很多情况下是很难满足的，因为样本特征之间往往都存在着相互关联，如果在分类过程中出现这种问题，会导致分类的效果大大降低。

4.3 什么情况下使用朴素贝叶斯

根据先验概率计算后验概率的情况，且样本特征之间独立性较强。

这篇关于Python 全栈体系【四阶】（十二）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---