本文主要是介绍【网络安全】【密码学】【北京航空航天大学】实验三、数论基础(下)【C语言实现】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
实验三、数论基础(下)
一、实验内容
1、中国剩余定理(Chinese Remainder Theorem)
(1)、算法原理
m1, m2, … mk 是一组两两互素的正整数,且 M = m1 · m2 · … · mk 为它们的乘积, 则如下的同余方程组:
x == a1 (mod m1)
x == a2 (mod m2)
…
x == ak (mod mk)
对于模M有唯一的解 x = (M · e1 · a1 / m1 + M · e2 · a2 / m2 + … + M · ek · ak / mk) (mod M)
其中 ei 满足 M / mi · ei == 1(mod mi)
(2)、算法流程
本算法的大致流程如下图所示:
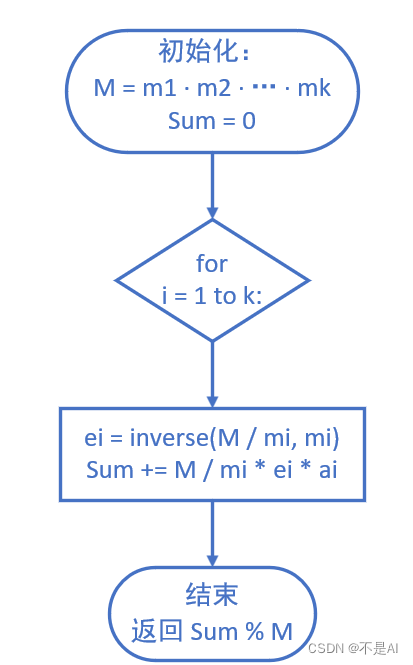
(3)、算法的代码实现(C语言)
#include <stdio.h>int reverse(int k, int m); // 函数,返回k模m的逆元int main()
{int i;int r; // 方程组中的方程个数 (不能超过100)int b[100]; // 余数数组int m[100]; // 模数数组int mul = 1;int M[100]; // M数组int M1[100]; // M'数组int x = 0; // 方程组的根// printf("%d", reverse(3, 7)); // 一行测试代码printf("请输入方程的个数:");scanf_s("%d", &r); // 选用安全的输入函数,避免可能的栈溢出(攻击)printf("请输入 %d 个余数,之间以空格分隔:", r);for(i = 0;i < r;i ++){scanf("%d", &b[i]);}printf("请输入 %d 个模数,之间以空格分隔:", r);for(i = 0;i < r;i ++){scanf("%d", &m[i]);mul *= m[i];}for(i = 0;i < r;i ++){M[i] = mul / m[i];}for(i = 0;i < r;i ++){M1[i] = reverse(M[i], m[i]);}for(i = 0;i < r;i ++){x += M1[i] * M[i] * b[i];}x %= mul;printf("此同余方程组的解(模%d)是:", mul);printf("%d", x);return 0;
}int reverse(int k, int m)
{int i;for(int i = 1;i < m;i ++){if(k * i % m == 1){return i;}}return -1;
}
(4)、算法测试
测试点1:
x == 1 (mod 4)
x == 2 (mod 5)
x == 3 (mod 7)
运行时截图:
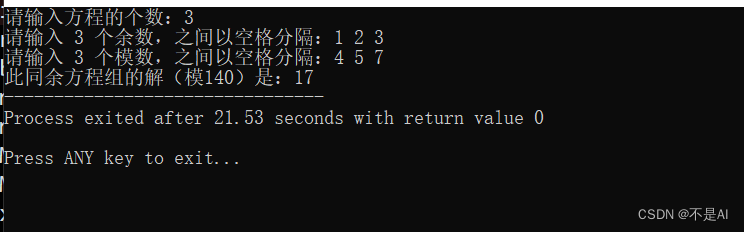
解为 x == 17 (mod 140)
测试点2:
x == 7 (mod 23)
x == 9 (mod 28)
x == 16 (mod 33)
运行时截图:
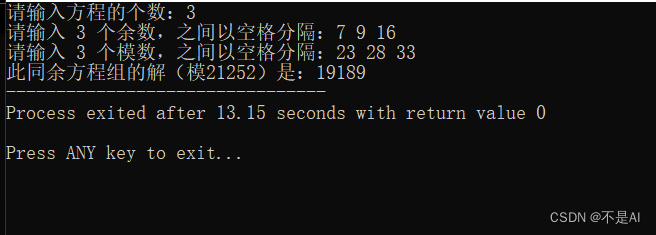
解为 x == 19189 (mod 21252)
测试点3:
x == 23 (mod 283)
x == 28 (mod 102)
x == 33 (mod 35)
运行时截图:

解为 x == 43888 (mod 1010310)
2、素性检测算法(Miller-Rabin’s Test for Primality)
(1)、算法原理
根据费马小定理,设 p 是素数,a 为整数,且满足 (a, p) = 1, 则满足 a ^ (p - 1) = 1 (mod p), 以及二次探测定理:如果 p 是一个素数,且 0 < x < p, 且同余方程 x ^ 2 = 1 (mod p) 成立,那么 x = 1 或x = p - 1。米勒·拉宾 Miller-Rabin 素性检测算法是基于以上两个定理的随机化算法,用于判断一个整数是合数还是素数。
(2)、算法流程
本算法的大致流程如下图所示:

(3)、算法的代码实现(C语言)
#include <stdio.h>
#include <stdlib.h>typedef long long unsigned LLU;
typedef int BOOL;#define TRUE 1
#define FALSE 0// 长整数快速模乘算法
LLU quickMult(LLU a, LLU b, LLU c)
{LLU result = 0;while(b > 0) {if(b & 1)result = (result + a) % c;a = (a + a) % c;b >>= 1;}return result;
}// 长整数快速幂取模算法
LLU quickPower(LLU a, LLU b, LLU c)
{LLU result = 1;while(b > 0) {if(b & 1)result = quickMult(result, a, c);a = quickMult(a, a, c);b >>= 1;}return result;
}// 米勒·拉宾素性检验算法(单次测试)
BOOL MillerRabinPrimeTest(LLU n)
{LLU d, x, newX, a = 1;int i;for (i = 0; i < 4; i ++)a *= rand();a = a % (n - 3) + 2; // 随机地选取一个a∈[2,n-2]int s = 0; // s为d中的因子2的幂次数。d = n - 1;while ((d & 1) == 0) { // 将d中的因子2全部提取出来。s ++;d >>= 1;}x = quickPower(a, d, n);for (i = 0; i < s; i ++) { // 进行s次二次探测newX = quickPower(x, 2, n);if (newX == 1 && x != 1 && x != n - 1)return FALSE; // 用二次定理的逆否命题,此时n被确定为合数。x = newX; }if (x != 1)return FALSE; // 用费马小定理的逆否命题判断,此时x=a^(n-1) (mod n),那么n确定为合数。return TRUE; //用费马小定理的逆命题判断。能经受住考验至此的数,大概率为素数。
}//经过连续特定次数的Miller-Rabin测试后,
//如果返回值为TRUE表示n为素数,返回值为FALSE表示n为合数。
BOOL isPrimeByMR(LLU n)
{if((n & 1) == 0)return FALSE;int i;for (i = 0; i < 100; i ++)if(MillerRabinPrimeTest(n) == FALSE)return FALSE;return TRUE;
}// 主函数
int main()
{LLU n;printf("请输入待判断素性的整数:");scanf("%lld", &n);BOOL result;result = isPrimeByMR(n);printf("\n------判断中......------\n\n");if(result == TRUE)printf("%llu 是素数", n);elseprintf("%llu 是合数", n);return 0;
}
(4)、算法测试
测试点1:
判断1000023是素数还是合数。(答:合数)
运行时截图:
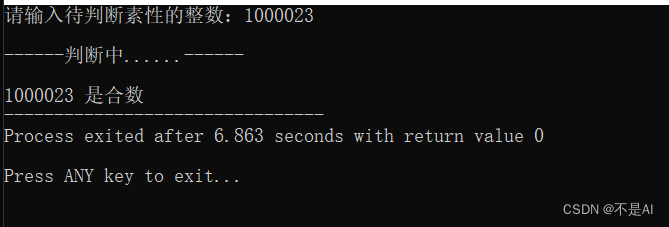
测试点2:
判断1000033是素数还是合数。(答:素数)
运行时截图:

测试点3:
判断100160063是素数还是合数。(答:合数)
运行时截图:
 测试点4:
测试点4:
判断1500450271是素数还是合数。(答:素数)
运行时截图:
说明:算法为概率性判断,即可能将合数错判为素数(对计算机来说,已在极短的时间内完成了100次重复的MR测试,故该错判的概率极低),但绝无可能将素数错判为合数。
二、参考文献
1、《密码编码学与网络安全——原理与实践(第七版)》(Cryptography and Network Security, Principles and Practice, Seventh Edition),【美】威廉 斯托林斯 William Stallings 著,王后珍等 译,北京,电子工业出版社,2017年12月。
2、《密码学实验教程》,郭华 刘建伟等 主编,北京,电子工业出版社,2021年1月。
这篇关于【网络安全】【密码学】【北京航空航天大学】实验三、数论基础(下)【C语言实现】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







