本文主要是介绍建堆的时间复杂度计算,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
公式及结果
原理解释
公式推导
公式及结果
以最坏情况来计算建堆的时间复杂度,假设该堆为满二叉树,堆高为h。i为第i层,设第i层高度为hi,第i层结点数位ni,堆的复杂度为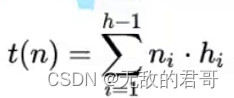
i = 1 ,直到 i = h-1 结束。将 1 到 h - 1 的 n1*h1 +..... ni*hi 相加。
t(n) = O(N)。
原理解释
图仅为解释时间复杂度计算,实际建堆为由下向上。先建地基,再盖高楼,逐层往上。
每层的每个结点都要向下执行当前的高度次。
直到倒数第二层的每个结点执行完一次结束。
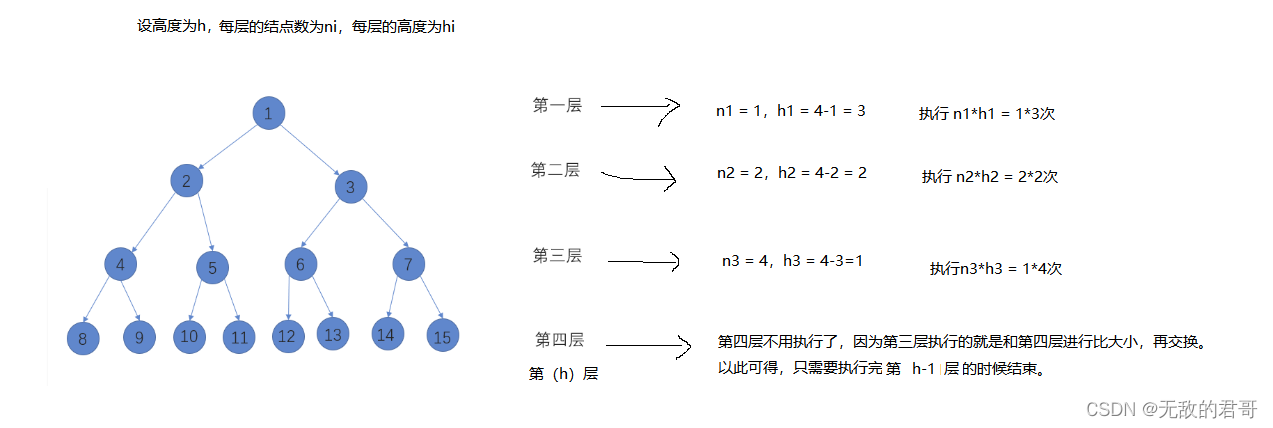
图中 h 为 4 。
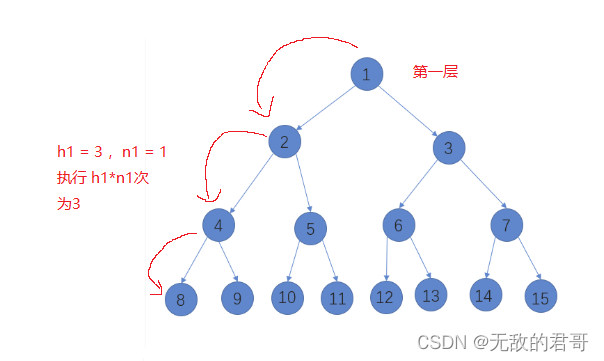
第一层到最底层的高度为 h1 = 3,有一个结点 n1 = 1,相乘就是第一层执行的次数。
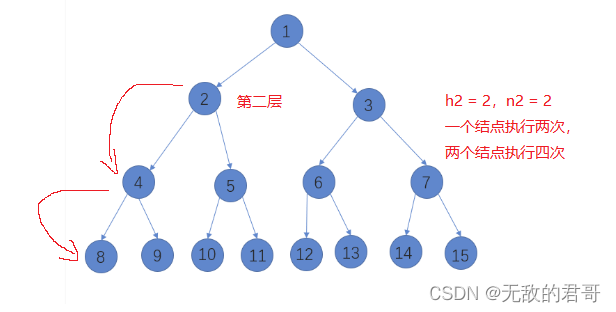
第二层到最底层的高度为 h2 = 2 ,有两个结点 n2 = 2,相乘就是第二层执行的次数。
只需执行到 当 hi = 1时,可结束。也就是说 第 h-1 层的高度 就是 hi = 1。第一张图中有解释。
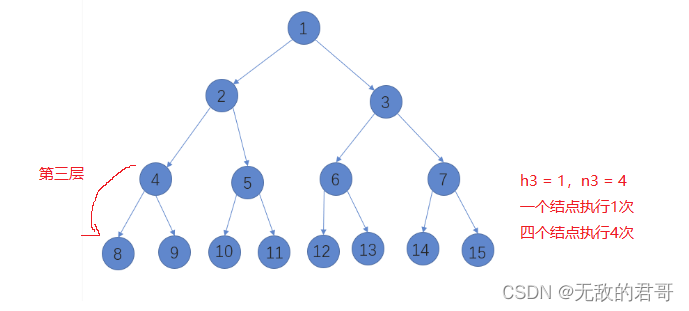
最坏的情况下则需要第i层的每个节点向下,和该结点的大孩子或者小的孩子进行交换,执行到第 h-1 层结束。
将每层执行的次数相加就是建堆的时间复杂度。
公式推导
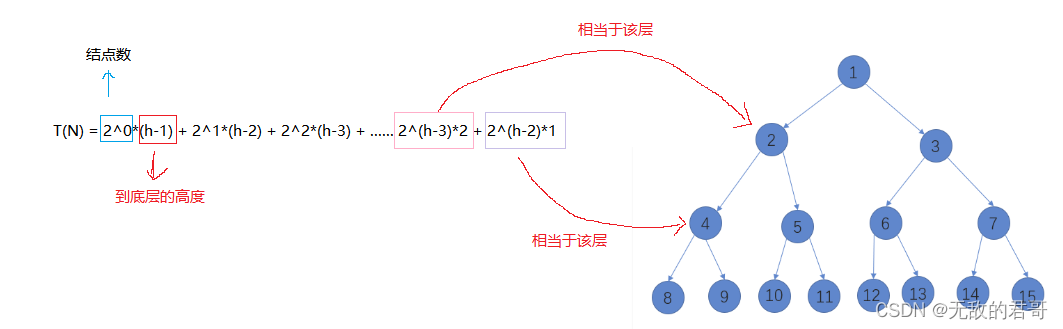
错位相减法。
将T(N)乘2再减去T(N)。

T(N) = N - log2N
因为O(log2N)的时间复杂度比O(N)低,所以忽略O(log2N)。
可得建堆的时间复杂度为O(N)。
这篇关于建堆的时间复杂度计算的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




