本文主要是介绍二叉树面试题(三)--将搜索二叉树转为有序的双向链表、对称二叉树、另一棵树的二叉树和判断二叉树,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.将搜索二叉树转为有序的双向链表
给定一棵搜索二叉树,试将它转为双向链表。
二叉搜索树的特点是:它的中序遍历是有序的。
本题的思路其实就是根据中序遍历,依次取下根结点,然后处理根结点。对根结点的处理,就是设置该结点的前后引用。对结点的处理:
//处理根private static Node prev=null;private static Node head=null;private static void buildDList(Node node) {node.left=prev;if(prev!=null){prev.right=node;}else{head=node;}prev=node;}
package com.xunpu.datastruct.tree;public class Test1 {public static class Node{char val;//值Node left;//左子树Node right;//右子树Node(char val){this.val=val;}}//将二叉搜索树转为有序的双向链表private static void inOrderSearchTree(Node root){if(root!=null){inOrderSearchTree(root.left);//处理根结点buildDList(root);inOrderSearchTree(root.right);}}//处理根private static Node prev=null;private static Node head=null;private static void buildDList(Node node) {node.left=prev;if(prev!=null){prev.right=node;}else{head=node;}prev=node;}private static Node searchTreeToSortedList(Node root){prev=null;head=null;inOrderSearchTree(root);return head;}private static Node buildSearchTree(){Node a=new Node('A');Node b=new Node('B');Node c=new Node('C');Node d=new Node('D');Node e=new Node('E');Node f=new Node('F');Node g=new Node('G');Node h=new Node('H');e.left=b;e.right=g;b.left=a;b.right=d;d.left=c;g.left=f;g.right=h;return e;}public static void main(String[] args) {Node root = buildSearchTree();Node head=searchTreeToSortedList(root);for(Node cur=head;cur!=null;cur=cur.right){System.out.print(cur.val);}}
}
2.对称二叉树
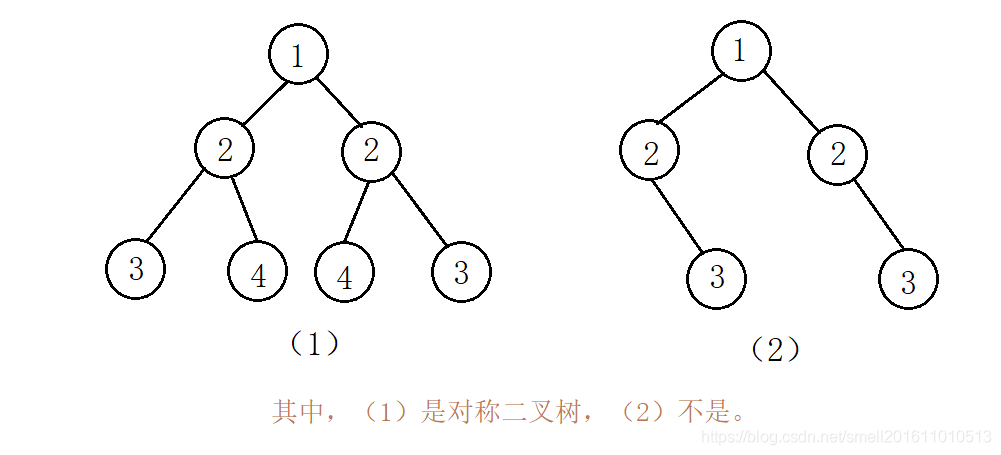
思路:空树和只有一个结点的树为对称二叉树。首先判断根结点是否为空,然后再判断再判断它的左右子树是否是镜像二叉树。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode(int x) { val = x; }* }*/
class Solution {public boolean isSymmetric(TreeNode root) {if(root==null){return true;}if(root.left==null&&root.right==null){return true;}return isMirror(root.left,root.right);}private static boolean isMirror(TreeNode p,TreeNode q){if(p==null&&q==null){//必要!!!return true;}if(p==null||q==null){return false;}if(p.val==q.val){return isMirror(p.left,q.right)&&isMirror(p.right,q.left);}else{return false;}}
}3.另一棵树的子树
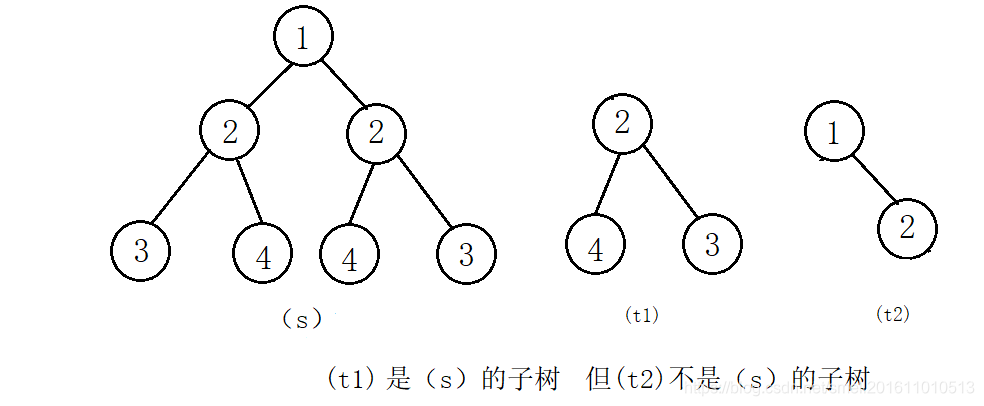
思路:其实是判断两棵树是否相同。先判断s树是否和t树相同,然后在s的左子树中查找是否和t树相同;如果不相同,则直接返回和s的右子树比较的结果。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode(int x) { val = x; }* }*/
class Solution {public boolean isSubtree(TreeNode s, TreeNode t) {return find(s,t);}//查找t的根结点是否在s中private static boolean find(TreeNode s,TreeNode t){if(s==null){return false;}//判断根这棵树是否和t树相同if(isSame(s,t)){return true;}//在根的左子树中查找t树if(find(s.left,t)){return true;}//如果在左子树中没有找到,就在右子树中找。return find(s.right,t);}//判断两棵树是否相同private static boolean isSame(TreeNode p,TreeNode q){if(p==null&&q==null){return true;}if(p==null||q==null){return false;}return p.val==q.val&&isSame(p.left,q.left)&&isSame(p.right,q.right);}
}4.判断是否是平衡二叉树
思路:如果根结点为空,则是平衡二叉树;然后依次判断左子树和右子树是否为平衡二叉树,是,则继续判断;不是则直接返回。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode(int x) { val = x; }* }*/
class Solution {public boolean isBalanced(TreeNode root) {if(root==null){return true;}if(!isBalanced(root.left)){return false;}if(!isBalanced(root.right)){return false;}int left=getLength(root.left);int right=getLength(root.right);if((left-right)>=-1&&(left-right)<=1){return true;}return false;}//求树的高度private int getLength(TreeNode root){if(root==null){return 0;}int left=getLength(root.left);int right=getLength(root.right);return (left>right?left:right)+1; }
}
这篇关于二叉树面试题(三)--将搜索二叉树转为有序的双向链表、对称二叉树、另一棵树的二叉树和判断二叉树的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


