空间数据索引RTree（R树）完全解析及Java实现

本文是在https://www.cnblogs.com/cmi-sh-love/p/kong-jian-shud-ju-suo-yinRTree-wan-quan-jie-xi-jiJa.html?share_token=e5b096d7-6dbf-4839-9992-b29913335ba9基础上进行修改和补充的。

第一部分 空间数据的背景介绍

空间数据的建模

基于实体的模型（基于对象）Entity-based models (or object based)

• 0-dimensional objects : 一般使用点point来表示那些对于不需要使用到形状信息的实体。
• 1-dimensional objects or linear objects: 用于表示一些路网的边，一般用于表示道路road。 (polyline)
• 2-dimensional objects or surfacic objects: 用于表示有区域面积的实体。 (polygon)
• 3-dimensional objects or voxel objects:用于表示有空间体积的实体。(polytope）

常用的空间数据查询方式

• 窗口查询：给定一个查询窗口（通常是一个多维矩形，二维为矩形，3维为长方体），返回查询窗口所覆盖包围的物体。



• 点查询：给定一个点，返回包含这个点的所有几何图形。

空间数据的表示方法

key:最小限定矩形、限定框

通常，我们不选择去索引几何物体本身，而是采用最小限定箱MBB（minimum bounding box ) 作为不规则几何图形的key来构建空间索引（类似B树中的key是数轴上的一个点，以该点的值作为key，二维的R树就是以矩形作为key，三维的R树就是以立方体作为Key，R树检索的是key，所以这点务必要搞清楚，不要把指针当成了key）。

• 在二维的情况下，我们称之为最小限定矩形。MBR(minimum bounding retangle)
  

• 三维的情况下，我们称最小限定箱MBB(minimum bounding box)
  

如何搜索key（矩形或者立方体等）

通过索引操作对象的MBB（后面将MBR和MBB不做区分，除非指明维数）来进行查询一共分为两步：

• Filtering: 过滤掉MBB不相交的数据集，剩下的MBB组成一个超集（下图中红色为待查找MBB，橙色是与之有交集的MBB）。实际上，这个超集从某一层的某个节点开始，其中的多个entry可能满足条件，而这些entry指向的下一层的node中也可能有多个满足条件，所以后续的查找可能需要对超集中的所有子树及叶子节点进行遍历。
  

• Refinement: 计算实际的几何形状会不会满足查询条件，精确化。
  ·

如何用数据表示一个MBR（MBB）

通常，我们只需要两个点就可限定一个矩形，也就是矩形某个对角线的两个点就可以决定一个唯一的矩形。通常我们使用（左下，右上两个点表示）或者使用右上左下，都是可以的（原则上是越简单也好，或者元组的越小越好）。三维可以用底面的左下角、底面的右上角、顶面的左上角三元组表示。

     　　　　　　

• 表示一个点的数据：

public class Point{ //用一个类来表示一个点public Float x;public Float y
}

• 表示一个MBR的数据

public class MBR{public Point BottomLeft;public Point TopRight;
}

判断如何判断key是否有交集 

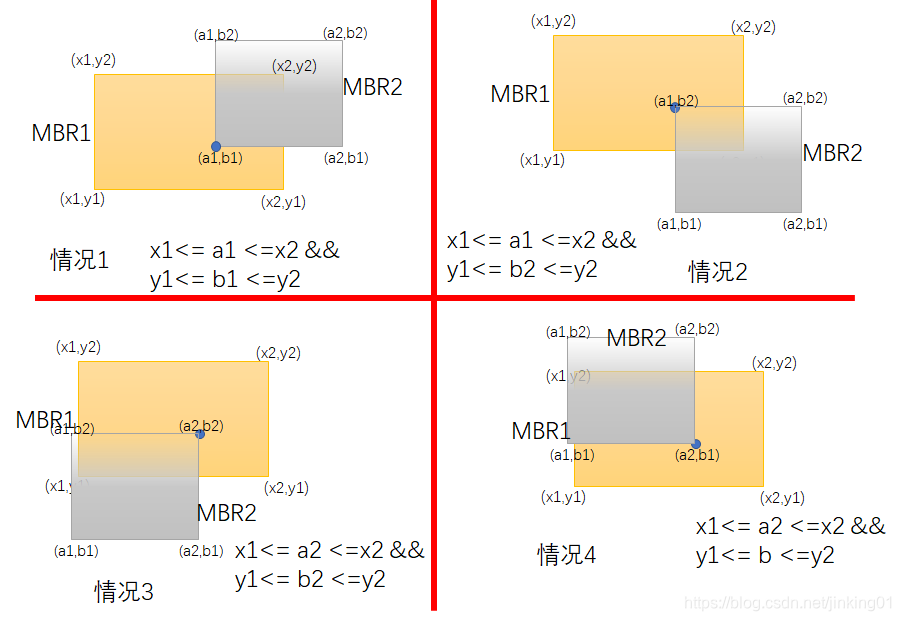
因为B树表示的是一维数轴，所以key的的判断用的是等号（=），因为是个点，但是在二维或者高维空间是一片区域或者空间，却无法用等号，而是要考虑相交。如何判断两个MBR是否相交？

如果一个MBR的任何一个顶点的坐标（MBR2的左下角(x3,y3)）位于另一个MBR（MBR1）的xRange和yRangle里面，则说明这两个MBR相交。对于3维空间来说，则要判断8个顶点。

                    

R树

对于B/B+树，由于它的线性特点，通常用来索引一维数据。（比它大的往一边走，比它小的往一边走，但只是在一个维度下进行比较）。B树是一棵平衡树，它是把一维直线分为若干段线段，当我们查找满足某个要求的点的时候，只要去查找它所属的线段即可。这种思想其实就是先找一个大的空间，再逐步缩小所要查找的空间，最终在一个自己设定的最小不可分空间内找出满足要求的解。一个典型的B树查找如下：




要查找某一满足条件的点，先去找到满足条件的线段，然后遍历所在线段上的点，即可找到答案。B树是一种相对来说比较复杂的数据结构，尤其是在它的删除与插入操作过程中，因为它涉及到了叶子结点的分解与合并。

R树的简介

B树是解决低纬度数据（通常一维，也就是一个数据维度上进行比较），R树很好的解决了这种高维空间搜索问题。它把B树的思想很好的扩展到了多维空间，采用了B树分割空间的思想（如果B树在一维的线段进行分割，R树就是在二维甚至多维度的空间），并在添加、删除操作时采用合并、分解结点的方法，保证树的平衡性。因此，R树就是一棵用来存储高维数据的平衡树。


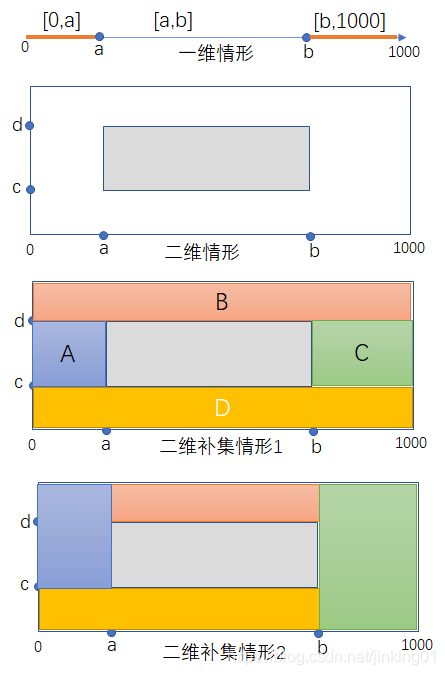
我们说过，B树是采用切分线段来缩小数据查询范围的一种思想，我们又说了，R树是b树的多维版，以及R树也采用了B树的这一种分割的思想，那么，如果说线段的分割是一维的分割（一维空间的分割容易表示，线段[a,b]之外的“区域”表示很简单[0,a],[a,1000]。在B树中，一维的表示具有排他性，每一个点都只能处于某一个叶子节点中，且只能被唯一的内部节点中的唯一的entry表示，其补集是唯一的，且表示比较简单，在对B树进行调整时也不会太复杂。但是，在R 树中，它一维却允许存在交叉，这样，效率肯定没有B树好。具体见下面的案例和描述）。

那二维的分割就应该是区域的分割（但某个区域A之外的“区域”表示起来就非常麻烦，因为你无法用于与区域A的表达形式相同的方式进行表达，比如，区域A=((20,20),(100,100)）是左下角为（20,20），右上角为（100,100）的矩形区域，但是在整个空间（比如设定为((0,0),(1000,1000)）中，其补集虽然是唯一的，但是表示却不是唯一的（如下图所示），或者说，至少得用4个区域来表示其补集，这个虽然能表示，但是对于不停的插入新的区域到R树中，为了做到所有的区域之间没有重叠，可能需要不断的调整整棵树，带来非常大的调整开销（不是不能做，而是相对于一维的情形的成本太高），所以一般的R树中各个矩形框是允许交叉重叠的。

而三维的就是几何空间的分割了，其补集表示起来更加复杂，需要6个长方体来表示其补集，每插入一个节点，带来的调整开销会更大。

要注意的是R树并不只是二维空间数据的索引而已，它还可以索引三维甚至更高维。

一个三维的R树


此外R树还可以退化成一维，但是分割的线段存在重叠问题，效果不如B树。


R树的数据结构

如上所述，R树是B树在高维空间的扩展，是一棵平衡树。每个R树的叶子结点包含了多个指向不同数据的指针，这些数据可以是存放在硬盘中的，也可以是存在内存中。

根据R树的这种数据结构，当我们需要进行一个高维空间查询时，我们只需要遍历少数几个叶子结点所包含的指针（即缩小到某个区域下去进行查询，还是采用缩小范围的思想），查看这些指针指向的数据是否满足要求即可。这种方式使我们不必遍历所有数据即可获得答案，效率显著提高。下图是R树的一个简单实例：




解释一下这张图。

• 首先我们假设所有数据都是二维空间下的几何形状，图中仅仅标志了R8，R9，R10区域中的数据（形状所代表的物体），其他的叶子节点仅仅用MBB表示。为了实现R树结构，我们用一个最小边界矩形恰好框住这个不规则区域，这样，我们就构造出了一个区域：R8。R8的特点很明显，就是正正好好框住所有在此区域中的数据。其他实线包围住的区域，如R9，R10，R11等都是同样的道理。这样一来，我们一共得到了12个最最基本的最小矩形。这些矩形都将被存储在子结点中。
• 下一步操作就是进行高一层次的处理。我们发现R8，R9，R10三个矩形距离最为靠近，因此就可以用一个更大的矩形R3恰好框住这3个矩形。
• 同样道理，R15，R16被R6恰好框住，R11，R12被R4恰好框住，等等。所有最基本的最小边界矩形被框入更大的矩形中之后，再次迭代，用更大的框去框住这些矩形。

用地图的例子来解释，就是所有的数据都是餐厅所对应的地点，先把相邻的餐厅划分到同一块区域，划分好所有餐厅之后，再把邻近的区域划分到更大的区域，划分完毕后再次进行更高层次的划分，直到划分到只剩下两个最大的区域为止。要查找的时候就方便了。

下面就可以把这些大大小小的矩形存入我们的R树中去了。根结点存放的是两个最大的矩形，这两个最大的矩形框住了所有的剩余的矩形，当然也就框住了所有的数据。下一层的结点存放了次大的矩形，这些矩形缩小了范围。每个叶子结点（R8--R19）都是存放的最小的矩形，这些矩形中可能包含有n个数据。

上图表达的是一个很理想的案例，如果待搜索区域与R8、R12、R16都有交叉，那么搜索路径就不会像上图那样是一条单路径了。

因此，在R树中搜索每个区域或者点并不像B树那样一次就能确定，而是可能需要多次遍历。原因就是因为R树中的MBB是允许交叉的，当查询某个点或者某个区域时，因为该点或者区域可以与多个entry表示的区域有重叠，只有有重叠，就需要遍历该entry所指向的内部节点或者叶子节点。也就是说，对于搜索点或者区域，在R树中，它的搜索路径是一棵树，它包含多条路径。但在B树中，对于每一个点的搜索，是单一的一条路径。

以餐厅为例，假设我要查询广州市天河区天河城附近一公里的所有餐厅地址怎么办？

• 打开地图（也就是整个R树），先选择国内还是国外（也就是根结点）。
• 然后选择华南地区（对应第一层结点），选择广州市（对应第二层结点），
• 再选择天河区（对应第三层结点），
• 最后选择天河城所在的那个区域（对应叶子结点，存放有最小矩形），遍历所有在此区域内的结点，看是否满足我们的要求即可。

R树的查找规则跟查地图很像吧？对应下图：



一个更具体的使用场景

假设我们有一个地图路网要进行道路的快速索引，那么我们可以将每一条路的最小MBB作为R树的数据单元来进行构建R树。


每一条路使用一个最小MBB来进行包裹，使它成为R树的叶子结点（也就是那些数据结点）（路是各种弯道，所以为每条路构建一个MBB，最后就是一大堆密密麻麻的有大量交叉的矩形）


（这里采用的是R树的改进版本R*树）然后对于建立起来的R树（图中浅灰色的矩形不太清晰，但每一个都表示一条路）再进行查找道路的使用就可以使用我们那种“缩小范围”的查找思想。从上往下一层一层查找。


一棵R树满足如下的性质：

• 1. 除非它是根结点之外，所有叶子结点包含有m至M个记录索引（条目）。作为根结点的叶子结点所具有的记录个数可以少于m。通常，m=M/2。
• 2. 对于所有在叶子节点中存储的记录（条目,entry），I是最小的可以在空间中完全覆盖这些记录所代表的点的矩形（注意：此处所说的“矩形”是可以扩展到高维空间的）。
• 3. 每一个非叶子结点拥有m至M个孩子结点，除非它是根结点。
• 4. 对于在非叶子结点上的每一个条目，i是最小的可以在空间上完全覆盖这些条目所代表的点的矩形（同性质2）。
• 5. 所有叶子结点都位于同一层，因此R树为平衡树。

R树的操作

搜索

R树的搜索操作很简单，跟B树上的搜索十分相似。它返回的结果是所有符合查找信息的记录条目。而输入是什么？输入不仅仅是一个范围了，它更可以看成是一个空间中的矩形。也就是说，我们输入的是一个搜索矩形。
先给出伪代码：

Function：Search
描述：假设T为一棵R树的根结点，查找所有搜索矩形S覆盖的记录条目。

• S1:[查找子树] 如果T是非叶子结点：（1）如果T所对应的矩形与S有重合，那么检查所有T中存储的条目，对于所有这些条目，使用Search操作作用在每一个条目所指向的子树的根结点上（即T结点的孩子结点）；（2）如果T所对应的矩形和S没有重合，则返回。
• S2:[查找叶子结点] 如果T是叶子结点：（1）如果T所对应的矩形与S有重合，那么直接检查T所指向的所有记录条目，然后返回符合条件的记录；（2）如果T所对应的矩形和S没有重合，则返回。

我们通过下图来理解这个Search操作。



红色查询区域S和绿色的P3子树和P4子树相重叠，所以根据“缩小空间”的思想，只需要遍历P3和P4所在子树就行而无需遍历P1，P2.（有个问题，P3、P4的I在哪里存着？图中P1-P4都是节点P的entry，P中有I表示4个entry的MBB，但是entry中是否有各自指向的节点的I呢？）

插入

R树的插入操作也同B树的插入操作类似。当新的数据记录需要被添加入叶子结点时，若叶子结点溢出，那么我们需要对叶子结点进行分裂操作。显然，叶子结点的插入操作会比搜索操作要复杂。插入操作需要一些辅助方法才能够完成。
插入操作的伪代码：（疑问：entry的数据结构是啥？）

【Function：Insert】
描述：将新的记录条目E插入给定的R树中。

• I1：[为新记录找到合适插入的叶子结点]开始ChooseLeaf方法选择叶子结点L以放置记录E。
• I2：[添加新记录至叶子结点] 如果L有足够的空间来放置新的记录条目，则向L中添加E。如果没有足够的空间，则进行SplitNode方法以获得两个结点L与LL，这两个结点包含了所有原来叶子结点L中的条目与新条目E。
• I3：[将变换向上传递] 开始对结点L进行AdjustTree操作（调整I的大小，如果L的I变了，其父节点的I肯定也变化了），如果进行了分裂操作，那么同时需要对LL进行AdjustTree操作。
• I4：[对树进行增高操作] 如果因为L结点的分裂向上传播导致了根结点的分裂，那么需要创建一个新的根结点，并且让它的两个孩子结点分别为原来那个根结点分裂后的两个结点。

选择合适的叶子节点以插入新的entry的伪代码：

【Function：ChooseLeaf】
描述：选择叶子结点以放置新条目E。
- CL1：[Initialize]设置N为根结点。
- CL2：[叶子结点的检查] 如果N为叶子结点，则直接返回N。
- CL3：[选择子树] 如果N不是叶子结点，则遍历N中所有条目，找出添加E.I时扩张最小的条目，并把该条目指向的结点定义为F。如果有多个这样的条目，那么选择面积最小的条目指向的节点。
- CL4：[下降至叶子结点] 将F置为新的N，从CL2开始重复操作。

叶子节点中插入entry后可能导致I发生变化，而后可能会影响到其父节点直到根节点的I，其调整向上传导过程伪代码：

【Function：AdjustTree】
描述：叶子结点的I的改变向上传递至根结点以改变各个矩形。

• AT1：[初始化] 将N为当前要处理的叶子节点L。
• AT2：[检验是否完成] 如果N为根结点，则停止操作。
• AT3：[调整父结点条目的最小边界矩形] 设P为N的父节点，EN为指向在父节点P中指向N的条目。调整EN.I以保证所有在N中的矩形都被恰好包围。（从这里看出，entry中是包含了两项的，1个是ptr指向子节点，一个是I，而node中只有这些entry，并没有单独的一个I来表示所有entry的I的MBB）
• AT4：[向上传递结点分裂] 如果N有一个刚刚被分裂产生的结点NN，则创建一个指向NN的条目ENN。如果P有空间来存放ENN，则将ENN添加到P中。如果没有，则对P进行SplitNode操作以得到P和PP。
• AT5：[升高至下一级] 如果N等于L且发生了分裂，则把NN置为PP。从AT2开始重复操作。

• 有足够的空间插入的情况，由于插入的x所在的区域P2的数据条目仍然有足够的空间容纳条目x，且x的区域面积即MBR也位于区域P2之内，所以这种情况下，我们认为P2拥有足够的插入空间（同时P2的范围不需要调整，因此P2 的父节点不需要处理）。



• 需要增大MBR的插入情况，由于插入的y所在的区域P2的数据条目仍然有足够的空间容纳条目y，但是y的区域面积即MBR并不完全位于P2的区域之内，因此我们在插入数据y后会导致P2区域的相应扩大，这个时候因为P2没有父节点，所以不用处理，如果P2有父节点，则还需要更新父节点中指向P2的那个entry的I，同时计算更新后的I是否会引起上一层节点中的entry 的I发生变化。



• 需要进行分裂的插入情况，由于插入的w所在的区域P1的数据条目已经没有足够的空间容纳条目w，因为假设我们定义R树的阶m=4，而区域P1已经容纳了四个条目「A，B，C，K」了，插入w后孩子数为5，以及超过m=4了，所以要进行分裂操作，来保证树的平衡性。



采用分裂算法（下面会进行介绍）对结点（或者说区域）P1进行合理地分裂。使其分裂成P1（包含A，B）和P5（包含K，C，W）两个结点。并且需要向上传递这种分裂。由于分裂之后原来根结点「P1，P2，P3，P4」变成了「P1，P2，P3，P，P5」，因此根结点的孩子数由4变成5，超过了阶数m=4.所以根结点要（采用我们的分裂算法）进行分裂，分裂成Q1（包含P1，P5，P2）和Q2（包含P3，P4）两个结点，由于此时分裂已经传递到根结点，所以生成新的根结点记录Q1，Q2。



如何合理地分裂到两个组（原则上讲，应该考虑各种组合方式，然后选择划分后重叠区域最小或者面积之和最小的划分方式，但这种穷举的方式开销比较大，且即时选择了当前分裂效果最好的方式，也只是当前的局部最优）



挑选种子有多个方法，这里Quadratic（二次方）方案，对于所有条目中所有entry，任意选两个E1和E2，计算可以包裹着E1，E2的最小限定框J=MBR(E1, E2) ，然后计算增量d= J-E1-E2.计算结束后选择d最大的一对（即增量最大）。（这里为什么要这样呢：之所以要挑选d最大的一对，是因为如果d较大，说明挑选出来的两对条目基于对角线离得比较远，这样的好处就是分裂后的两个分组可以尽量不重叠）。然后以这俩entry为种子，再分别围绕种子选择矩形框，构成两个集合。





挑选出seed1和seed2之后，就将剩下的要分配的分裂条目分个这两个seed使它们各称为一个组。而这个分配的原则就是离谁比较“近”就和谁一组。这里的“近”指的是任何一个条目MBB–E和seed1、seed2分别计算可以包裹着E和seed1的最小限定框J1=MBR(E，seed1)， 可以包裹着E和seed2的最小限定框J2=MBR(E，seed2)。再分别计算增量d1=J1-E-seed1，d2=J2-E-seed2。d1，d2哪个小就说明哪个“近”。



所以分裂的具体情况还是很复杂的，真想不懂这些大神怎么会想得到这些。除了上述Quadratic的分裂算法之外还有其他的分裂算法，如下图中间图，但是分裂的效果都不如R*树（R树的改进版）的算法好（R*树的分裂计算方式不是计算出2个种子，而是计算了整个节点的MBR中心点到其所含有的所有entry的MBR的中心点的距离，然后进行排序，前面的x%保留下来，后面的(1-x)%的entry要重新插入到整棵R树中，在重新插入过程中，会尽可能的把这些entry放到更合适的位置，也就是说进行了重新平衡。所以，R*的分裂方式效果可能是最好的，但是代价比较大，特别是对于基于磁盘的R树。）。




删除

R树的删除操作与B树的删除操作会有所不同，不过同B树一样，会涉及到压缩等操作。相信读者看完以下的伪代码之后会有所体会。R树的删除同样是比较复杂的，需要用到一些辅助函数来完成整个操作。
伪代码如下：

【Function：Delete】
描述：将一条记录E从指定的R树中删除。
D1：[找到含有记录的叶子结点] 使用FindLeaf方法找到包含有记录E的叶子结点L。如果搜索失败，则直接终止。
D2：[删除记录] 将E从L中删除。
D3：[传递记录] 对L使用CondenseTree操作
D4：[缩减树] 当经过以上调整后，如果根结点只包含有一个孩子结点，则将这个唯一的孩子结点设为根结点。

【Function：FindLeaf】
描述：根结点为T，期望找到包含有记录E的叶子结点。
FL1：[搜索子树] 如果T不是叶子结点，则检查每一条T中的条目F，找出与E所对应的矩形相重合的F（不必完全覆盖）。对于所有满足条件的F，对其指向的孩子结点进行FindLeaf操作，直到寻找到E或者所有条目均以被检查过。
FL2：[搜索叶子结点以找到记录] 如果T是叶子结点，那么检查每一个条目是否有E存在，如果有则返回T。

【Function：CondenseTree】
描述：L为包含有被删除条目的叶子结点。如果L的条目数过少（小于要求的最小值m），则必须将该叶子结点L从树中删除。经过这一删除操作，L中的剩余条目必须重新插入树中。此操作将一直重复直至到达根结点。同样，调整在此修改树的过程所经过的路径上的所有结点对应的矩形大小。
CT1：[初始化] 令N为L。初始化一个用于存储被删除结点包含的条目的链表Q。
CT2：[找到父条目] 如果N为根结点，那么直接跳转至CT6。否则令P为N 的父结点，令EN为P结点中存储的指向N的条目。
CT3：[删除下溢结点] 如果N含有条目数少于m，则从P中删除EN，并把结点N中的条目添加入链表Q中。
CT4：[调整覆盖矩形] 如果N没有被删除，则调整EN.I使得其对应矩形能够恰好覆盖N中的所有条目所对应的矩形。
CT5：[向上一层结点进行操作] 令N等于P，从CT2开始重复操作。
CT6：[重新插入孤立的条目] 所有在Q中的结点中的条目需要被重新插入。原来属于叶子结点的条目可以使用Insert操作进行重新插入，而那些属于非叶子结点的条目必须插入删除之前所在层的结点，以确保它们所指向的子树还处于相同的层。

R树删除记录过程中的CondenseTree操作是不同于B树的。我们知道，B树删除过程中，如果出现结点的记录数少于半满（即下溢）的情况，则直接把这些记录与其他叶子的记录“融合”，也就是说两个相邻结点合并（因为相邻节点中的点也是顺序的，所以合并相当于线段的延长）。然而R树却是直接重新插入。
具体的例子



这里因为与B树不一样，所以要重新解释一下。因为R11中的c已经被删掉了，所以只剩下了个d。而R树的下溢并不是把d和邻居节点合并了，而是把d要重新插入到整棵R树中，而此时d等同于R11（因为R11中只有一个条目了）。把d放到了待插入列表，说明d已经从树中暂时移除了，就相当于R11没有了。这造成了另一个问题：R4这个条目指向的节点只有R12这一个条目了。这就造成了R12也会下溢，相当于把R12也从R树中临时删掉了，R12要重新插入到R树中。这又造成R4是空节点了，R4会被删除，而R3也会下溢。这就造成了一系列问题。但是关键还是看什么时候执行重插入。

假设结点最大条目数为4，最小条目数为2。在这张图中，我们的目标是删除记录c。首先使用FindLeaf操作找到c所处在的叶子结点的位置——R11。当c从R11删除时，R11就只有一条记录了，少于最小条目数2，出现下溢，此时要调用CondenseTree操作。这样，c被删除，R11剩余的条目——指向记录d的指针——被插入链表Q。然后向更高一层的结点进行此操作。这样R12会被插入链表中，R3及其子树也会插入到链表中。这样整棵树就只剩下了R2这个根节点及其子树，如下图所示。


有一点需要解释的是，我们发现这个删除操作向上传递之后，根结点的条目R1也被插入了Q中，这样根结点只剩下了R2。别着急，重新插入操作会有效的解决这个问题。我们插入R3，R12，d至它原来所处的层。这样，我们发现根结点只有一个条目了，此时根据Inert中的操作，我们把这个根结点删除，它的孩子结点，即R5，R6，R7，R3所在的结点被置为根结点（层数也减少了）。至此，删除操作结束。

另一个例子再次理解删除



所有的叶子节点如上图所示，构成了R树的第一层。



插入节点，构建R树第二层MBB。



构建R树的第三层MBB，如上图所示。最终的树状图如下所示：



准备删除右侧的绿色矩形代表的对象。



直接删除后，绿色的节点里面只有1个entry了，造成下溢，剩下的那个绿色框拿出来放到待插入列表中。同时删掉绿色节点。此时，绿色节点的父节点中的对应entry因为指针为null，也可以删掉了。造成父节点中只有一个entry，它指向的是灰色叶子节点。也就造成了该节点的下溢。



把灰色节点及其子树也放到待插入列表中。



然后把根节点中的中间的那个entry也删掉（根节点剩下2个entry）。



执行重插入操作，把灰色的两级节点作为整体插入到R树中。（我觉得是离黄色、紫色的框近，可能会插入到根节点的左子树中）



（这里只是一个示意，它把灰色框插到了右子树，具体还得看插入算法选的是哪个）。再插入叶子节点，这个一个绿色的叶子，可能会和黄色或者灰色的叶子合并到一个节点中。



第二部分 R树的Java实现

UML



Point

package rtree;/*** @ClassName Point* @Description n维空间中的点，所有的维度被存储在一个float数组中*/
public class Point implements Cloneable {private float[] data;public Point(float[] data) {if (data == null) {throw new IllegalArgumentException("Coordinates cannot be null."); // ★坐标不能为空}if (data.length < 2) {throw new IllegalArgumentException("Point dimension should be greater than 1."); // ★点的维度必须大于1}this.data = new float[data.length];System.arraycopy(data, 0, this.data, 0, data.length); // 复制数组}public Point(int[] data) {if (data == null) {throw new IllegalArgumentException("Coordinates cannot be null."); // ★坐标不能为空}if (data.length < 2) {throw new IllegalArgumentException("Point dimension should be greater than 1."); // ★点的维度必须大于1}this.data = new float[data.length];for (int i = 0; i < data.length; i++) {this.data[i] = data[i]; // 复制数组}}@Override // 重写clone接口protected Object clone() {float[] copy = new float[data.length];System.arraycopy(data, 0, copy, 0, data.length);return new Point(copy);}@Override // 重写tostring（）方法public String toString() {StringBuffer sBuffer = new StringBuffer("(");for (int i = 0; i < data.length - 1; i++) {sBuffer.append(data[i]).append(",");}sBuffer.append(data[data.length - 1]).append(")"); // 最后一位数据后面不再添加逗号，追加放在循环外面return sBuffer.toString();}/** ★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★ ★ 测试 ★* ★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★*/public static void main(String[] args) {float[] test = { 1.2f, 2f, 34f };Point point1 = new Point(test);System.out.println(point1);int[] test2 = { 1, 2, 3, 4 };point1 = new Point(test2);System.out.println(point1);int[] test3 = { 11, 22 }; // 二维的点point1 = new Point(test3);System.out.println(point1);}/*** @return 返回Point的维度*/public int getDimension() {return data.length;}/*** @param index* @return 返回Point坐标第i位的float值*/public float getFloatCoordinate(int index) {return data[index];}/*** @param index* @return 返回Point坐标第i位的int值*/public int getIntCoordinate(int index) {return (int) data[index];}@Overridepublic boolean equals(Object obj) {if (obj instanceof Point) // 如果obj是point的实例{Point point = (Point) obj;if (point.getDimension() != getDimension()) // 维度相同的点才能比较throw new IllegalArgumentException("Points must be of equal dimensions to be compared.");for (int i = 0; i < getDimension(); i++) {if (getFloatCoordinate(i) != point.getFloatCoordinate(i))return false;}}if (!(obj instanceof Point))return false;return true;}
}

Rectangle

package rtree;/*** 外包矩形** @ClassName Rectangle* @Description*/
public class Rectangle implements Cloneable // 继承克隆接口
{private Point low; // 左下角的点private Point high; // 右上角的点public Rectangle(Point p1, Point p2) // 初始化时，第一个参数为左下角，第二个参数为右上角{if (p1 == null || p2 == null) // 点对象不能为空{throw new IllegalArgumentException("Points cannot be null.");}if (p1.getDimension() != p2.getDimension()) // 点的维度应该相等{throw new IllegalArgumentException("Points must be of same dimension.");}// 先左下角后右上角for (int i = 0; i < p1.getDimension(); i++) {if (p1.getFloatCoordinate(i) > p2.getFloatCoordinate(i)) {throw new IllegalArgumentException("坐标点为先左下角后右上角");}}low = (Point) p1.clone();high = (Point) p2.clone();}/*** 返回Rectangle左下角的Point** @return Point*/public Point getLow() {return (Point) low.clone();}/*** 返回Rectangle右上角的Point** @return Point*/public Point getHigh() {return high;}/*** @param rectangle* @return 包围两个Rectangle的最小Rectangle*/public Rectangle getUnionRectangle(Rectangle rectangle) {if (rectangle == null) // 矩形不能为空throw new IllegalArgumentException("Rectangle cannot be null.");if (rectangle.getDimension() != getDimension()) // 矩形维度必须相同{throw new IllegalArgumentException("Rectangle must be of same dimension.");}float[] min = new float[getDimension()];float[] max = new float[getDimension()];for (int i = 0; i < getDimension(); i++) {// 第一个参数是当前矩形的坐标值，第二个参数是传入的参数的矩形的坐标值min[i] = Math.min(low.getFloatCoordinate(i), rectangle.low.getFloatCoordinate(i));max[i] = Math.max(high.getFloatCoordinate(i), rectangle.high.getFloatCoordinate(i));}return new Rectangle(new Point(min), new Point(max));}/*** @return 返回Rectangle的面积*/public float getArea() {float area = 1;for (int i = 0; i < getDimension(); i++) {area *= high.getFloatCoordinate(i) - low.getFloatCoordinate(i);}return area;}/*** @param rectangles* @return 包围一系列Rectangle的最小Rectangle*/public static Rectangle getUnionRectangle(Rectangle[] rectangles) {if (rectangles == null || rectangles.length == 0)throw new IllegalArgumentException("Rectangle array is empty.");Rectangle r0 = (Rectangle) rectangles[0].clone();for (int i = 1; i < rectangles.length; i++) {r0 = r0.getUnionRectangle(rectangles[i]); // 获得包裹矩形r0与r[i]的最小边界的矩形再赋值给r0}return r0; // 返回包围一系列Rectangle的最小Rectangle}@Override// 重写clone()函数protected Object clone() {Point p1 = (Point) low.clone();Point p2 = (Point) high.clone();return new Rectangle(p1, p2);}@Override// 重写tostring()方法public String toString() {return "Rectangle Low:" + low + " High:" + high;}/** ★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★ ★ 测试 ★* ★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★*/public static void main(String[] args) {// 新建两point再根据两个point构建一个Rectanglefloat[] f1 = { 1.3f, 2.4f };float[] f2 = { 3.4f, 4.5f };Point p1 = new Point(f1);Point p2 = new Point(f2);Rectangle rectangle = new Rectangle(p1, p2);System.out.println(rectangle);// Point point = rectangle.getHigh();// point = p1;// System.out.println(rectangle);float[] f_1 = { -2f, 0f };float[] f_2 = { 0f, 2f };float[] f_3 = { -2f, 1f };float[] f_4 = { 3f, 3f };float[] f_5 = { 1f, 0f };float[] f_6 = { 2f, 4f };p1 = new Point(f_1);p2 = new Point(f_2);Point p3 = new Point(f_3);Point p4 = new Point(f_4);Point p5 = new Point(f_5);Point p6 = new Point(f_6);Rectangle re1 = new Rectangle(p1, p2);Rectangle re2 = new Rectangle(p3, p4);Rectangle re3 = new Rectangle(p5, p6);// Rectangle re4 = new Rectangle(p3, p4); //输入要先左下角，再右上角System.out.println(re1.isIntersection(re2));System.out.println(re1.isIntersection(re3));System.out.println(re1.intersectingArea(re2));System.out.println(re1.intersectingArea(re3));}/*** 两个Rectangle相交的面积** @param rectangle*            Rectangle* @return float*/public float intersectingArea(Rectangle rectangle) {if (!isIntersection(rectangle)) // 如果不相交，相交面积为0{return 0;}float ret = 1;// 循环一次，得到一个维度的相交的边，累乘多个维度的相交的边，即为面积for (int i = 0; i < rectangle.getDimension(); i++) {float l1 = this.low.getFloatCoordinate(i);float h1 = this.high.getFloatCoordinate(i);float l2 = rectangle.low.getFloatCoordinate(i);float h2 = rectangle.high.getFloatCoordinate(i);// rectangle1在rectangle2的左边if (l1 <= l2 && h1 <= h2) {ret *= (h1 - l1) - (l2 - l1);}// rectangle1在rectangle2的右边else if (l1 >= l2 && h1 >= h2) {ret *= (h2 - l2) - (l1 - l2);}// rectangle1在rectangle2里面else if (l1 >= l2 && h1 <= h2) {ret *= h1 - l1;}// rectangle1包含rectangle2else if (l1 <= l2 && h1 >= h2) {ret *= h2 - l2;}}return ret;}/*** @param rectangle* @return 判断两个Rectangle是否相交*/public boolean isIntersection(Rectangle rectangle) {if (rectangle == null)throw new IllegalArgumentException("Rectangle cannot be null.");if (rectangle.getDimension() != getDimension()) // 进行判断的两个矩形维度必须相等{throw new IllegalArgumentException("Rectangle cannot be null.");}for (int i = 0; i < getDimension(); i++) {/** 当前矩形左下角的坐标值大于传入矩形右上角的坐标值 || 当前矩形右上角角的坐标值小于传入矩形左下角的坐标值*/if (low.getFloatCoordinate(i) > rectangle.high.getFloatCoordinate(i)|| high.getFloatCoordinate(i) < rectangle.low.getFloatCoordinate(i)) {return false; // 没有相交}}return true;}/*** @return 返回Rectangle的维度*/private int getDimension() {return low.getDimension();}/*** 判断rectangle是否被包围** @param rectangle* @return*/public boolean enclosure(Rectangle rectangle) {if (rectangle == null) // 矩形不能为空throw new IllegalArgumentException("Rectangle cannot be null.");if (rectangle.getDimension() != getDimension()) // 判断的矩形必须维度相同throw new IllegalArgumentException("Rectangle dimension is different from current dimension.");// 只要传入的rectangle有一个维度的坐标越界了就不被包含for (int i = 0; i < getDimension(); i++) {if (rectangle.low.getFloatCoordinate(i) < low.getFloatCoordinate(i)|| rectangle.high.getFloatCoordinate(i) > high.getFloatCoordinate(i))return false;}return true;}@Override// 重写equals方法public boolean equals(Object obj) {if (obj instanceof Rectangle) {Rectangle rectangle = (Rectangle) obj;if (low.equals(rectangle.getLow()) && high.equals(rectangle.getHigh()))return true;}return false;}
}

RTNode

package rtree;import java.util.List;
import rtree.Constants;/*** @ClassName RTNode* @Description*/
public abstract class RTNode {protected RTree rtree; // 结点所在的树protected int level; // 结点所在的层protected Rectangle[] datas; // 相当于条目protected RTNode parent; // 父节点protected int usedSpace; // 结点已用的空间protected int insertIndex; // 记录插入的搜索路径索引protected int deleteIndex; // 记录删除的查找路径索引/*** 构造函数初始化*/public RTNode(RTree rtree, RTNode parent, int level) {this.rtree = rtree;this.parent = parent;this.level = level;datas = new Rectangle[rtree.getNodeCapacity() + 1];// 多出的一个用于结点分裂usedSpace = 0;}/*** @return 返回父节点*/public RTNode getParent() {return parent;}/*** -->向结点中添加Rectangle，即添加条目** @param rectangle*/protected void addData(Rectangle rectangle) {// 如果节点已用空间==r树的节点容量if (usedSpace == rtree.getNodeCapacity()) {throw new IllegalArgumentException("Node is full.");}datas[usedSpace++] = rectangle;}/*** -->删除结点中的第i个条目** @param i*/protected void deleteData(int i) {if (datas[i + 1] != null) // 如果为中间节点（非尾节点），采用拷贝数组的方式链接条目{System.arraycopy(datas, i + 1, datas, i, usedSpace - i - 1);datas[usedSpace - 1] = null;} else // 如果为末尾节点，将节点置空datas[i] = null;// 删除之后已用节点自减usedSpace--;}/*** 压缩算法 叶节点L中刚刚删除了一个条目，如果这个结点的条目数太少下溢， 则删除该结点，同时将该结点中剩余的条目重定位到其他结点中。* 如果有必要，要逐级向上进行这种删除，调整向上传递的路径上的所有外包矩形，使其尽可能小，直到根节点。** @param list*            存储删除结点中剩余条目*/protected void condenseTree(List<RTNode> list) {if (isRoot()) {// 根节点只有一个条目了，即只有左孩子或者右孩子 ，// 将唯一条目删除，释放根节点，将原根节点唯一的孩子设置为新根节点if (!isLeaf() && usedSpace == 1) {RTDirNode root = (RTDirNode) this;RTNode child = root.getChild(0);root.children.remove(this);child.parent = null;rtree.setRoot(child);}} else {RTNode parent = getParent();// 计算节点最小容量，用于判断是否引起下溢int min = Math.round(rtree.getNodeCapacity() * rtree.getFillFactor());if (usedSpace < min) {parent.deleteData(parent.deleteIndex);// 其父节点中删除此条目((RTDirNode) parent).children.remove(this);this.parent = null;list.add(this);// 之前已经把数据删除了} else {parent.datas[parent.deleteIndex] = getNodeRectangle();}parent.condenseTree(list);}}/*** 分裂结点的平方算法* <p>* 1、为两个组选择第一个条目--调用算法pickSeeds()来为两个组选择第一个元素，分别把选中的两个条目分配到两个组当中。<br>* 2、检查是否已经分配完毕，如果一个组中的条目太少，为避免下溢，将剩余的所有条目全部分配到这个组中，算法终止<br>* 3、调用pickNext来选择下一个进行分配的条目--计算把每个条目加入每个组之后面积的增量，选择两个组面积增量差最大的条目索引,* 如果面积增量相等则选择面积较小的组，若面积也相等则选择条目数更少的组<br>** @param rectangle*            导致分裂的溢出Rectangle* @return 两个组中的条目的索引*/protected int[][] quadraticSplit(Rectangle rectangle) {if (rectangle == null) {throw new IllegalArgumentException("Rectangle cannot be null.");}datas[usedSpace] = rectangle; // 先添加进去int total = usedSpace + 1; // 结点总数// 标记访问的条目int[] mask = new int[total];for (int i = 0; i < total; i++) {mask[i] = 1;}// 分裂后每个组只是有total/2个条目int c = total / 2 + 1;// 每个结点最小条目个数int minNodeSize = Math.round(rtree.getNodeCapacity() * rtree.getFillFactor());// 至少有两个if (minNodeSize < 2)minNodeSize = 2;// 记录没有被检查的条目的个数int rem = total;int[] group1 = new int[c];// 记录分配的条目的索引int[] group2 = new int[c];// 记录分配的条目的索引// 跟踪被插入每个组的条目的索引int i1 = 0, i2 = 0;int[] seed = pickSeeds();group1[i1++] = seed[0];group2[i2++] = seed[1];rem -= 2;mask[group1[0]] = -1;mask[group2[0]] = -1;while (rem > 0) {// 将剩余的所有条目全部分配到group1组中，算法终止if (minNodeSize - i1 == rem) {for (int i = 0; i < total; i++)// 总共rem个{if (mask[i] != -1)// 还没有被分配{group1[i1++] = i;mask[i] = -1;rem--;}}// 将剩余的所有条目全部分配到group1组中，算法终止} else if (minNodeSize - i2 == rem) {for (int i = 0; i < total; i++)// 总共rem个{if (mask[i] != -1)// 还没有被分配{group2[i2++] = i;mask[i] = -1;rem--;}}} else {// 求group1中所有条目的最小外包矩形Rectangle mbr1 = (Rectangle) datas[group1[0]].clone();for (int i = 1; i < i1; i++) {mbr1 = mbr1.getUnionRectangle(datas[group1[i]]);}// 求group2中所有条目的外包矩形Rectangle mbr2 = (Rectangle) datas[group2[0]].clone();for (int i = 1; i < i2; i++) {mbr2 = mbr2.getUnionRectangle(datas[group2[i]]);}// 找出下一个进行分配的条目double dif = Double.NEGATIVE_INFINITY;double areaDiff1 = 0, areaDiff2 = 0;int sel = -1;for (int i = 0; i < total; i++) {if (mask[i] != -1)// 还没有被分配的条目{// 计算把每个条目加入每个组之后面积的增量，选择两个组面积增量差最大的条目索引Rectangle a = mbr1.getUnionRectangle(datas[i]);areaDiff1 = a.getArea() - mbr1.getArea();Rectangle b = mbr2.getUnionRectangle(datas[i]);areaDiff2 = b.getArea() - mbr2.getArea();if (Math.abs(areaDiff1 - areaDiff2) > dif) {dif = Math.abs(areaDiff1 - areaDiff2);sel = i;}}}if (areaDiff1 < areaDiff2)// 先比较面积增量{group1[i1++] = sel;} else if (areaDiff1 > areaDiff2) {group2[i2++] = sel;} else if (mbr1.getArea() < mbr2.getArea())// 再比较自身面积{group1[i1++] = sel;} else if (mbr1.getArea() > mbr2.getArea()) {group2[i2++] = sel;} else if (i1 < i2)// 最后比较条目个数{group1[i1++] = sel;} else if (i1 > i2) {group2[i2++] = sel;} else {group1[i1++] = sel;}mask[sel] = -1;rem--;}} // end whileint[][] ret = new int[2][];ret[0] = new int[i1];ret[1] = new int[i2];for (int i = 0; i < i1; i++) {ret[0][i] = group1[i];}for (int i = 0; i < i2; i++) {ret[1][i] = group2[i];}return ret;}/*** 1、对每一对条目E1和E2，计算包围它们的Rectangle J，计算d = area(J) - area(E1) - area(E2);<br>* 2、Choose the pair with the largest d** @return 返回两个条目如果放在一起会有最多的冗余空间的条目索引*/protected int[] pickSeeds() {double inefficiency = Double.NEGATIVE_INFINITY;int i1 = 0, i2 = 0;// 两个for循环对任意两个条目E1和E2进行组合for (int i = 0; i < usedSpace; i++) {for (int j = i + 1; j <= usedSpace; j++)// 注意此处的j值{Rectangle rectangle = datas[i].getUnionRectangle(datas[j]);double d = rectangle.getArea() - datas[i].getArea() - datas[j].getArea();if (d > inefficiency) {inefficiency = d;i1 = i;i2 = j;}}}return new int[] { i1, i2 }; // 返回拥有最小d的一对条目}/*** @return 返回包含结点中所有条目的最小Rectangle*/public Rectangle getNodeRectangle() {if (usedSpace > 0) {Rectangle[] rectangles = new Rectangle[usedSpace];System.arraycopy(datas, 0, rectangles, 0, usedSpace);return Rectangle.getUnionRectangle(rectangles); // 返回包含这一系列矩形的最小矩形} else {return new Rectangle(new Point(new float[] { 0, 0 }), new Point(new float[] { 0, 0 }));}}/*** @return 是否根节点*/public boolean isRoot() {return (parent == Constants.NULL);}/*** @return 是否非叶子结点*/public boolean isIndex() {return (level != 0);}/*** @return 是否叶子结点*/public boolean isLeaf() {return (level == 0);}/*** <b>步骤CL1：</b>初始化――记R树的根节点为N。<br>* <b>步骤CL2：</b>检查叶节点――如果N是个叶节点，返回N<br>* <b>步骤CL3：</b>选择子树――如果N不是叶节点，则从N中所有的条目中选出一个最佳的条目F，* 选择的标准是：如果E加入F后，F的外廓矩形FI扩张最小，则F就是最佳的条目。如果有两个* 条目在加入E后外廓矩形的扩张程度相等，则在这两者中选择外廓矩形较小的那个。<br>* <b>步骤CL4：</b>向下寻找直至达到叶节点――记Fp指向的孩子节点为N，然后返回步骤CL2循环运算， 直至查找到叶节点。* <p>** @param Rectangle* @return RTDataNode*/protected abstract RTDataNode chooseLeaf(Rectangle rectangle);/*** R树的根节点为T，查找包含rectangle的叶子结点* <p>* 1、如果T不是叶子结点，则逐个查找T中的每个条目是否包围rectangle，若包围则递归调用findLeaf()<br>* 2、如果T是一个叶子结点，则逐个检查T中的每个条目能否匹配rectangle<br>** @param rectangle* @return 返回包含rectangle的叶节点*/protected abstract RTDataNode findLeaf(Rectangle rectangle);}

RTDataNode

package rtree;import java.util.ArrayList;
import java.util.List;import rtree.Constants;/*** @ClassName RTDataNode* @Description 叶子结点*/
public class RTDataNode extends RTNode {public RTDataNode(RTree rTree, RTNode parent) {super(rTree, parent, 0);}/*** -->叶节点中插入Rectangle 在叶节点中插入Rectangle，插入后如果其父节点不为空则需要向上调整树直到根节点；* 如果其父节点为空，则是从根节点插入 若插入Rectangle之后超过结点容量则需要分裂结点 【注】插入数据后，从parent处开始调整数据** @param rectangle* @return*/public boolean insert(Rectangle rectangle) {if (usedSpace < rtree.getNodeCapacity()) // 已用节点小于节点容量{datas[usedSpace++] = rectangle;RTDirNode parent = (RTDirNode) getParent();if (parent != null)// 调整树，但不需要分裂节点，因为 节点小于节点容量，还有空间parent.adjustTree(this, null);return true;}// 超过结点容量else {RTDataNode[] splitNodes = splitLeaf(rectangle);RTDataNode l = splitNodes[0];RTDataNode ll = splitNodes[1];if (isRoot()) {// 根节点已满，需要分裂。创建新的根节点RTDirNode rDirNode = new RTDirNode(rtree, Constants.NULL, level + 1);rtree.setRoot(rDirNode);// getNodeRectangle()返回包含结点中所有条目的最小RectanglerDirNode.addData(l.getNodeRectangle());rDirNode.addData(ll.getNodeRectangle());ll.parent = rDirNode;l.parent = rDirNode;rDirNode.children.add(l);rDirNode.children.add(ll);} else {// 不是根节点RTDirNode parentNode = (RTDirNode) getParent();parentNode.adjustTree(l, ll);}}return true;}/*** 叶子节点的分裂 插入Rectangle之后超过容量需要分裂** @param rectangle* @return*/public RTDataNode[] splitLeaf(Rectangle rectangle) {int[][] group = null;switch (rtree.getTreeType()) {case Constants.RTREE_LINEAR:break;case Constants.RTREE_QUADRATIC:group = quadraticSplit(rectangle);break;case Constants.RTREE_EXPONENTIAL:break;case Constants.RSTAR:break;default:throw new IllegalArgumentException("Invalid tree type.");}RTDataNode l = new RTDataNode(rtree, parent);RTDataNode ll = new RTDataNode(rtree, parent);int[] group1 = group[0];int[] group2 = group[1];for (int i = 0; i < group1.length; i++) {l.addData(datas[group1[i]]);}for (int i = 0; i < group2.length; i++) {ll.addData(datas[group2[i]]);}return new RTDataNode[] { l, ll };}@Overridepublic RTDataNode chooseLeaf(Rectangle rectangle) {insertIndex = usedSpace;// 记录插入路径的索引return this;}/*** 从叶节点中删除此条目rectangle* <p>* 先删除此rectangle，再调用condenseTree()返回删除结点的集合，把其中的叶子结点中的每个条目重新插入；* 非叶子结点就从此结点开始遍历所有结点，然后把所有的叶子结点中的所有条目全部重新插入** @param rectangle* @return*/protected int delete(Rectangle rectangle) {for (int i = 0; i < usedSpace; i++) {if (datas[i].equals(rectangle)) {deleteData(i);// 用于存储被删除的结点包含的条目的链表QList<RTNode> deleteEntriesList = new ArrayList<RTNode>();condenseTree(deleteEntriesList);// 重新插入删除结点中剩余的条目for (int j = 0; j < deleteEntriesList.size(); j++) {RTNode node = deleteEntriesList.get(j);if (node.isLeaf())// 叶子结点，直接把其上的数据重新插入{for (int k = 0; k < node.usedSpace; k++) {rtree.insert(node.datas[k]);}} else {// 非叶子结点，需要先后序遍历出其上的所有结点List<RTNode> traverseNodes = rtree.traversePostOrder(node);// 把其中的叶子结点中的条目重新插入for (int index = 0; index < traverseNodes.size(); index++) {RTNode traverseNode = traverseNodes.get(index);if (traverseNode.isLeaf()) {for (int t = 0; t < traverseNode.usedSpace; t++) {rtree.insert(traverseNode.datas[t]);}}}}}return deleteIndex;} // end if} // end forreturn -1;}@Overrideprotected RTDataNode findLeaf(Rectangle rectangle) {for (int i = 0; i < usedSpace; i++) {if (datas[i].enclosure(rectangle)) {deleteIndex = i;// 记录搜索路径return this;}}return null;}}

RTDirNode

package rtree;import java.util.ArrayList;
import java.util.List;
import rtree.Constants;/*** @ClassName RTDirNode* @Description 非叶节点*/
public class RTDirNode extends RTNode {/*** 孩子结点集*/protected List<RTNode> children;// 构造函数public RTDirNode(RTree rtree, RTNode parent, int level) {super(rtree, parent, level); // 调用父类的构造函数children = new ArrayList<RTNode>(); // 新建一个RTNode类型的结点数组}/*** @param index* @return 对应索引下的孩子结点*/public RTNode getChild(int index) {return children.get(index);}@Override/*-->选择叶子结点*/public RTDataNode chooseLeaf(Rectangle rectangle) {int index;switch (rtree.getTreeType()) {case Constants.RTREE_LINEAR:case Constants.RTREE_QUADRATIC:case Constants.RTREE_EXPONENTIAL:index = findLeastEnlargement(rectangle); // 获得面积增量最小的结点的索引break;case Constants.RSTAR:if (level == 1)// 即此结点指向叶节点{index = findLeastOverlap(rectangle); // 获得最小重叠面积的结点的索引} else {index = findLeastEnlargement(rectangle); // 获得面积增量最小的结点的索引}break;default:throw new IllegalStateException("Invalid tree type.");}insertIndex = index;// 记录插入路径的索引return getChild(index).chooseLeaf(rectangle); // 非叶子节点的chooseLeaf（）实现递归调用}/*** @param rectangle* @return -->返回最小重叠面积的结点的索引， 如果重叠面积相等则选择加入此Rectangle后面积增量更小的，*         如果面积增量还相等则选择自身面积更小的*/private int findLeastOverlap(Rectangle rectangle) {float overlap = Float.POSITIVE_INFINITY;int sel = -1;for (int i = 0; i < usedSpace; i++) {RTNode node = getChild(i);float ol = 0; // 用于记录每个孩子的datas数据与传入矩形的重叠面积之和for (int j = 0; j < node.datas.length; j++) {// 将传入矩形与各个矩形重叠的面积累加到ol中，得到重叠的总面积ol += rectangle.intersectingArea(node.datas[j]);}if (ol < overlap) {overlap = ol;// 记录重叠面积最小的sel = i;// 记录第几个孩子的索引}// 如果重叠面积相等则选择加入此Rectangle后面积增量更小的,如果面积增量还相等则选择自身面积更小的else if (ol == overlap) {double area1 = datas[i].getUnionRectangle(rectangle).getArea() - datas[i].getArea();double area2 = datas[sel].getUnionRectangle(rectangle).getArea() - datas[sel].getArea();if (area1 == area2) {sel = (datas[sel].getArea() <= datas[i].getArea()) ? sel : i;} else {sel = (area1 < area2) ? i : sel;}}}return sel;}/*** @param rectangle* @return -->面积增量最小的结点的索引，如果面积增量相等则选择自身面积更小的*/private int findLeastEnlargement(Rectangle rectangle) {double area = Double.POSITIVE_INFINITY; // double类型的正无穷int sel = -1;for (int i = 0; i < usedSpace; i++) {// 增量enlargement = 包含（datas[i]里面存储的矩形与查找的矩形）的最小矩形的面积 -// datas[i]里面存储的矩形的面积double enlargement = datas[i].getUnionRectangle(rectangle).getArea() - datas[i].getArea();if (enlargement < area) {area = enlargement; // 记录增量sel = i; // 记录引起增量的【包含（datas[i]里面存储的矩形与查找的矩形）的最小矩形】里面的datas[i]的索引} else if (enlargement == area) {sel = (datas[sel].getArea() < datas[i].getArea()) ? sel : i;}}return sel;}/*** --> 插入新的Rectangle后从插入的叶节点开始向上调整RTree，直到根节点** @param node1*            引起需要调整的孩子结点* @param node2*            分裂的结点，若未分裂则为null*/public void adjustTree(RTNode node1, RTNode node2) {// 先要找到指向原来旧的结点（即未添加Rectangle之前）的条目的索引datas[insertIndex] = node1.getNodeRectangle();// 先用node1覆盖原来的结点children.set(insertIndex, node1);// 替换旧的结点if (node2 != null) {insert(node2);// 插入新的结点}// 还没到达根节点else if (!isRoot()) {RTDirNode parent = (RTDirNode) getParent();parent.adjustTree(this, null);// 向上调整直到根节点}}/*** -->非叶子节点插入** @param node* @return 如果结点需要分裂则返回true*/protected boolean insert(RTNode node) {// 已用结点小于树的节点容量，不需分裂，只需插入以及调整树if (usedSpace < rtree.getNodeCapacity()) {datas[usedSpace++] = node.getNodeRectangle();children.add(node);// 新加的node.parent = this;// 新加的RTDirNode parent = (RTDirNode) getParent();if (parent != null) // 不是根节点{parent.adjustTree(this, null);}return false;} else {// 非叶子结点需要分裂RTDirNode[] a = splitIndex(node);RTDirNode n = a[0];RTDirNode nn = a[1];if (isRoot()) {// 新建根节点，层数加1RTDirNode newRoot = new RTDirNode(rtree, Constants.NULL, level + 1);// 把两个分裂的结点n和nn添加到根节点newRoot.addData(n.getNodeRectangle());newRoot.addData(nn.getNodeRectangle());newRoot.children.add(n);newRoot.children.add(nn);// 设置两个分裂的结点n和nn的父节点n.parent = newRoot;nn.parent = newRoot;// 最后设置rtree的根节点rtree.setRoot(newRoot);// 新加的} else {// 如果不是根结点，向上调整树RTDirNode p = (RTDirNode) getParent();p.adjustTree(n, nn);}}return true;}/*** -->非叶子结点的分裂** @param node* @return*/private RTDirNode[] splitIndex(RTNode node) {int[][] group = null;switch (rtree.getTreeType()) {case Constants.RTREE_LINEAR:break;case Constants.RTREE_QUADRATIC:group = quadraticSplit(node.getNodeRectangle());children.add(node);// 新加的node.parent = this;// 新加的break;case Constants.RTREE_EXPONENTIAL:break;case Constants.RSTAR:break;default:throw new IllegalStateException("Invalid tree type.");}// 新建两个非叶子节点RTDirNode index1 = new RTDirNode(rtree, parent, level);RTDirNode index2 = new RTDirNode(rtree, parent, level);int[] group1 = group[0];int[] group2 = group[1];// 为index1添加数据和孩子for (int i = 0; i < group1.length; i++) {index1.addData(datas[group1[i]]);index1.children.add(this.children.get(group1[i]));// 新加的// 让index1成为其父节点this.children.get(group1[i]).parent = index1;// 新加的}for (int i = 0; i < group2.length; i++) {index2.addData(datas[group2[i]]);index2.children.add(this.children.get(group2[i]));// 新加的this.children.get(group2[i]).parent = index2;// 新加的}return new RTDirNode[] { index1, index2 };}@Override// 寻找叶子protected RTDataNode findLeaf(Rectangle rectangle) {for (int i = 0; i < usedSpace; i++) {if (datas[i].enclosure(rectangle)) {deleteIndex = i;// 记录搜索路径RTDataNode leaf = children.get(i).findLeaf(rectangle); // 递归查找if (leaf != null)return leaf;}}return null;}}

Rtree

package rtree;import java.util.ArrayList;
import java.util.List;import rtree.Constants;/*** @ClassName RTree* @Description*/
public class RTree {private RTNode root; // 根节点private int tree_type; // 树类型private int nodeCapacity = -1; // 结点容量private float fillFactor = -1; // 结点填充因子 ，用于计算每个结点最小条目个数private int dimension; // 维度public RTree(int capacity, float fillFactor, int type, int dimension) {this.fillFactor = fillFactor;tree_type = type;nodeCapacity = capacity;this.dimension = dimension;root = new RTDataNode(this, Constants.NULL); // 根节点的父节点为NULL}/*** @return RTree的维度*/public int getDimension() {return dimension;}/** 设置跟节点 */public void setRoot(RTNode root) {this.root = root;}/*** @return 填充因子*/public float getFillFactor() {return fillFactor;}/*** @return 返回结点容量*/public int getNodeCapacity() {return nodeCapacity;}/*** @return 返回树的类型*/public int getTreeType() {return tree_type;}/*** --> 向Rtree中插入Rectangle 1、先找到合适的叶节点 2、再向此叶节点中插入** @param rectangle*/public boolean insert(Rectangle rectangle) {if (rectangle == null)throw new IllegalArgumentException("Rectangle cannot be null.");if (rectangle.getHigh().getDimension() != getDimension()) // 矩形维度与树的维度不一致{throw new IllegalArgumentException("Rectangle dimension different than RTree dimension.");}RTDataNode leaf = root.chooseLeaf(rectangle);return leaf.insert(rectangle);}/*** 从R树中删除Rectangle* <p>* 1、寻找包含记录的结点--调用算法findLeaf()来定位包含此记录的叶子结点L，如果没有找到则算法终止。<br>* 2、删除记录--将找到的叶子结点L中的此记录删除<br>* 3、调用算法condenseTree<br>** @param rectangle* @return*/public int delete(Rectangle rectangle) {if (rectangle == null) {throw new IllegalArgumentException("Rectangle cannot be null.");}if (rectangle.getHigh().getDimension() != getDimension()) {throw new IllegalArgumentException("Rectangle dimension different than RTree dimension.");}RTDataNode leaf = root.findLeaf(rectangle);if (leaf != null) {return leaf.delete(rectangle);}return -1;}/*** 从给定的结点root开始遍历所有的结点** @param node* @return 所有遍历的结点集合*/public List<RTNode> traversePostOrder(RTNode root) {if (root == null)throw new IllegalArgumentException("Node cannot be null.");List<RTNode> list = new ArrayList<RTNode>();list.add(root);if (!root.isLeaf()) {for (int i = 0; i < root.usedSpace; i++) {List<RTNode> a = traversePostOrder(((RTDirNode) root).getChild(i));for (int j = 0; j < a.size(); j++) {list.add(a.get(j));}}}return list;}public static void main(String[] args) throws Exception {// 结点容量：4、填充因子：0.4、树类型：二维RTree tree = new RTree(4, 0.4f, Constants.RTREE_QUADRATIC, 2);// 每一行的四个数构成两个点（一个矩形）float[] f = { 5, 30, 25, 35, 15, 38, 23, 50, 10, 23, 30, 28, 13, 10, 18, 15, 23, 10, 28, 20, 28, 30, 33, 40, 38,13, 43, 30, 35, 37, 40, 43, 45, 8, 50, 50, 23, 55, 28, 70, 10, 65, 15, 70, 10, 58, 20, 63, };// 插入结点for (int i = 0; i < f.length;) {Point p1 = new Point(new float[] { f[i++], f[i++] });Point p2 = new Point(new float[] { f[i++], f[i++] });final Rectangle rectangle = new Rectangle(p1, p2);tree.insert(rectangle);Rectangle[] rectangles = tree.root.datas;System.out.println("level:" + tree.root.level);for (int j = 0; j < rectangles.length; j++)System.out.println(rectangles[j]);}System.out.println("---------------------------------");System.out.println("Insert finished.");// 删除结点System.out.println("---------------------------------");System.out.println("Begin delete.");for (int i = 0; i < f.length;) {Point p1 = new Point(new float[] { f[i++], f[i++] });Point p2 = new Point(new float[] { f[i++], f[i++] });final Rectangle rectangle = new Rectangle(p1, p2);tree.delete(rectangle);Rectangle[] rectangles = tree.root.datas;System.out.println(tree.root.level);for (int j = 0; j < rectangles.length; j++)System.out.println(rectangles[j]);}System.out.println("---------------------------------");System.out.println("Delete finished.");Rectangle[] rectangles = tree.root.datas;for (int i = 0; i < rectangles.length; i++)System.out.println(rectangles[i]);}}

Constants

package rtree;import rtree.RTNode;public class Constants {public static final int MAX_NUMBER_OF_ENTRIES_IN_NODE = 20;// 结点中的最大条目数public static final int MIN_NUMBER_OF_ENTRIES_IN_NODE = 8;// 结点中的最小条目数public static final int RTDataNode_Dimension = 2;/** Available RTree variants. */ // 树的类型常量public static final int RTREE_LINEAR = 0; // 线性public static final int RTREE_QUADRATIC = 1; // 二维public static final int RTREE_EXPONENTIAL = 2; // 多维public static final int RSTAR = 3; // 星型public static final int NIL = -1;public static final RTNode NULL = null;
}

参考文章：
1.从B树、B+树、B*树谈到R 树 http://blog.csdn.net/v_JULY_v/article/details/6530142/

2.R树的Java实现 http://blog.csdn.net/renyisheng/article/details/40347223

3.R树wiki https://en.wikipedia.org/wiki/R-tree