本文主要是介绍单因素方差分析--R,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
任务说明
三个剂量水平的药物处理受试者,每个剂量水平十个受试者,现在收集到数据后,问:
药物剂量水平显著影响受试者的response?
或者不同剂量药物处理受试者有显著效果的差异吗?
数据
library(tidyverse)
library(reshape2)
# install.packages("gplots")
library(gplots)
df <- read.table("AUClast1.csv",header = T,sep=",")
head(df)
dose <- c(0.2,0.6,1.8)
fqr <- as.data.frame(t(df[1:3,2:11]))
rownames(fqr) <- 1:nrow(fqr)
colnames(fqr) <- dose
fqr <- melt(fqr)
fqr$variable <- as.factor(fqr$variable)
head(fqr)
# variable value
#1 0.2 24.9
#2 0.2 19.7
#3 0.2 27.3
#4 0.2 26.8
#5 0.2 30.8
#6 0.2 30.2table(fqr$variable)
# 0.2 0.6 1.8
# 10 10 10
代码
# anove单因素方差分析
fit <- aov(value ~ variable,fqr)
summary(fit)
# Df Sum Sq Mean Sq F value Pr(>F)
# variable 2 593525 296762 45.6 2.2e-09
# Residuals 27 175587 6503
# 分组之间的均值差异显著# 可视化
plotmeans(fqr$value ~ fqr$variable, xlab="Treatment", ylab="Response",main="Mean Plot\nwith 95% CI")# 1.8的剂量分组 内部方差太大了,不过还是继续看看,后面做一下假设检验证实一下。
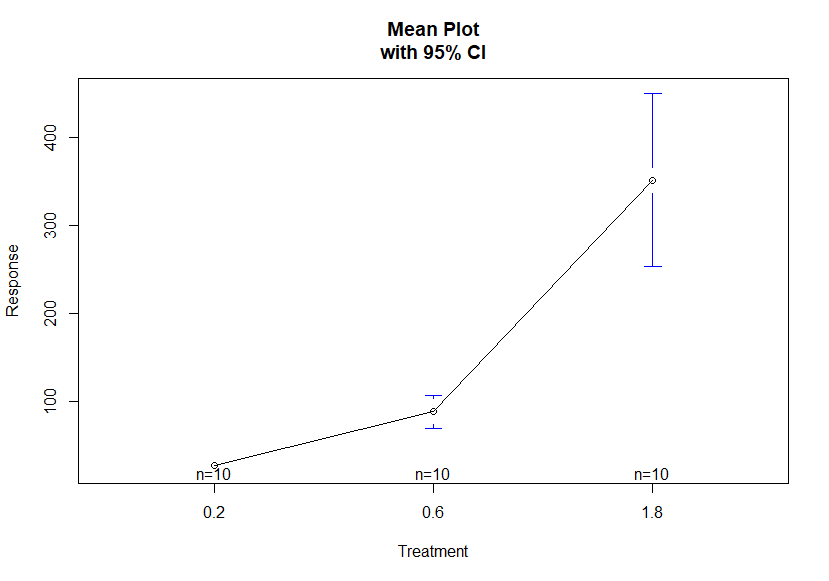
# 上述分析只知道组件均值差异大但是不知那几组之间差异大,需要多重比较才能知晓(杜肯法,最小极差法等等)
# 多重比较
library(multcomp)# par语句扩大了图像的顶部面积
par(mar=c(5,4,6,2))
# 进行多重比较
tuk <- glht(fit, linfct=mcp(variable="Tukey"))
# 图像展示
# 有相同字母的两组即为不显著差异
plot(cld(tuk, level=.05),col="lightgrey")# 0.2剂量组和0.6剂量组的response均值无明显差异,图像顶部都是a
# 1.8剂量组和0.2剂量组或0.6剂量组的response均值相比较均有明显差异,图像顶部的字母不一致
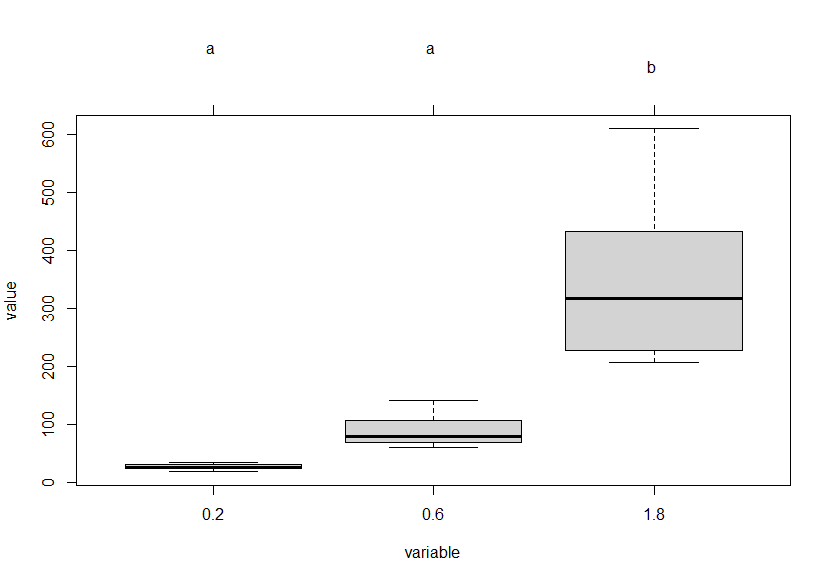
# 上面的boxplot可以明显看到1.8剂量组的组内方差很大的,到底是组内方差还是组间方差引起了显著性差异呢?
# 做一下 ”评估方差检验的假设条件“
# 1. 因变量的正态分布
library(car)qqPlot(lm(value ~ variable, data=fqr),simulate=TRUE, main="Q-Q Plot", labels=FALSE)
# 不满足
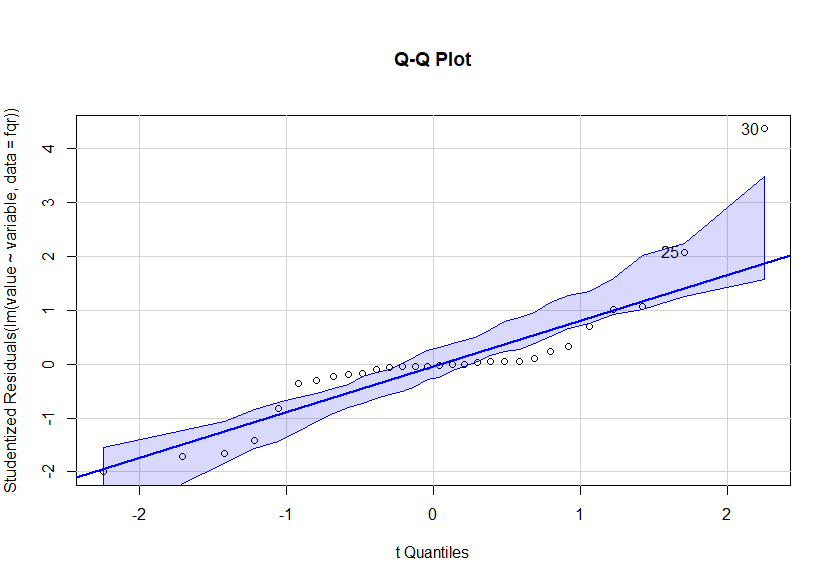
# 2.离群点检测
library(car)outlierTest(fit)# rstudent unadjusted p-value Bonferroni p
# 30 4.367 0.0001784 0.005352
# 第三十个数据点是离群点(去掉离群点后拟合还有可能出现离群点)
# 3. 因变量的方差齐性
bartlett.test(value ~ variable, data=fqr)
# Bartlett检验表明三组的方差有明显的不同(p-value = 1e-13)
结论
# 数据包含强影响点,而且因变量(误差)不满足正态分布
# 方差齐性分析也证实了 分组之间的组内放差有明显的不同
# 组内方差较大时,实验的结果无法解释,所以整个方差分析的结果也不可信。
这篇关于单因素方差分析--R的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






