LeetCode 501. 二叉搜索树中的众数(Java版暴打官方，还有谁(前序遍历+Mirrot+两次遍历真正的O(1)))

本文主要是介绍LeetCode 501. 二叉搜索树中的众数(Java版暴打官方，还有谁(前序遍历+Mirrot+两次遍历真正的O(1)))，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言

给你一个含重复值的二叉搜索树（BST）的根节点 root ，找出并返回 BST 中的所有众数（即，出现频率最高的元素）。
假定 BST 满足如下定义：

结点左子树中所含节点的值小于等于当前节点的值
结点右子树中所含节点的值大于等于当前节点的值
左子树和右子树都是二叉搜索树

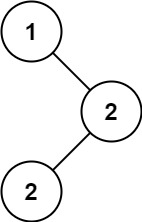
输入：root = [1,null,2,2]
输出：[2]
如果树中有不止一个众数，可以按任意顺序返回。

第一种解法：前序遍历

利用二叉搜索树的性质，中序遍历一定是有序的，也就是相同的数一定会挨在一起；

我们可以用一个base来表示前一个数的值，max表示最多的数(也就是众数)的个数；

每次当前节点与前一个节点相同时，我们就把number+1，否则则更新base，number的值
然后再判断number是否与max相同，相同的话，则将该数添加到list结果数组中，表示该数也是一个众数；
如果number>max的话，则清空list结果数组，表示该数目前是唯一一个众数

那么如何记录前一个节点呢，我们利用中序遍历便可以记录下前一个节点，因为中序遍历是有序的。

class Solution {//保存前一个数的值int base=Integer.MIN_VALUE;//保存当前众数的个数int max=0;//保存当前这个值的个数int number=0;public int[] findMode(TreeNode root) {List<Integer> list=new ArrayList<>();dfs(root,list);//将list转换为int数组return list.stream().mapToInt(Integer::intValue).toArray();}//这里采用中序遍历，这样的话base每次就是它的前一个节点private void dfs(TreeNode root, List<Integer> list) {if (root==null) return;dfs(root.left,list);if(root.val==base){//如果当前节点的这个数等于前一个节点的数，则number数量+1number++;}else{//如果当前节点的这个数不等于前一个节点数，则更新base为当前节点值，number为1base=root.val;number=1;}if(max==number){//如果当前节点的数量等于当前众数的个数，则添加这个节点list.add(root.val);}else if(number>max){//如果当前节点的数量大于当前众数的个数，则清空众数数组，并更新众数数组为当前节点值max=number;list.clear();list.add(root.val);}dfs(root.right,list);}
}

时间复杂度为O(n),空间复杂度为O(1)
list为临时数组，与个数无关；且栈空间不计

第二种解法：Mirror算法

不清楚Mirror算法的可以去图解Mirror算法这里先看明白

class Solution {List<Integer> list=new ArrayList<>();//保存前一个数int base;//保存前一个数的个数int preNumber;//保存当前众数的个数int maxNumber;//Mirror算法public int[] findMode(TreeNode root) {while(root!=null){if(root.left!=null){TreeNode cur=root.left;while(cur.right!=null&&cur.right!=root){cur=cur.right;}if(cur.right==null){cur.right=root;root=root.left;}if(cur.right==root){updata(root.val);cur.right=null;root=root.right;}}else{updata(root.val);root=root.right;}}return list.stream().mapToInt(Integer::intValue).toArray();}private void updata(int val) {if(val==base)preNumber++;else{base=val;preNumber=1;}if(preNumber==maxNumber)list.add(base);else if(preNumber>maxNumber){maxNumber=preNumber;list.clear();list.add(val);}}
}

时间复杂度为O(n),空间复杂度为O(1),比上一个解法少了栈空间

第三种解法：两次遍历

这种解法空间复杂度达到了真正的O(1)，但是两次遍历，也就是所谓的时间换空间

其实三种方法都是一个思想，因为是二叉搜索树，所以都是利用了保存前一个节点来进行的各种操作，只不过保存前一个节点的方式不一样而已

class Solution {//保存前一个数int base;//保存前一个数的个数int preNumber;//保存当前众数的个数int maxNumber;//结果数组int[] res;//结果数组的个数int resNum=0;//当前结果数组的个数int i=0;//两次遍历算法public int[] findMode(TreeNode root) {mirror(root);base=Integer.MIN_VALUE;preNumber=0;res=new int[resNum];mirror(root);return res;}private void mirror(TreeNode root){while(root!=null){if(root.left!=null){TreeNode cur=root.left;while(cur.right!=null&&cur.right!=root){cur=cur.right;}if(cur.right==null){cur.right=root;root=root.left;}if(cur.right==root){updata(root.val);cur.right=null;root=root.right;}}else{updata(root.val);root=root.right;}}}private void updata(int val) {if(val==base)preNumber++;else{base=val;preNumber=1;}if(preNumber==maxNumber){resNum++;if(res!=null) {res[i]=val;i++;}}else if(preNumber>maxNumber){resNum=1;maxNumber=preNumber;}}
}