C++ 遗传学SFLA混合蛙跳算法

本文主要是介绍C++ 遗传学SFLA混合蛙跳算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

蛙跳算法（Shuffled Frog Leading Algorithm）是一种启发式算法，通过启发式函数进行启发式搜索，从而找到组合最优问题的解。

他结合了以遗传为基础的memetic算法和以社会行为为基础的粒子群优化算法的优点。也可以说SFLA=SCE+PSO

一、问题概念：

蛙跳算法的思想是：在一片湿地中生活着一群青蛙。湿地内离散的分布着许多石头，青蛙通过寻找不同的石头进行跳跃去找到食物较多的地方。每只青蛙个体之间通过文化的交流实现信息的交换。每只青蛙都具有自己的文化。每只青蛙的文化被定义为问题的一个解。湿地的整个青蛙群体被分为不同的子群体，每个子群体有着自己的文化，执行局部搜索策略。在子群体中的每个个体有着自己的文化，并且影响着其他个体，也受其他个体的影响，并随着子群体的进化而进化。当子群体进化到一定阶段以后，各个子群体之间再进行思想的交流（全局信息交换）实现子群体间的混合运算，一直到所设置的条件满足为止。

二、解决思路：

在SFLA中，种群被分为若干个子群（memeplex），每一个子群包括一定数量的青蛙。不同的memeplex具有不同的文化，分别进行局部搜索。在每个子群中，每只青蛙都有自己的想法，并且受到其他青蛙想法的影响，通过memetic进化来发展。这样经过一定的memetic进化以及跳跃过程，这些想法思路就在各个memeplex中传播开来，然后，据需局部搜索和跳跃，知道收敛或满足标准为止。

可以这样理解，所有的个体（青蛙）都在朝向相对更优的解进化，然后经过给定的周期（设置的迭代次数）后，再看其所有个体的进化程度。算法的思想是每个个体所含在的基因都朝向一个目标发展（子群最优、全局最优），就像我们会向更优秀的人索取经验、期望和更优秀的人保持更多的相同点一个道理。

三、基本参数

蛙群的数量；
族群的数量；
族群中青蛙的数量；
最大允许跳动步长；
全局最好解；
局部最好解；
局部最差解；
子族群中青蛙的数量；
局部元进化次数；
全局思想交流次数等。

四、算法实现

4.1 初始化

定义基本参数

#define G 100  /*混合迭代次数*/
#define M 3 /*族群数*/
#define I 5 /*一个族群中的个体数*/
#define P M*I /*个体总数*/
#define V 20 /*个体基因维数*/
#define N 10 /*族群内更新次数*/
#define MAX 1000.0/*随机最大值*/
#define MIN -1000.0/*随机最小值*/
#define D 2.0 /*蛙跳的最大值*/
#define R (rand()%100)/100.0
typedef struct {double d[V];double value;
}Individal;
Individal pw[M];/*族群中个体最差*/
Individal pb[M];/*族群中个体最好*/
Individal pg;/*全体中最好*/
Individal group[P];/*整体*/
Individal memeplex[M][I];/*族群*/

生成蛙群，每只蛙个体包括基因维数数组以及价值（适应度）

double fitness(Individal individal)
{int i;double sum = 0;for (i = 0; i<V - 1; i++){sum += pow(individal.d[0] - 0, 2);}return sum;
}void init()
{int i, j;for (i = 0; i<P; i++){for (j = 0; j<V; j++){group[i].d[j] = R*(MAX - MIN) + MIN;}group[i].value = fitness(group[i]);}
}

注：为了观察进化效率，这里我们暂时用差值平方代表适应度

4.2个体排序分组

对青蛙划分等级。将青蛙按照性能的好坏依次排列，生成数组：记录最好青蛙pg，同时对其进行分组（将数组group分成为m个memeplex）

void sort()
{int i, j, k;qsort(group, P, sizeof(Individal), mycmp);k = 0;/*分组*/for (i = 0; i<I; i++){for (j = 0; j<M; j++){memeplex[j][i] = group[k];k++;}}pg = group[P - 1];for (i = 0; i<M; i++){pw[i] = memeplex[i][0];pb[i] = memeplex[i][I - 1];}
}

4.3组内进化（memetic）

4.3.1：设定最大进化次数N，iN=0为进化次数变量，子群个数m，im=0为子群计数变量。在每个memeplex中Pb和Pw分别表示性能最好和最坏的青蛙，Pg表示整个种群中最好的青蛙。在每一轮的进化中，改善最坏青蛙Pw的位置。注意，并非对所有青蛙都优化。
4.3.2：调整最坏青蛙的位置，方法如下：
青蛙移动的距离 Di=rand()*(Pb-Pw)
新的位置 Pw=Pw（当前位置）+Di,（Dmax>=Di>=-Dmax）
其中rand()是0-1之间的随机数，Dmax是青蛙移动的最大距离。
4.3.3：如果上述过程能够使得青蛙有一个更好的位置，即能产生一个更好的解，那么就用新的位置青蛙取代原来的青蛙；否则，用Pg代替Pb，重复上述过程。
4.4.4：如果上述方法仍不能生成更好的青蛙，那么就随机生成一个新解取代原来最坏的青蛙Pw。

int mycmp(const void *a, const void *b) {return (*(Individal*)b).value > (*(Individal*)a).value ?1:-1;
}

void memetic()
{int i, j, k, l, n;double a,b;for (n = 0; n<N; n++){for (i = 0; i<M; i++){Individal temp[M];for (j = 0; j<V; j++){temp[i].d[j] = R*(pb[i].d[j] - pw[i].d[j]);temp[i].d[j] = temp[i].d[j] > D ? D : temp[i].d[j];temp[i].d[j] = temp[i].d[j] < -D ? -D : temp[i].d[j];temp[i].d[j] += pw[i].d[j];}temp[i].value = fitness(temp[i]);if (temp[i].value<pw[i].value)// 子群最好的{memeplex[i][0] = temp[i];qsort(memeplex[i], I, sizeof(Individal), mycmp);pw[i] = memeplex[i][0];pb[i] = memeplex[i][I - 1];}else{for (k = 0; k<V; k++){temp[i].d[k] = R*(pg.d[k] - pw[i].d[k]);temp[i].d[j] = temp[i].d[j] > D ? D : temp[i].d[j];temp[i].d[j] = temp[i].d[j] < -D ? -D : temp[i].d[j];temp[i].d[k] += pw[i].d[k];}temp[i].value = fitness(temp[i]);if (temp[i].value<pw[i].value)//整体最好的{memeplex[i][0] = temp[i];qsort(memeplex[i], I, sizeof(Individal), mycmp);pw[i] = memeplex[i][0];pb[i] = memeplex[i][I - 1];}else                     //随机解{for (l = 0; l<V; l++){memeplex[i][0].d[l] = R*(MAX - MIN) + MIN;}memeplex[i][0].value = fitness(memeplex[i][0]);qsort(memeplex[i], I, sizeof(Individal), mycmp);pw[i] = memeplex[i][0];pb[i] = memeplex[i][I - 1];}}}}
}

4.种群迭代

青蛙在memeplex之间跳跃。在每个memeplex中执行了一定的memetic进化之后，将各个子群合并到整体，再重新排序，并更新种群中最好的青蛙Pg
如果迭代终止条件满足，则停止；否则，继续迭代.一般情况下，当执行了一定次数的循环进化，代表最好解的青蛙的位置不再改变的时候，算法停止。

void renew()
{int i, j, k;i = 0;for (j = 0; j<M; j++){for (k = 0; k<I; k++){group[i] = memeplex[j][k];i++;}}
}

外部迭代循环：

	for (int i = 0; i<G; i++){sort();memetic();renew();}

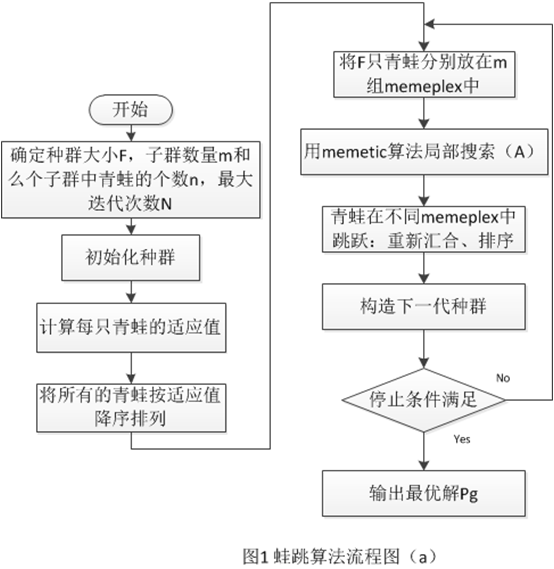
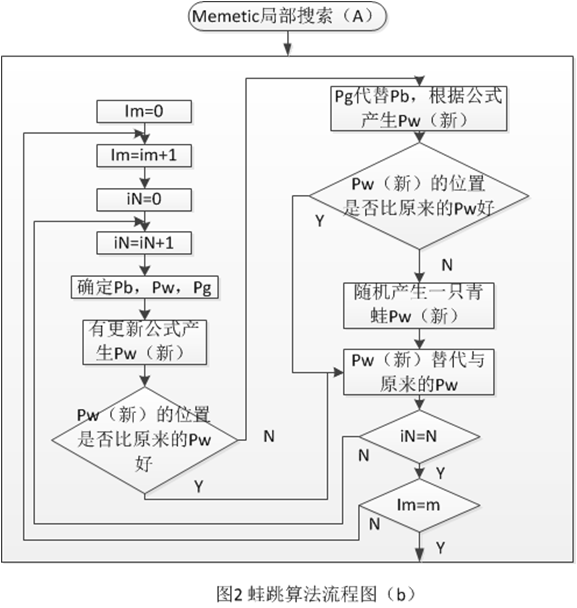
五、参考流程图

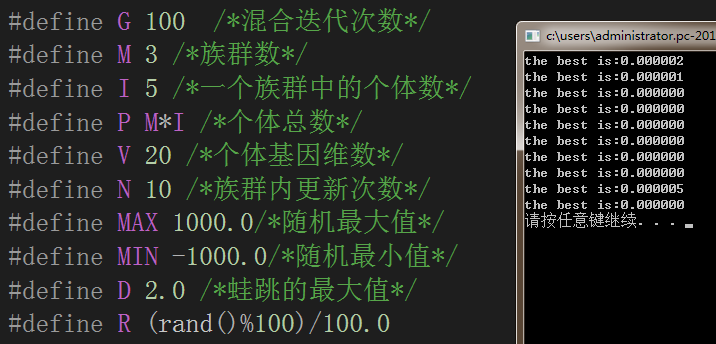
六、测试截图

void test()
{init();for (int i = 0; i<G; i++){sort();memetic();renew();}pg = group[P - 1];printf("the best is:%f\n", pg.value);//for (int i = 0; i<V; i++)//{//	printf("d[(%d)]=%f\n", i, pg.d[i]);//}}void main()
{int n = 10;while (n--){test();}system("pause");
}