本文主要是介绍【蛮力算法和分治法】平面最接近点对(Python),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
问题介绍
问题分析
蛮力法很好理解,遍历所有的点计算其中所有的点之间的距离,并设置一个最小距离数,持续遍历时持续和结果比较,得到最小的距离。
分治算法的思想则是,将大问题分解成小问题分别求解后合并,此处就是如此,将点所在的区域持续的分隔成左右两部分,分别求解,当区域不断被划分,区域中只剩下三个点的时候,采用蛮力法对点之间的距离进行计算。
这样算出来的距离只是其中一半,另一半也如此,随后进行比较得到最小距离,但别忘了,要是距离最短的两个点,一个在左半部分一个在右半部分,那该怎么办?这就是我们的“跨越中线问题”。
中线问题解决思路则是,当左右两边的最小距离(min_distance)求出后,往中线左右各取最小距离范围,即中间带宽的距离为2 * min_distance。之所以是这样的结果,原因是这样能够保证可以取到最小结果的点被包含在带宽而免去其它多余的计算。如果按照这个取,当中间线上有点,这个点和其他的在同一条水平线上的点的距离如果在这个范围,必然比min_distance小,这样的点才有计算的价值,否则必然距离比min_distance大的点放进来只会增加计算量且无用。
时间复杂度上,最开始对点集进行排序,时间复杂度为O(nlogn)。随后的分隔工作采用二分法,假设总的点数量为n,分隔区域的次数为k次,那么2 ^ k = n,则k = log2n。每次分隔后都需要完成合并操作,合并最后的结果比较得出最小值,所以时间复杂度为O(n)。该算法的总时间复杂度为O(nlogn)。
对图的展示采用python中的包,同时,既然要实验观察两者的各个效率,那就需要观察其运行时间,放入多点进去,观察两者时间上的差别。
代码
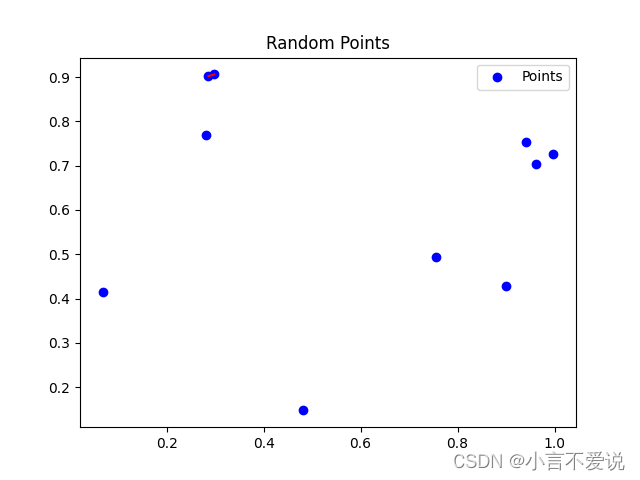
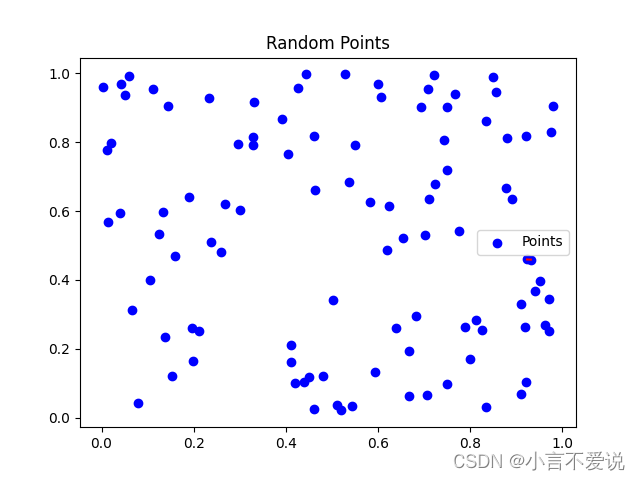
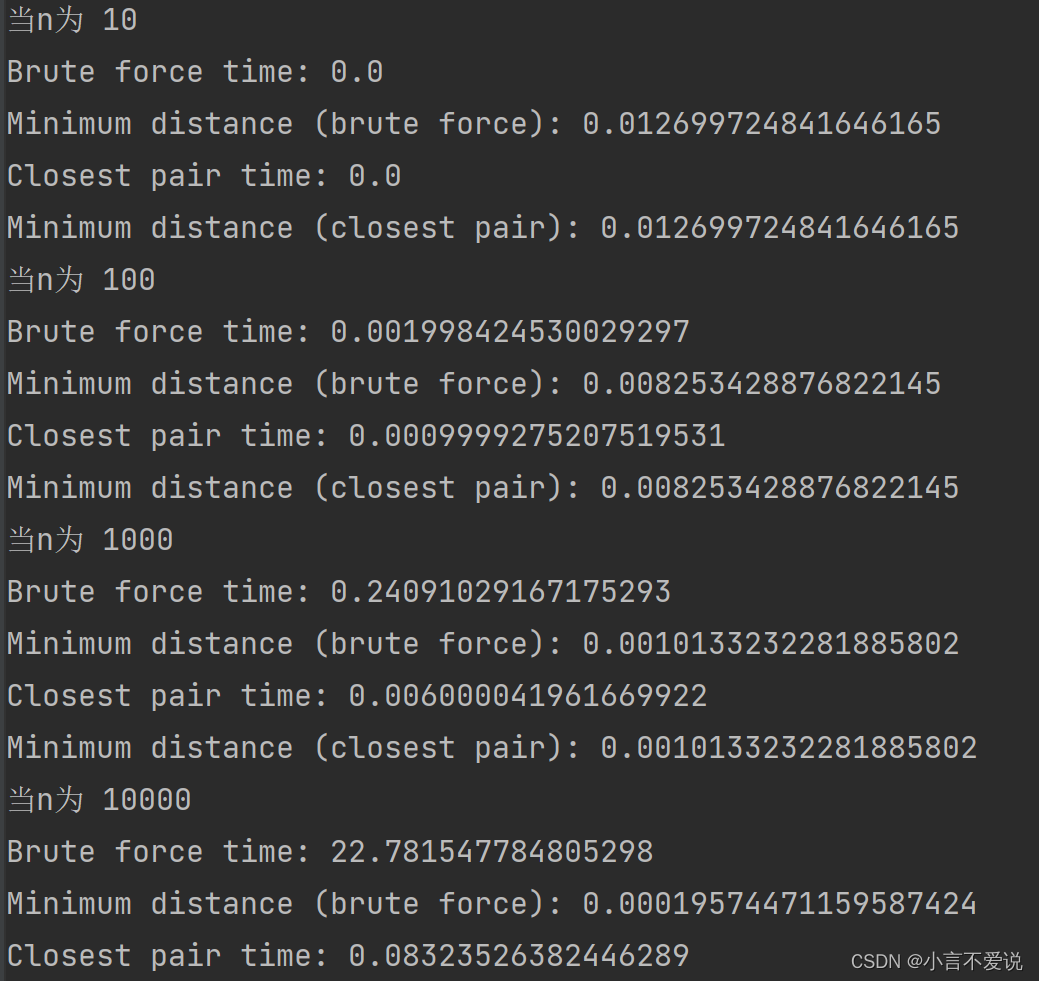
最终可以得到四不同n的四个图,图中的最近点对会用红色的线连接,以及两个算法解决同样数量的点集的时间分别为多少。


import time
import random
import mathfrom matplotlib import pyplot as plt# 生成随机点集
def generate_random_points(n):points = [(random.random(), random.random()) for _ in range(n)]return points# 计算两点之间的距离
def distance(p1, p2):return math.sqrt((p1[0] - p2[0]) ** 2 + (p1[1] - p2[1]) ** 2)# 暴力求解最近点对的距离
def brute_force(points):min_distance = float('inf')for i in range(len(points)):for j in range(i + 1, len(points)):d = distance(points[i], points[j])if d < min_distance:min_distance = dreturn min_distance# 最近点对问题的分治算法
def closest_pair(points):# 根据 x 坐标排序sorted_points = sorted(points, key=lambda x: x[0])return closest_pair_recursion(sorted_points)def closest_pair_recursion(points):n = len(points)if n <= 3:return brute_force(points)mid = n // 2mid_point = points[mid]# 取左右部分left_points = points[:mid]right_points = points[mid:]# 递归处理左右半部分的最近点对距离left_min = closest_pair_recursion(left_points)right_min = closest_pair_recursion(right_points)min_distance = min(left_min, right_min)strip_points = [point for point in points if abs(point[0] - mid_point[0]) < min_distance] # 取中间带宽内的点strip_min = strip_closest(strip_points, min_distance) # 处理中间带宽内的最近点对距离return min(min_distance, strip_min)def strip_closest(strip_points, min_distance):min_distance_strip = min_distancen = len(strip_points) # 获取中间带宽内的点的数量n。for i in range(n):j = i + 1# j小于中间带宽内的点的数量n,并且当前点与下一个点之间的纵坐标差小于最小距离min_distance_strip。while j < n and (strip_points[j][1] - strip_points[i][1]) < min_distance_strip:min_distance_strip = min(min_distance_strip, distance(strip_points[i], strip_points[j]))j += 1return min_distance_strip# 主函数
def main():ns = [10, 100, 1000, 10000]for n in ns:print("当n为", n)points = generate_random_points(n)startTime = time.time()minDistanceBruteForce = brute_force(points)endTime = time.time()timeTaken = endTime - startTimeprint("Brute force time:", timeTaken)print("Minimum distance (brute force):", minDistanceBruteForce)startTime = time.time()minDistanceClosestPair = closest_pair(points)endTime = time.time()timeTaken = endTime - startTimeprint("Closest pair time:", timeTaken)print("Minimum distance (closest pair):", minDistanceClosestPair)# 画出点集x = [point[0] for point in points]y = [point[1] for point in points]plt.figure()plt.scatter(x, y, color='b', label='Points')# 标记最近点对for i in range(len(points)):for j in range(i + 1, len(points)):if distance(points[i], points[j]) == minDistanceClosestPair:plt.plot([points[i][0], points[j][0]], [points[i][1], points[j][1]], color='r')plt.title('Random Points')plt.legend()plt.show()# 执行主函数
if __name__ == "__main__":main()
这篇关于【蛮力算法和分治法】平面最接近点对(Python)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






