Making the Grade 路面修整

2024-01-09 17:59

文章标签 路面 grade making 修整

本文主要是介绍Making the Grade 路面修整，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

「POJ 3666」Making the Grade 路面修整

1 算法标签

dp动态规划，滚动数组优化

2 题目难度

提高/提高+

3 题面

「POJ 3666」Making the Grade 路面修整

4 分析题面

4.1 简要描述

给出数列 $A$ , 求非严格单调不上升或单调不下降, 且 $S=\sum^N_{i=1}|A_i-B_i|$ 最小的序列 $B$ ，输出 $S$

4.2 模型转换

输入N, 然后输入N个数，求最小的改动这些数使之成非严格递增或非严格递减即可

5 问题分析

以B为非严格单调递增为例

考虑已经选了 $n$ 个数

若 $n = 1$ ， $A_1=B_1$ 时 $S$ 最小为 $A_1-B_1|$
若 $n > 1$ ，前面已经选择了 $n - 1$ 个数，取得了最小值，考虑怎么取第 $n$ 个数
- 若 $A_i≥B_{i-1}$ ， $B_i=A_i$ 显然最优
- 若 $A_i<B_{i-1}$ ，
  - $B_i=A_i$
  - 将 $B_k,B_{K+1},...,B_i$ 都赋值为 $A_k,A_k+1,...,A_i$ 的中位数
    口胡证明：
    
    我们可以将 $B_k,B_{K+1},...,B_i$ 标记在数轴上，再将 $A_k,A_k+1,...,A_i$ 标记上
    
    那么，其实 $S$ 的几何含义就是每一组 $A_i$ 到 $B_i$ 的距离之和
    
    我们也学过绝对值问题： $x-k_1|+|x-k_2|+|x-k_3|...$ 的最小值这种
    
    其实和这里的 $S$ 是没有任何区别的
    
    所以，我们知道零点分段法
    
    就是取中位数（就是使每个绝对值内部为0的x答案数组的中位数）
    
    可以使得绝对值之和最小
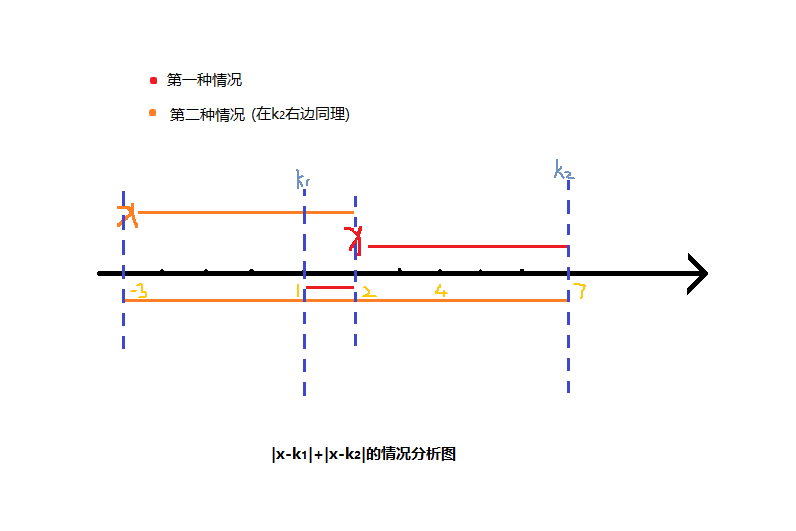
    1. 如果x在两个 $k$ 之间,那么无论x在哪,距离之和都是这两个k的距离
    2. 如果在这两个 $k$ 之外,那么距离之和则为两个k距离加上两倍的x距近的k的距离，肯定小于第一种情况
    那么我们只要尽量让 $x$ 在越多的 $k$ 之间即可
    
    那么最佳x在图中就是 $4$ ,如果 $k$ 的个数为偶数n,则是 $k_{n/2}$ 和 $K_{n/2+1}$ 之间
    
    综上，选择中位数最佳

通过综上分析，我们直接暴力肯定是不行的~~（这个复杂度直接爆掉了）~~

但是！

我们可以得到一个结论：

B数列中的每个数必定都为A数列中的元素

所以，我们可以考虑dp

阶段：到第 $i$ 位

状态： $dp_{i,j}$ 表示以 $B_j$ 结尾的 $S_{min}$

B数组是A的复制排序处理过后的数组

$d p [i] [j]$ 表示把前i个数变成不严格单调递增且第 $i$ 个数变成原来第 $j$ 大的数的最小代价

转移方程： $dp_{i,j}=min(dp_{i-1,j})+|A_i-B_j|,其中1≤j≤n$

6 实现细节

6.1 滚动数组

开二维数组有点浪费欸

那怎么办呢？

由于我们只用到了 $i - 1$

所以，我们考虑用滚动数组优化，用位运算符&来记录，这样就只用了 $0 / 1$ 来表示，重复利用，节省空间

$i$ & $1$ 的效果和 $i$ % $2$ 的效果是一样的，但是 $i$ & $1$ 要快一点

且这种方式比直接写0/1少了一个不断交换的过程

~~窝jio得这个还是很香的~~

将 $i - > i$ & $1$ ， $i - 1 - > (i - 1)$ & $1$

方程就变成了这样：

$d p [i$ & $1] [j] = m i n (d p [(i - 1)$ & $] [k]) + ∣ A [i] - B [j] ∣, 其中 1 \leq j \leq n, 1 \leq k \leq j$

6.2 最小值

但是这个复杂度。。

看上去好像是3层循环，就是 $O(n^3)$ 啊

在 $n < = 2000$ 的时候就已经game over了，显然不行啊

这个问题应该有手就行吧

其实只要一边更新 $m i n (f [i - 1] [k])$ 一般算当前的 $f [i] [j]$ 就行

~~（因为 $k$ 只到 $j$ ）~~

6.3 降序

不严格单调不上升的情况也一样

更加方便的是可以把 $B$ 数组从大到小排序后，做单调不下降的dp就🆗了

7 代码实现（增加代码注释）

#include<bits/stdc++.h>
using namespace std;
const int N=2e4+2;
int n,f[2][N],a[N],b[N],ans=0x3f3f3f3f;
bool cmp1(int x,int y){return x<y;
}//升序 
bool cmp2(int x,int y){return x>y;
}//降序 
void work(){for(int i=1;i<=n;i++){f[1][i]=abs(a[1]-b[i]);}//边界条件for(int i=2;i<=n;i++){int minn=f[(i-1)&1][1];for(int j=1;j<=n;j++){minn=min(minn,f[(i-1)&1][j]);//边更新边求f[i&1][j]=minn+abs(a[i]-b[j]);//滚动数组 }} for(int i=1;i<=n;i++){ans=min(ans,f[n&1][i]);}//求答案
}
int main(){scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d",&a[i]);b[i]=a[i];//拷贝到b数组}sort(b+1,b+1+n,cmp1);//从小到大 work(); //dp计算sort(b+1,b+1+n,cmp2);//从大到小 work();//直接就是一样的啊printf("%d",ans);//输出最小return 0;
}