本文主要是介绍Python - 深夜数据结构与算法之 剪枝,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
一.引言
二.剪枝的简介
1.初级搜索方式
2.高级搜索方式
3.搜索模版回顾
4.剪枝
三.经典算法实战
1.Climbing-Stairs [70]
2.Coin-Change [322]
3.Generate-Parentheses [22]
4.N-Queens [51]
5.Valid-Sudoku [36]
6.Sudoku-Solver [37]
四.总结
一.引言
剪枝对应为检索的优化,最基本的检索例如 DFS、BFS,而剪枝的主要目的则是减少无用的搜索,提高算法效率,下面我们看下常用的剪枝策略与实现方法。
二.剪枝的简介
1.初级搜索方式

初级搜索主要包含 DFS 深度优先以及 BFS 广度优先,其利用编程语言自带的递归方式或者 Stack、Dequeue 实现,我们前面的题目用到了很多次。由于其是暴力或者遍历的搜索,时间复杂度相对较高,所以经常需要进行优化,最常见的优化就是不重复,我们可以构建一个 Cache、Memo 缓存结果例如 Fib,也可以增加判断条件例如括号生成的左右括号数量限制。
2.高级搜索方式
◆ 双向 BFS
BFS 广度优先遍历会优先找自己周围的元素,而双向 BFS 则是从起点和终点同时 BFS 搜索,最终在中间位置相遇,提高搜索的效率。
◆ 启发式搜索
启发式搜索又叫 A* 搜索,它的实现基于优先级队列即 Priority-Queue,其不拘泥于 DFS、BFS,而是根据每个状态分叉的优先级决定下一步走哪里,走哪里可能的收益更高。
3.搜索模版回顾
◆ DFS - 递归

◆ DFS - 非递归

◆ BFS - 栈

◆ 分治-回溯
通过分治的方法寻找可能的答案,如果答案不对则回退 1 步或者 N 步,到原有的状态继续探索新的路径。

4.剪枝
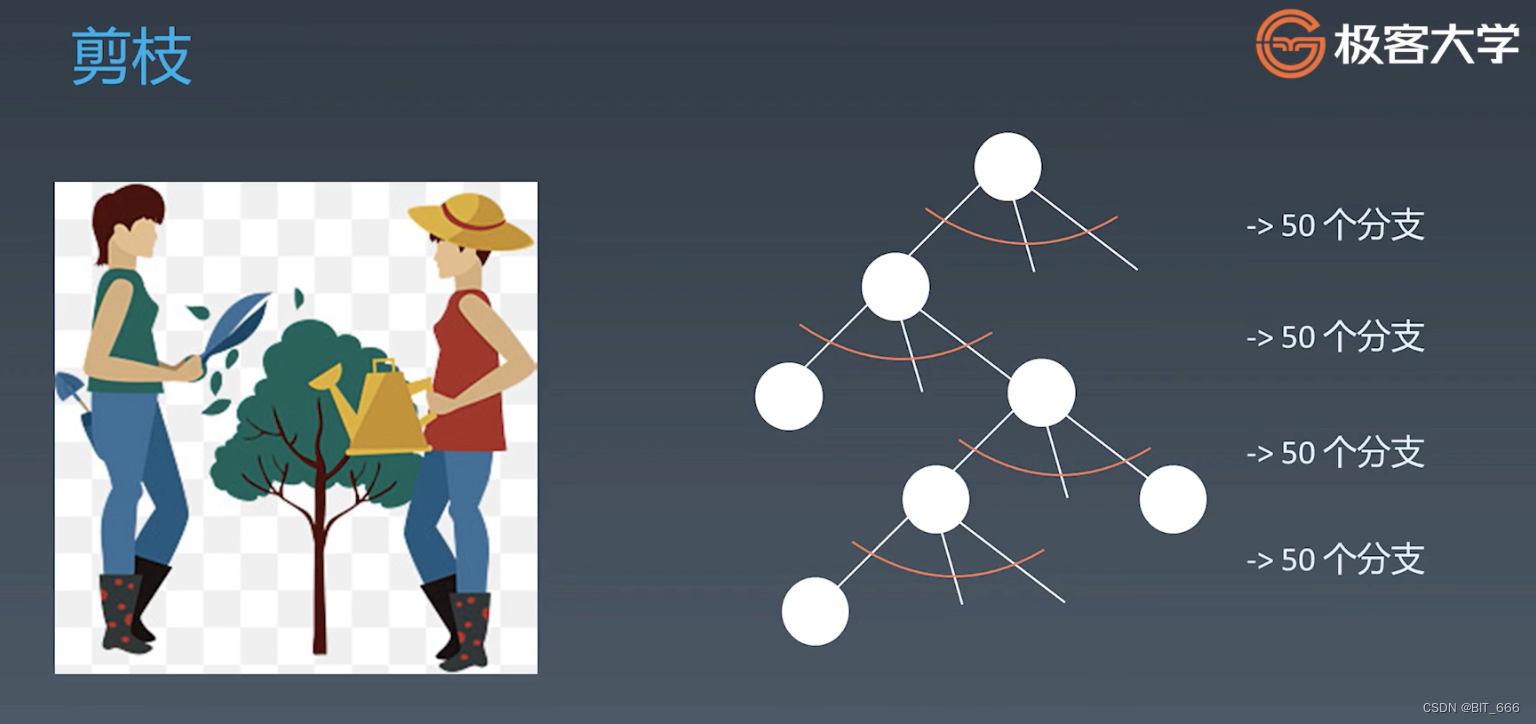
当我们对应问题生成其状态树时,我们可以通过 Cache 的方法,避免重复计算,从而减少分支的计算,或者判断当前的分支不够好,我们也可以剪枝避免多余的计算。
三.经典算法实战
1.Climbing-Stairs [70]
爬楼梯: https://leetcode-cn.com/problems/climbing-stairs/

◆ 题目分析
爬楼梯每次可以走 1 步也可以走 2 步,对应 F(n) = F(n-1) + F(n-2),所以可以转换为 Fib,这里我们不嫌重复,再次用三种方法实现下 Fib,主要是感受剪枝的常规操作。
◆ 暴力递归
class Solution(object):def climbStairs(self, n):""":type n: int:rtype: int"""if n == 0 or n == 1:return 1return self.climbStairs(n-1) + self.climbStairs(n-2)
◆ 递归 + Cache
class Solution(object):def __init__(self):self.dic = {1:1, 2:2}def climbStairs(self, n):""":type n: int:rtype: int"""if n not in self.dic:self.dic[n] = self.climbStairs(n-1) + self.climbStairs(n-2)return self.dic[n]这里主要温习 cache 的写法,把直接要返回的值放到 cache 里,再返回 cache。
◆ DP Table
class Solution(object):def climbStairs(self, n):""":type n: int:rtype: int"""if n <= 2:return na, b, c = 1, 2, 3# 滑动数组for i in range(3, n):a, b, c = b, c, b+creturn c
2.Coin-Change [322]
零钱兑换: https://leetcode.cn/problems/coin-change/

◆ 题目分析
以 1、2、5 为状态空间构建可能得状态树,寻找路径最短达到 target 金额的,就是最少的硬币数。
◆ 暴力递归
class Solution(object):def coinChange(self, coins, amount):""":type coins: List[int]:type amount: int:rtype: int"""# 给定目标金额,所需最少金币数量def dp(n):if n == 0:return 0if n < 0 :return -1# 结果res = float('inf') for coin in coins:sub = dp(n - coin)# 无解跳过,因为钱大不够找零if sub == -1: continue# 子问题 + coin = Amonut,所以子问题的 dp + 1 = Amount 的数量res = min(sub + 1, res)return res if res != float('inf') else -1return dp(amount)又又又超时啦,根据状态树可以看到时间复杂度是 o(k * n^k) 的,k 是 3 种取值,n^k 则是下面分叉找结果。下面尝试 Cache 优化。

◆ 递归 + Cache
class Solution(object):def coinChange(self, coins, amount):""":type coins: List[int]:type amount: int:rtype: int"""cache = {}# 给定目标金额,所需最少金币数量def dp(n):if n in cache:return cache[n]if n == 0:return 0if n < 0 :return -1# 结果res = float('inf') for coin in coins:sub = dp(n - coin)# 无解跳过,因为钱大不够找零if sub == -1: continue# 子问题 + coin = Amonut,所以子问题的 dp + 1 = Amount 的数量res = min(sub + 1, res)cache[n] = res if res != float('inf') else -1return cache[n]return dp(amount)cache 的套路写法,在返回值处记录参数与 return 值的关系,在开头处判断参数是否在 cache 中。慢悠悠的过啦 !
◆ DP Table
class Solution(object):def coinChange(self, coins, amount):""":type coins: List[int]:type amount: int:rtype: int"""# 初始化状态空间 # 凑 amount 至少可以是 amonut x 1 枚硬币# 初始化一个比 amount 大的值都可以,这里也可以 float('inf') dp = [amount + 1] * (amount + 1)dp[0] = 0# 外循环遍历所有状态值for state in range(len(dp)):# 内循环求最小值for coin in coins:# 子问题无解 跳过if state - coin < 0: continuedp[state] = min(dp[state], dp[state - coin] + 1)return dp[amount] if (dp[amount] != amount + 1) else -1将递归的形式转换为 DP 形式。
◆ DP Table 优化
class Solution(object):def coinChange(self, coins, amount):""":type coins: List[int]:type amount: int:rtype: int"""# 初始化一个较大的值dp = [amount + 1] * (amount + 1)dp[0] = 0for coin in coins: # 遍历硬币for j in range(coin, amount + 1):dp[j] = min(dp[j], dp[j-coin] + 1) # DP 方程ans = dp[amount]return ans if ans != amount + 1 else -1上面判断了很多次 Coin 和 State 的关系,我们可以转换一下 for 循环顺序,对于 coin,只判断 coin - len(dp) 的范围即可,因为小的部分都被 amonut - coin < 0 找不开过滤掉了,所以这里进行了一层剪枝。这里给出了四个方法,我们从暴力到 Cache,Cache 到 Dp,最后到 DP 剪枝,大家可以好好体会下这个优化的过程。
3.Generate-Parentheses [22]
括号生成: https://leetcode.cn/problems/generate-parentheses/

◆ 题目分析
本题如果不剪枝的情况下,n 个位置都有左右括号两种情况,时间复杂度是 2^n 指数级别,通过增加 left 和 right 剪枝,提高程序效率,下面在 DFS 和 BFS 的基础上进行剪枝。
◆ BFS
class Solution(object):def generateParenthesis(self, n):""":type n: int:rtype: List[str]"""res = []queue = [("", 0, 0)]while queue:cur, left, right = queue.pop(0)if left == right == n:res.append(cur)if left < n:queue.append((cur + "(", left + 1, right))if right < left:queue.append((cur + ")", left, right + 1))return res
◆ DFS
class Solution(object):def generateParenthesis(self, n):""":type n: int:rtype: List[str]"""# 保存结果result = []self.generate(0, 0, n, "", result)return resultdef generate(self, left, right, n, s, result):if left == n and right == n:result.append(s)# 保证最左边一定是 '('if left < n:self.generate(left + 1, right, n, s + "(", result)# right 不够就补充if right < left:self.generate(left, right + 1, n, s + ")", result)
4.N-Queens [51]
N 皇后: https://leetcode.cn/problems/n-queens/description/
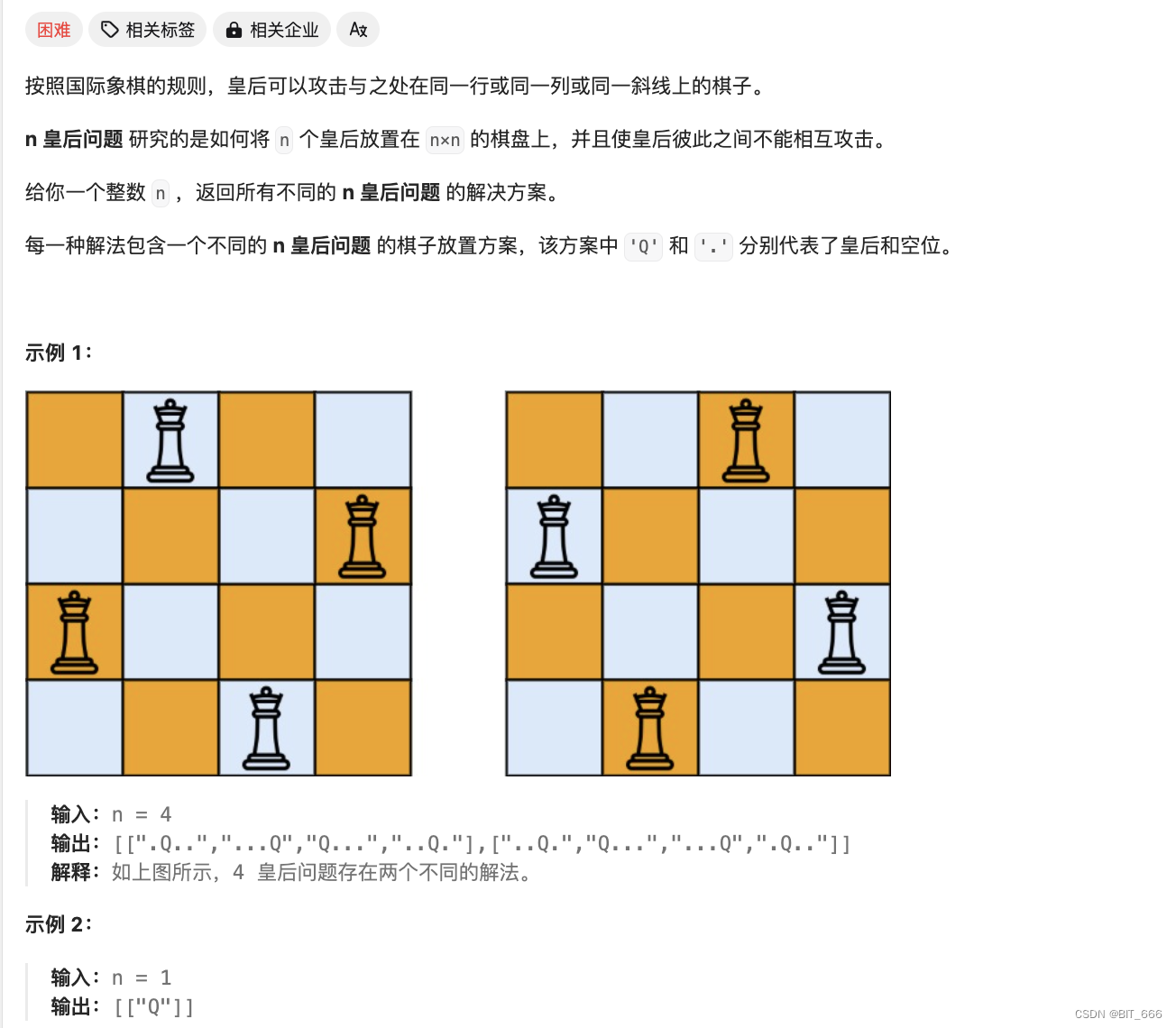
◆ 题目分析
本题和上面括号生成类似,但是棋盘的复杂度提高了,每个棋子每行有 n 个位置,下一个棋子 n-1 个位置,最后的时间复杂度为 o(n!),通过增加 col、pie、na 三个方向的剪枝,提高算法的执行效率。
◆ DFS
class Solution(object):def solveNQueens(self, n):""":type n: int:rtype: List[List[str]]"""results = []# 行 左 右 是否可以放置cols = set()pie = set()na = set()def dfs(n, row, cur):if row >= n:results.append(cur)for col in range(n):if col in cols or (row + col) in pie or (row - col) in na:continue# 判断有效cols.add(col)pie.add(row + col)na.add(row - col)dfs(n, row + 1, cur + [col])# 恢复状态cols.remove(col)pie.remove(row + col)na.remove(row - col)dfs(n, 0, [])return self.genResult(n, results)def genResult(self, n, results):return [[ '.' * i + 'Q' + (n - i - 1) * '.' for i in result] for result in results]def genResultV2(self, n, results):re = []for result in results:re.append([ '.' * i + 'Q' + (n - i - 1) * '.' for i in result])return re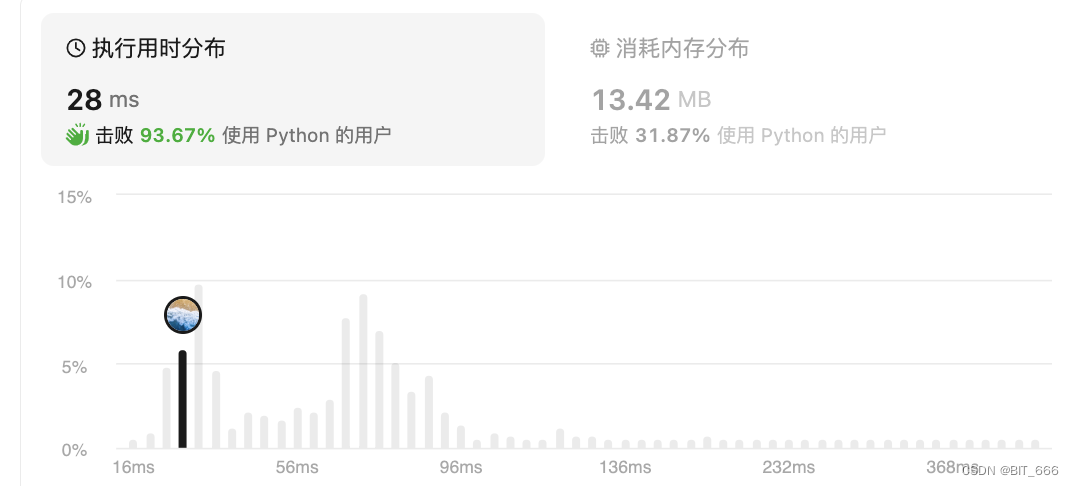
5.Valid-Sudoku [36]
有效数独: https://leetcode.cn/problems/valid-sudoku/description/

◆ 题目分析
像 N 皇后一样,判断每行、每列是否有重复,再判断每一个 3x3 的区域是否重复。行列很好判断,剩下就是确定每一个方格区域,我们先通过测试得到根据 [i,j] 位置获取分区的代码:
import numpy as npnums = []for i in range(9):for j in range(9):location = (i // 3) * 3 + j // 3nums.append(location)nums = np.array(nums).reshape(9, 9)print(nums)
所以 location = (i // 3) * 3 + j // 3 就是我们获取元素分区的方法,这样顺序遍历即可。
◆ 遍历实现
class Solution(object):def isValidSudoku(self, board):""":type board: List[List[str]]:rtype: bool"""# 获取分区: location = (i // 3) * 3 + j // 3row_set = [[] for _ in range(9)]col_set = [[] for _ in range(9)]location_set = [[] for _ in range(9)]for row in range(9):for col in range(9):cur_val = board[row][col]# 未填写位置过滤if cur_val == ".":continue# 行if cur_val not in row_set[row]:row_set[row].append(cur_val)else:return False# 列if cur_val not in col_set[col]:col_set[col].append(cur_val)else:return False# 区块location = (row // 3) * 3 + col // 3if cur_val not in location_set[location]:location_set[location].append(cur_val)else:return Falsereturn Trueif __name__ == '__main__':s = Solution()board = [["5", "3", ".", ".", "7", ".", ".", ".", "."],["6", ".", ".", "1", "9", "5", ".", ".", "."],[".", "9", "8", ".", ".", ".", ".", "6", "."],["8", ".", ".", ".", "6", ".", ".", ".", "3"],["4", ".", ".", "8", ".", "3", ".", ".", "1"],["7", ".", ".", ".", "2", ".", ".", ".", "6"],[".", "6", ".", ".", ".", ".", "2", "8", "."],[".", ".", ".", "4", "1", "9", ".", ".", "5"],[".", ".", ".", ".", "8", ".", ".", "7", "9"]]print(s.isValidSudoku(board))
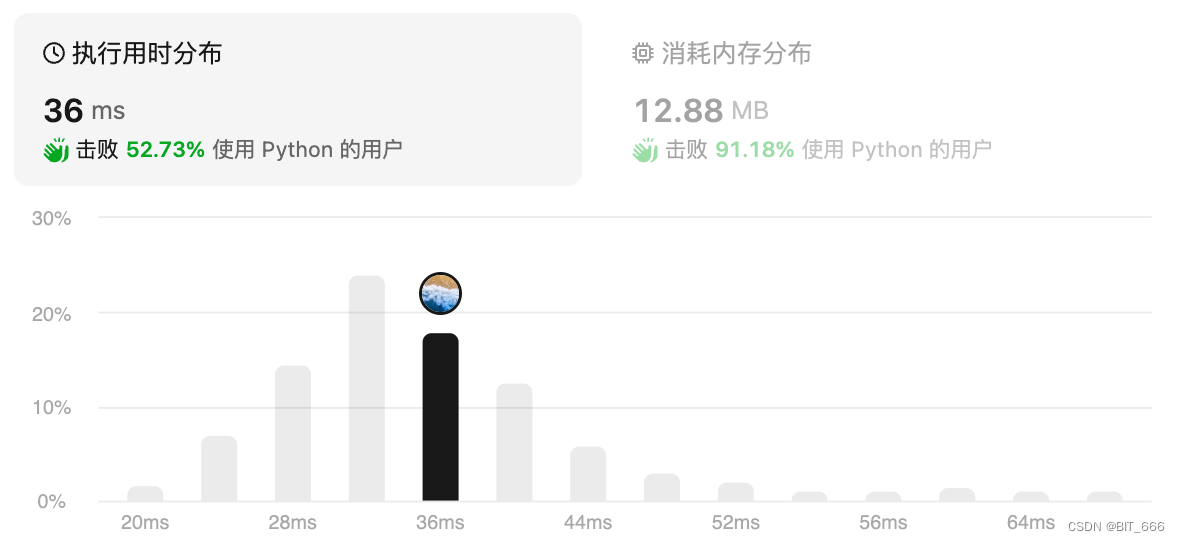
只需要一次遍历,对每一个非 '.' 的字段判断其是否在对应的集合中,有重复则退出,类似 N 皇后一样,相同的数字不能相遇。这道题我们主要学会 location = (i // 3) * 3 + j // 3 这个是我们本题最大的收获。
6.Sudoku-Solver [37]
解数独: https://leetcode.cn/problems/sudoku-solver/description/

◆ 遍历实现
上面已经实现了如何判断一个数独棋盘是否有效,我们只需要在每一个位置尝试可以使用的数字,然后 DFS 或者 BFS 推进,如果能够把表格填满且判断 isValid == True,则数独解答完毕。
◆ DFS
class Solution:def solveSudoku(self, board):"""Do not return anything, modify board in-place instead."""self.backtracking(board)def backtracking(self, board):# 若有解,返回True;若无解,返回Falsefor i in range(len(board)): # 遍历行for j in range(len(board[0])): # 遍历列# 若空格内已有数字,跳过if board[i][j] != '.': continuefor k in range(1, 10): if self.is_valid(i, j, k, board):board[i][j] = str(k)if self.backtracking(board): return Trueboard[i][j] = '.'# 若数字1-9都不能成功填入空格,返回False无解return Falsereturn True # 有解def is_valid(self, row, col, val, board):# 判断同一行是否冲突for i in range(9):if board[row][i] == str(val):return False# 判断同一列是否冲突for j in range(9):if board[j][col] == str(val):return False# 判断同一九宫格是否有冲突start_row = (row // 3) * 3start_col = (col // 3) * 3for i in range(start_row, start_row + 3):for j in range(start_col, start_col + 3):if board[i][j] == str(val):return Falsereturn True

◆ DFS 剪枝
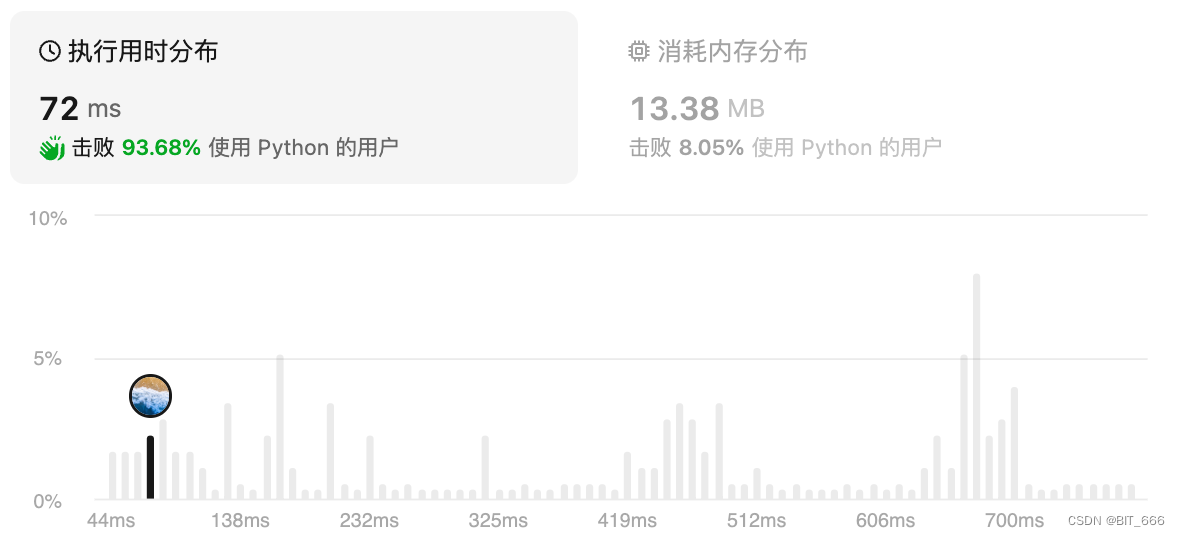
class Solution(object):def solveSudoku(self, board):""":type board: List[List[str]]:rtype: None Do not return anything, modify board in-place instead."""valid_row = [set(range(1, 10)) for _ in range(9)] # 行可用数字valid_col = [set(range(1, 10)) for _ in range(9)] # 列可用数字valid_block = [set(range(1, 10)) for _ in range(9)] # 块可用数字# 待填区域candidate = []for row in range(9):for col in range(9):# 更新当前 row、col 可用数字cur_val = board[row][col]if cur_val != ".":cur_val = int(cur_val)valid_row[row].remove(cur_val)valid_col[col].remove(cur_val)cur_block = (row // 3) * 3 + col // 3valid_block[cur_block].remove(cur_val)else:# 追加待填区域坐标candidate.append((row, col))self.backtrack(candidate, 0, board, valid_row, valid_col, valid_block)return boarddef backtrack(self, _candidate, position, board, valid_row, valid_col, valid_block):if position == len(_candidate):return True# 获取当前代填位置信息row, col = _candidate[position]block = (row // 3) * 3 + col // 3# 三个交集获取当前位置可用元素for val in valid_row[row] & valid_col[col] & valid_block[block]:valid_row[row].remove(val)valid_col[col].remove(val)valid_block[block].remove(val)# Process: 判断可行性board[row][col] = str(val)# Drill Down: 下一层if self.backtrack(_candidate, position + 1, board, valid_row, valid_col, valid_block):return True# Restore: 恢复状态board[row][col] = "."valid_row[row].add(val)valid_col[col].add(val)valid_block[block].add(val)return False上面的 DFS 从 range(1-10) 分别尝试,但是我们可以通过 set 缓存提前得知当前位置的可用数字从而缩减检索范围。时间复杂度降低,但是因为额外使用了 3 个 List[Set()],所以空间复杂度较高。这里也遵循前面讲到的递归回朔的执行顺序,Process -> Drill Down -> Restore。
四.总结
这里带来剪枝的一些经典算法例题,可以看到剪枝可以大幅提高程序执行的效率,其思想是尽量避免重复工作或者无意义的探索。除了剪枝外,还有另外一种搜索中常用的高级搜索方法即双向 BFS,其思想则是左右开弓,提高逼近答案的速度,后面我们介绍双向 BFS 的思想与题目。
这篇关于Python - 深夜数据结构与算法之 剪枝的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







