When Will You Arrive Estimating Travel Time Based on Deep Neural Networks

本文主要是介绍When Will You Arrive Estimating Travel Time Based on Deep Neural Networks，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. 背景

这是一篇发表在2018AAAI上面的文章，其目的是通过对历史车辆轨迹的学习，然后用于预测车辆的通勤时间(Travel Time Estimation)，也就是给定一条路径，然后预测从起点到终点所需要的时间。

在先前的论文中，对于一条路径travel time的预测主要有两种方式：Individual vs. Collective，也就是单独预测和整体预测。所谓单独预测就是将整个路径划分为若干个连续片段，并且预测每个部分的travel time，最后将所有的travel time相加作为整个路径的travel time。而整体预测则是直接预测整个travel time 不再进行分割。单独预测的优点在于能够准确的预测每个部分的travel time，但缺点在于不能够处理复杂的交通情况，例如包含十字路口、红绿灯、转向操作等；同时也不能很好的考虑到各个片段之间在空间和时间上的依赖关系。整体预测的缺点在于数据的稀疏性，因为预测路径越长，到后面轨迹点越少（对于这句话我也不是特别理解，原文如下：）。

However, as the length of a path increases, the number of trajectories traveling on the path decreases, which reduces the confidence of the travel time (derived from few drivers), pointing out that longer path is harder to estimate. Moreover, in many cases, there is no trajectory passing the entire path

因此，作者在这篇论文中选择的是将这两种方法结合起来。

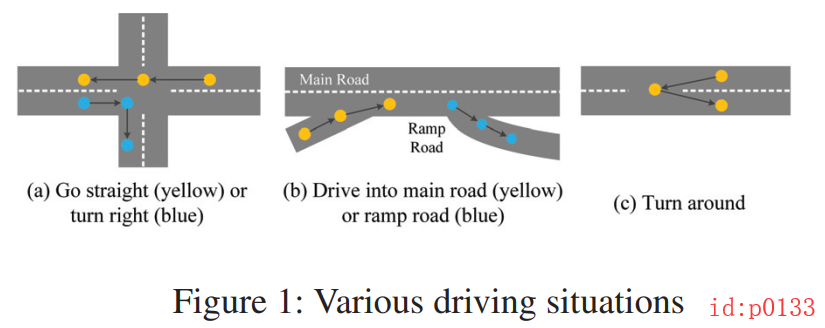
接着，如图p0133(a)所示，在现实情况中每个轨迹的都可能伴随着不同的情况（直行、转弯、转向等）。而想要直接地来提取这些特征显然是困难的。同时，这些空间上的特征分布还伴随着时间上的变换。以图p0133(b)为例，在高峰时期，从主路上的速度快而辅路上的速度慢，因此从辅路进入主路耗时较多，从主路进入辅路耗时较少；而在非高峰时段，进入主路的时间会相对减少。其实还可以举出另外一个例子，在上下班高峰期和非高峰期，通过同一段路程的时间肯定是不一样的。

从作者的分析的确可以看出，这种轨迹数据的确在空间和时间上确实有着不同的特征分布，符合时空数据的特征。因此看到这儿，论文的所提出的模型中自然就是少不了CNN和RNN这两大利器了。可是该怎么通过CNN来刻画轨迹点空间上的特征呢？同样的，时序特征又该怎么用上（或者说套上）RNN呢? 我们知道，在以往的人流（订单需求）预测模型中，大多数都是进行网格划分，然后将轨迹点（需求量）映射到网格中，然后进行CNN处理。可是，在面对这种“点”与“点”之间有着序列关系的情况中显然是不能是这样。

2. 网络模型

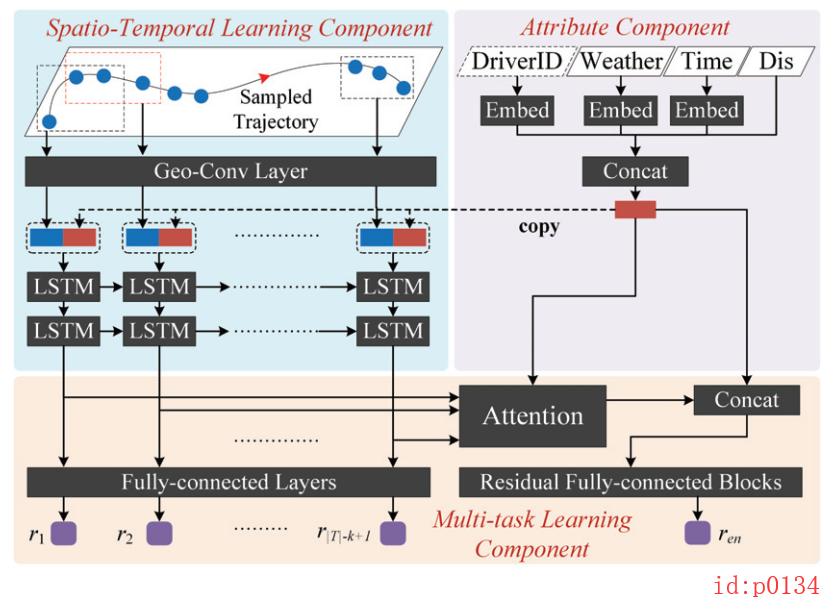
整个网络结构如下图p1034所示，主要包括三个部分：主要部分（Spatio-Temporal Learning Component）以及两个部分（Attribute Component 和 Multi-task Learning Component）。

2.1 数据处理及问题定义

数据处理：

首先，将原始的GPS数据（以时间频率采样）重新以距离进行采样，相邻两个点之间的距离大约在200-400米。这样做的原因是为了避免这样一个问题：模型最终学到的映射只是通过简单的统计轨迹点的个数，然后乘以时间频率就得出了总的travel time，以至于无法预测新样本。最终，对于每个样本来说都是一串以距离采样的轨迹点序列（ $T=\{p_1,\cdots,p_{T}\}$ ）；其中对于每个轨迹点包含的信息有：维度（ $p_i.lat$ ）、经度（ $p_i.lng$ ）和时间戳（ $p_i.ts$ ），而对于一个样本来说，包含的信息有：天气编号（weatherID）、司机编号（driver ID）、周编号（weekID）和时间编号（timeID）。

注：时间戳是指一个时间片（1天划分为1440个时间片，一分钟为一个时间片）
问题定义：

根据给定起点与终点（以及相关的external factors），然后预测整个所需的travel time。

2.2 Attribute Component

这部分主要是用来拟合一些额外的需要注意的因素，包括：天气编号（weatherID）、司机编号（driver ID）、周编号（weekID）和时间编号（timeID），如图p0135所示。同时，由于以上这4种类型的原始数据都是categorical value；因此，在处理的时候加入了Embedding方法，即每个类型值都将从 $v\in[V]$ 被映射为 $R^{E\times 1}$ 。

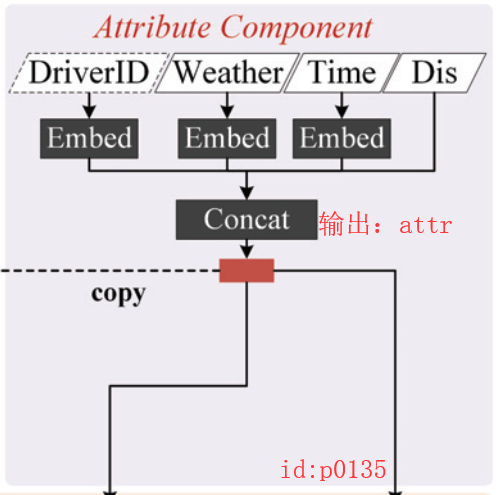
同时，这部分还加入了另外一个比较重要的因素：起始地和目的地之间的距离 $\Delta d_{p_a\rightarrow p_b}$ 。其计算规则为将 $a, b$ 两点之间所有的distance gap相加：
$\Delta d_{p_a\rightarrow p_b}=\sum_{i=a}^{b-1}Dis(p_i,p_{i+1})$
最后，将各个部分的进行concatenate作为整个Attribute Component模块的输出，即向量 $a t t r$ 为输出。

2.3 Spatio-Temporal Component

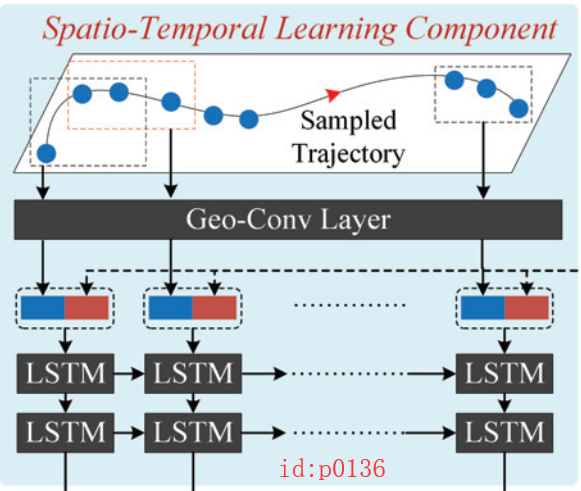
这一部分作为整个网络模型的核心，主要分为两个部分如图p0136所示：Geo-Conv Layer和Recurrent Layer。很明显，这两部分分别用来刻画数据空间上和时间上的特征分布。

Geo-Conv Layer

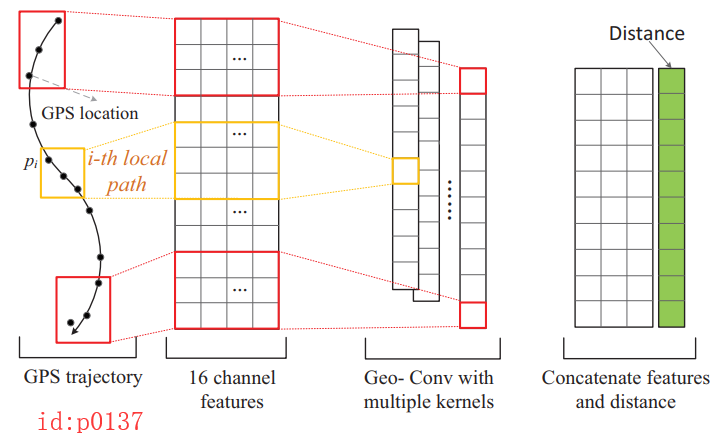
如图p0137所示，该部分首先将一段包含有 $T$ 个点的轨迹坐标，经过一个非线性变换将每个点都映射成一个16维的向量。例如：原始轨迹有12个点，也就是shape为[12,2]经过非线性变换后loc_i的shape为:[12,16].
$loc_i=tanh(W_{loc} \cdot[p_i.lat\circ p_i.lng]),loc_i\in R^{16}\;,loc\in R^{|T|\times 16}$