数学建模学习（90）：Jaya优化算法对多元函数寻优

一、算法介绍

算法步骤：

1. 首先初始化种群个体数量，确定每个个体长度以及终止判据
2. 找到当前种群下的最优个体 best 和最差个体 worst
3. 遍历所有个体，根据公式(1)更新个体参数
   

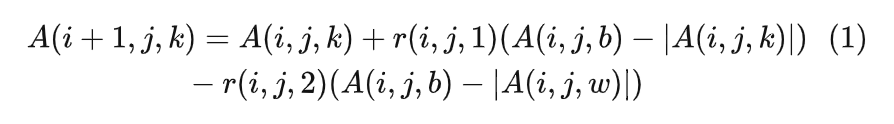
其中，i，j，k分别代表迭代代数，个体的某变量，种群中某个体。该公式是Jaya算法的核心

4. 判断更新后的个体是否优于更新前的个体，若是，则更新个体，否则保留原个体到下一代
5. 判断当前最优个体是否满足终止判据，若是则结束程序，否则遍历步骤2-4

二、 案例实现（一）

2.1 目标函数

第一步：导入模块

import numpy as np# Jaya
from pyMetaheuristic.algorithm import victory
from pyMetaheuristic.utils import graphs

第二步：目标函数设置

def easom(variables_values = [0, 0]):x1, x2     = variables_valuesfunc_value = -np.cos(x1) * np.cos(x2) * np.exp(-(x1 - np.pi) ** 2 - (x2 - np.pi) ** 2)return func_valueplot_parameters = {'min_values': (-5, -5),'max_values': (5, 5),'step': (0.1, 0.1),'solution': [],'proj_view': '3D','view': 'notebook'
}
graphs.plot_single_function(target_function = easom, **plot_parameters)

如下：

2.2 算法实现

第三步：设置算法参数

# jaya - Parameters
parameters = {# 该参数50左右'size': 50,'min_values': (-5, -5),'max_values': (5, 5),# 迭代次数'iterations': 500,'verbose': True
}

第四步：执行算法

jy = victory(target_function = easom, **parameters)

第五步：获取算法最优解

variables = jy[:-1]
minimum   = jy[ -1]
print('变量值为： ', np.around(variables, 4) , ' 最小值为: ', round(minimum, 4) )

如下：

变量值为：  [3.1258 3.1804]  最小值为:  -0.9974

第六步：可视化最优值

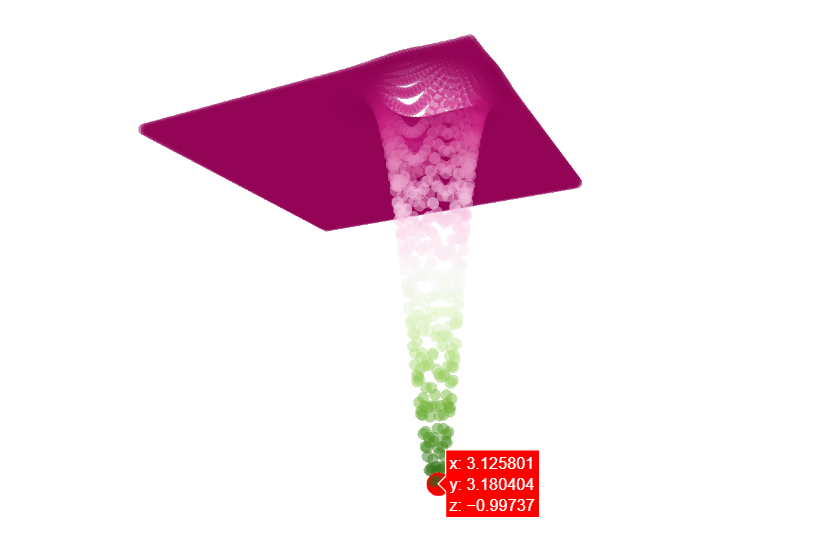
三、案例（二）

我们换一个目标函数,以五维球形函数的最优化计算为例子.

def easom(variables_values):x    = variables_valuesfunc_value = y=sum(x**2 for x in variables_values)return func_value

后续参数类似。。不再重复演示。

四、额外补充

4.1 封装代码

如果你希望改进该算法模块，可以研究修改以下代码：

# Required Libraries
import numpy  as np
import random
import os############################################################################# Function
def target_function():return############################################################################# Function: Initialize Variables
def initial_position(size = 5, min_values = [-5,-5], max_values = [5,5], target_function = target_function):position = np.zeros((size, len(min_values)+1))for i in range(0, size):for j in range(0, len(min_values)):position[i,j] = random.uniform(min_values[j], max_values[j])position[i,-1] = target_function(position[i,0:position.shape[1]-1])return position# Function: Updtade Position by Fitness
def update_bw_positions(position, best_position, worst_position):for i in range(0, position.shape[0]):if (position[i,-1] < best_position[-1]):best_position = np.copy(position[i, :])if (position[i,-1] > worst_position[-1]):worst_position = np.copy(position[i, :])return best_position, worst_position# Function: Search
def update_position(position, best_position, worst_position, min_values = [-5,-5], max_values = [5,5], target_function = target_function):candidate = np.copy(position[0, :])for i in range(0, position.shape[0]):for j in range(0, len(min_values)):a  = int.from_bytes(os.urandom(8), byteorder = "big") / ((1 << 64) - 1)b  = int.from_bytes(os.urandom(8), byteorder = "big") / ((1 << 64) - 1)candidate[j] = np.clip(position[i, j] + a * (best_position[j] - abs(position[i, j])) - b * ( worst_position[j] - abs(position[i, j])), min_values[j], max_values[j] )candidate[-1] = target_function(candidate[:-1])if (candidate[-1] < position[i,-1]):position[i,:] = np.copy(candidate)return position############################################################################# Jaya Function
def victory(size = 5, min_values = [-5,-5], max_values = [5,5], iterations = 50, target_function = target_function, verbose = True):    count              = 0position           = initial_position(size, min_values, max_values, target_function)best_position      = np.copy(position[0, :])best_position[-1]  = float('+inf')worst_position     = np.copy(position[0, :])worst_position[-1] = 0while (count <= iterations): if (verbose == True):print('Iteration = ', count,  ' f(x) = ', best_position[-1])position                      = update_position(position, best_position, worst_position, min_values, max_values, target_function)best_position, worst_position = update_bw_positions(position, best_position, worst_position)count                         = count + 1     return best_position 

4.2 算法论文

http://www.growingscience.com/ijiec/Vol7/IJIEC_2015_32.pdf