MATLAB - MPC - 优化问题（Optimization Problem）

本文主要是介绍MATLAB - MPC - 优化问题（Optimization Problem），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

系列文章目录

前言

模型预测控制可在每个控制间隔内解决一个优化问题，具体来说就是二次规划(QP)。求解结果决定了被控对象在下一个控制间隔之前使用的操纵变量（MV）。

该 QP 问题具有以下特点：

目标或 "成本 "函数 - 要最小化的控制器性能的非负标量。
约束条件 - 解决方案必须满足的条件，如 MV 和被控对象输出变量的物理边界。
决策 - 在满足约束条件的同时使成本函数最小化的 MV 调整。

下文将详细介绍这些功能。

一、标准代价函数

标准成本函数是四个项的总和，每个项都侧重于控制器性能的一个特定方面，如下所示：

$J(z k)=J_{y}(z k)+J_{u}(z k)+J_{\Delta u}(z k)+J_{e}(z k).$

这里，zk 是 QP 决策。如下所述，每个项都包含权重，可帮助您平衡相互竞争的目标。虽然 MPC 控制器提供了默认权重，但您通常需要对其进行调整，以适应您的应用。

1.1 输出参考跟踪

在大多数应用中，控制器必须将选定的被控对象输出保持在或接近指定的参考值。MPC 控制器使用以下标量性能指标进行输出参考跟踪：

$J_{y}(z k)=\sum_{{j}=1}^{n_{y}}\ \sum_{{i}=1}^p\left\{\frac{w_{{i},{j}}^{y}}{s_{{j}}^{y}}[r_{{j}}(k+i\vert k)-y_{{j}}(k+i\vert k)]\right\}^{{2}}.$

此处

k - 当前控制间隔。
p - 预测范围（区间数）。
ny - 被控对象输出变量的个数。
zk - QP 决策，取值为

$z_k^T=\left[u(k|k)^{T}\quad u(k+1|k)^{T}\ \ldots\ \ u(k+p-1|k)^{T}\quad\it\epsilon_{k}\right].$

yj(k+i|k) - 第 j 个被控对象在第 i 个预测水平步的输出预测值，单位为工程单位。
rj(k+i|k) - 第 j 个被控对象在第 i 个预测水平步的输出参考值，单位为工程单位。
$s_{{j}}^{y}$ - 第 j 个被控对象产量的比例因子，单位为工程单位。
$w_{{i},{j}}^{y}$ - 第 i 个预测水平步的第 j 个被控对象输出的调整权重（无量纲）。

值 ny、p、 $s_{{j}}^{y}$ 和 $w_{{i},{j}}^{y}$ 是恒定的控制器规格。控制器接收整个预测范围内的参考值 rj(k+i|k)。控制器使用状态观测器来预测被控对象的输出 yj(k+i|k)，这些输出取决于受控变量调整 (zk)、测量干扰 (MD) 和状态估计值。在间隔 k 时，可获得控制器状态估计值和 MD 值。因此，Jy 仅是 zk 的函数。

1.2 操纵变量跟踪

在某些应用中，例如当被控对象的输出多于操纵变量时，控制器必须将选定的操纵变量 (MV) 保持在或接近指定的目标值。MPC 控制器使用以下标量性能指标进行操纵变量跟踪：

$J_{u}(z k)=\sum_{j=1}^{n_{u}}\sum_{i=0}^{p-1}\left\{\frac{w_{i,j}^{u}}{s_{j}^{u}}[u_{j}(k+i\vert k)-u_{j,l a r g e t}(k+i\vert k)]\right\}^{2}.$

此处

k - 当前控制间隔。
p - 预测范围（区间数）。
nu - 受控变量的数量。
zk - QP 决策，取值为
uj,target(k+i|k) - 第 j 个 MV 在第 i 个预测水平步的目标值，单位为工程单位。
$s_{{j}}^{u}$ - 第 j 个 MV 的比例因子，单位为工程单位。
$w_{{i},{j}}^{u}$ - 第 j 个 MV 在第 i 个预测水平步的调整权重（无量纲）。

数值 nu、p、 $s_{{j}}^{u}$ 和 $w_{{i},{j}}^{u}$ 是恒定的控制器规格。控制器接收整个范围内的 uj,target(k+i|k) 值。控制器利用状态观测器预测被控对象的输出。因此，Ju 只是 zk 的函数。

1.3 操纵变量移动抑制

大多数应用都喜欢小的 MV 调整（移动）。MPC 常量使用以下标量性能指标来抑制操纵变量移动：

$J_{\Delta u}(z_{k})=\sum_{j=1}^{n_{u}}\sum_{i=0}^{p-1}\left\{\frac{\displaystyle w_{i,j}^{\Delta u}}{\displaystyle s_{j}^{{u}}}[u_{j}(k+i\vert k)-u_{j}(k+i-1\vert k)]\right\}^{2}.$

此处

k - 当前控制间隔。
p - 预测范围（区间数）。
ny - 被控对象输出变量的个数。
zk - QP 决策，取值为

$z_k^T=\left[u(k|k)^{T}\quad u(k+1|k)^{T}\ \ldots\ \ u(k+p-1|k)^{T}\quad\it\epsilon_{k}\right].$

$s_{{j}}^{u}$ - 第 j 个 MV 的比例因子，单位为工程单位。
$w_{i,j}^{\Delta u}$ - 第 j 个 MV 运动在第 i 个预测水平步的调整权重（无量纲）。

$n_{u},\,p_{,}\,\,s_{j}^{u},w_{i,j}^{\Delta u}$ 的值是控制器的常数。u(k-1|k) = u(k-1)，是上一个控制区间的已知 MV。JΔu 仅是 zk 的函数。

此外，控制区间 m < p（或 MV 阻塞）会限制某些 MV 移动为零。

1.4 违反约束

在实践中，违反约束可能是不可避免的。软约束允许在这种情况下获得可行的 QP 解决方案。MPC 控制器采用一个无量纲、非负的松弛变量 εk，它量化了最坏情况下的约束违规。(见约束条件）相应的性能指标为

$J_{\varepsilon}(z k)=\rho_{\varepsilon}\varepsilon_{k}^{2}.$

这里

zk - QP 决策，取值为

$z_{k}^{T}=\bigl[u(k|k)^{T}\ \ \ u(k+1|k)^{T}\ \ \ldots\ \ u(k+p-1|k)^{T}\ \ \epsilon_{k}\bigr].$

εk - 控制区间 k 的松弛变量（无量纲）。

ρε - 违反约束条件的惩罚权重（无量纲）。

二、替代成本函数

您可以选择使用以下替代标准成本函数的方法：

$J(z_{k})=\sum_{i=0}^{p-1}\left\{\left[e_{y}^{T}(k+i)Q e_{y}(k+i)\right]+\left[e_{u}^{T}(k+i)R_{u}e_{u}(k+i)\right]+\left[\Delta u^{T}(k+i)R_{\Delta u}\Delta u(k+i)\right]\right\}+\rho_{\epsilon}\varepsilon_{k}^{2}.$

这里，Q（ny-by-ny）、Ru 和 RΔu（nu-by-nu）是正半无穷权重矩阵，并且：

$\begin{array}{c}{{e_{y}(i+k)=S_{y}^{-1}[r(k+i+1|k)-y(k+i+1|k)]}}\\ {{e_{u}(i+k)=S_{u}^{-1}[u_{t a r g e t}(k+i|k)-u(k+i|k)]}}\\ {{\Delta u(k+i)=S_{u}^{-1}[u(k+i]k)-u(k+i-1|k)].}}\end{array}$

也是、

Sy - 被控对象输出可变比例系数的对角矩阵，单位为工程单位。

Su - 以工程单位表示的 MV 比例因子对角矩阵。

r(k+1|k) - 第 i 个预测水平步的 ny 个被控对象输出参考值，单位为工程单位。

y(k+1|k) - 第 i 个预测水平步的 ny 个被控对象的工厂产出，单位为工程单位。

zk - QP 决策，取值为

$z_{k}^{T}=\bigl[u(k|k)^{T}\ \ \ u(k+1|k)^{T}\ \ \ldots\ \ u(k+p-1|k)^{T}\ \ \epsilon_{k}\bigr].$

utarget(k+i|k) - u(k+i|k) 对应的 nu MV 目标值，单位为工程单位。

与标准成本函数一样，输出预测使用状态观测器。

替代成本函数允许非对角线加权，但要求每个预测水平步的权重相同。

如果满足以下条件，替代成本函数和标准成本函数是相同的：

标准成本函数采用的权重 w , 和 w 相对于指数 i = 1:p 是常数。
矩阵 Q、Ru 和 RΔu 是对角线，对角元素是这些权重的平方。

三、约束条件

某些约束条件是隐含的。例如，控制范围 m < p（或 MV 阻塞）会强制某些 MV 增量为零，而用于被控对象输出预测的状态观测器是一组隐式相等约束。您可以配置的显式约束如下所述。

3.1 被控对象输出、MV 和 MV 增量的界限

最常见的 MPC 约束是边界，如下所示。

$\frac{y j,m i n(i)}{s_{j}^{y}}-\epsilon_{k}V_{j,m i n}^{y}(i)\leq\frac{y j(k+i| k)}{s_{j}^{y}}\leq\frac{y j,m a x(i)}{s_{j}^{y}}+\epsilon_{k}V_{j,m a x}^{y}(i),\qquad i=1:p,\qquad j=1:n_{y}$

$\frac{u j,m i n(i)}{s_{j}^{u}}-\epsilon k V_{j,m i n}^{u}(i)\leq\frac{u j(k+i-1|k)}{s_{j}^{u}}\leq\frac{u j,m a x(i)}{s_{j}^{u}}+\epsilon k V_{j,m a x}^{u}(i),\quad i=1:p,\quad\quad j=1:n u\quad$

$\frac{\Delta u_{j,m i n}(i)}{s_{j}^{u}}-\epsilon k V_{j,m i n}^{\Delta u}(i)\leq\frac{\Delta u_{j}(k+i-1|k)}{s_{j}^{u}}\leq\frac{\Delta u_{j,m a x}(i)}{s_{j}^{u}}+\epsilon k V_{j,m a x}^{\Delta u}(i),\quad i=1:p,\quad\quad j=1:n u,$

这里的 V 参数（ECR 值）是无量纲控制器常数，类似于成本函数权重，但用于约束软化（参见约束软化）。此外还有

εk - 用于约束软化的标量 QP 松弛变量（无量纲）。

syj - 第 j 个被控对象输出的比例因子，单位为工程单位。

suj - 第 j 个 MV 的比例因子，单位为工程单位。

yj,min(i)、yj,max(i) - 第 j 个被控对象在第 i 个预测水平步的产量下限和上限，单位为工程单位。

uj,min(i)、uj,max(i) - 第 j 个 MV 在第 i 个预测水平步的下限和上限，单位为工程单位。

Δuj,min(i)、Δuj,max(i) - 第 i 个预测水平步的第 j 个 MV 增量的下限和上限，单位为工程单位。

除松弛变量非负条件外，上述所有约束条件都是可选的，默认为非活动状态（即初始化为无限极限值）。要包含约束条件，必须在设计控制器时指定有限极限值。

四、QP 矩阵

本节介绍与优化问题中描述的模型预测控制优化问题相关的矩阵。

4.1 预测

假设输入干扰模型中描述的干扰模型为单位增益，即 d(k) = nd(k) 为白高斯噪声。可以将此问题表示为

${x\leftarrow \begin{bmatrix} x\\ x_d \end{bmatrix},A\leftarrow \begin{bmatrix} A & B_d\bar{C} \\ 0 & \bar{A} \end{bmatrix},B_u\leftarrow \begin{bmatrix}B_u\\ 0\end{bmatrix},B_v\leftarrow \begin{bmatrix}B_v\\ 0\end{bmatrix},B_d \leftarrow \begin{bmatrix}B_d\bar{D}\\ \bar{B}\end{bmatrix},C\leftarrow \begin{bmatrix} C & D_d\bar{C} \end{bmatrix}}$

那么，预测模型就是

$x(k+1)=A x(k)+B_{u}u(k)+B_{\nu}\nu(k)+B_{d}n_{d}(k)$

$y(k)=C x(k)+D_{\nu}\nu(k)+D_{d}n_{d}(k)$

接下来，考虑预测模型在时间 k=0 时的未来轨迹问题。对所有预测时刻 i 设置 nd(i)=0，得到

$y(i|0)=C\left[A^{i}x(0)+\sum_{h=0}^{i-1}A^{i-1}\left(B_{u}\left({{u(-1)+\sum_{j=0}^{h}}{\Delta u(j)}}\right)+B_{\nu}v(h)\right)\right]+D_{\nu}v(i)$

该方程给出的解是

$\left[\begin{array}{l}{{y(1)}}\\ {{\cdots}}\\ {{y(p)}}\end{array}\right]=S_{x}x(0)+S_{u1}u(-1)+S_{u}\left[\begin{array}{c}{{\Delta u(0)}}\\ {{\cdots}}\\ {{\Delta u(p-1)}}\end{array}\right]+H_{v}\left[\begin{array}{l}{{\nu(0)}}\\ {{\cdots}}\\ {{\nu(p)}}\end{array}\right]$

其中

$S_{x}=\left(\begin{array}{l}{{C A}}\\ {{C A^{2}}}\\ {{\dots}}\\ {{C A^{p}}}\end{array}\right)\left.\in\mathfrak{R}^{p n_{y}\times n_{x}},S_{u1}=\left[\begin{array}{l}{{C B_{u}}}\\ {{C B_{u}+C A B_{u}}}\\ {{\dots}}\\ {{\sum_{h=0}^{p-1}C A^{h}B_{u}}}\end{array}\right]\right.\in\mathfrak{R}^{p n_{y}\times n_{u}}$

$S_{u}=\begin{bmatrix} {C B_{u}} & 0 & \cdots & 0 \\ {C B_{u}+C A B_{u}} & {C B_{u}} & \cdots & 0 \\ \cdots&\cdots & \cdots&\cdots \\\sum_{h=0}^{p-1}C A^{h}B_{u} & \sum_{h=0}^{p-2}C A^{h}B_{u}&\cdots &{C B_{u}} \end{bmatrix}\in\mathfrak{R}^{p n_{y}\times n_{u}}$

${H_{v}=\begin{bmatrix} {C B_{v}} & D_v & 0 & \cdots & 0 \\ {CA B_{v}} & {C B_{v}} &D_v& \cdots & 0 \\ \cdots&\cdots & \cdots&\cdots&\cdots \\\sum_{h=0}^{p-1}C A^{h}B_{v} & \sum_{h=0}^{p-2}C A^{h}B_{v}&\sum_{h=0}^{p-3}C A^{h}B_{v}&\cdots &{D_v} \end{bmatrix}\in\mathfrak{R}^{p n_{y}\times (p+1)n}}$

4.2 优化变量

设 m 为自由控制移动的次数，设 z= [z0; ...; zm-1]。那么

$\left[\begin{array}{c}{{\Delta u(0)}}\\ {{\ldots}}\\ {{\Delta u(p-1)}}\end{array}\right]=J M\left[\begin{array}{c}{{z0}}\\ {{z m-1}}\end{array}\right]$

其中，JM 取决于阻塞动作的选择。z0、......、zm-1 与松弛变量ɛ 一起构成了优化问题的自由优化变量。在系统只有一个操纵变量的情况下，z0、......、zm-1 是标量。

考虑下图中描述的阻塞动作。

阻塞移动：移动 = [2 3 2] 的输入和输入增量

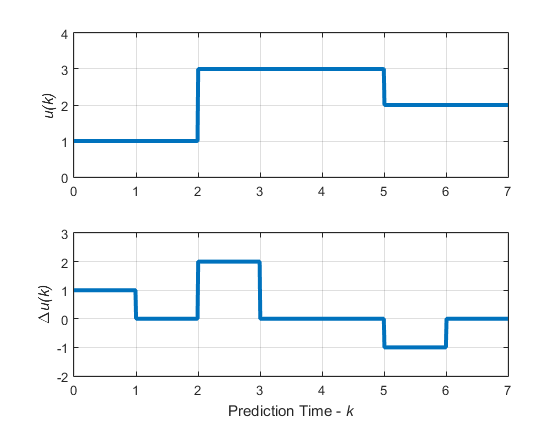
这个图形对应于选择 moves=[2 3 2]，或者等价于 u(0)=u(1)，u(2)=u(3)=u(4)，u(5)=u(6)，Δ u(0)=z0，Δ u(2)=z1，Δ u(5)=z2，Δ u(1)=Δ u(3)=Δ u(4)=Δ u(6)=0.

那么，相应的矩阵 JM 为

$J_M=\begin{array}{r}{\left[{\begin{array}{r r r}{I}&{0}&{0}\\ {0}&{0}&{0}\\ {0}&{I}&{0}\\ {0}&{0}&{0}\\ {0}&{0}&{0}\\ {0}&{0}&{I}\\ {0}&{0}&{0}\end{array}}\right]}\end{array}$

有关操纵变量阻塞的更多信息，请参阅操纵变量阻塞。

4.3 成本函数

标准形式。要优化的函数是

$J(z,\varepsilon)=\left ({\begin{bmatrix}u(0)\\ \dots\\ u(p-1)\end{bmatrix} } - {\begin{bmatrix}u_{target}(0)\\ \dots\\ u_{target}(p-1)\end{bmatrix} }\right )^T W_u^2 \left ({\begin{bmatrix}u(0)\\ \dots\\ u(p-1)\end{bmatrix} } - {\begin{bmatrix}u_{target}(0)\\ \dots\\ u_{target}(p-1)\end{bmatrix} }\right ) + {\begin{bmatrix}\Delta u(0)\\ \dots\\ \Delta u(p-1)\end{bmatrix}^T { W}_{\Delta u}^{2} {\begin{bmatrix}\Delta u(0)\\ \dots\\ \Delta u(p-1)\end{bmatrix}} }$

${+ \left ({\begin{bmatrix}y(1)\\ \dots\\ y(p)\end{bmatrix} }-{\begin{bmatrix}r(1)\\ \dots\\ r(p)\end{bmatrix} } \right )^T{ W}_{y}^{2} \left ({\begin{bmatrix}y(1)\\ \dots\\ y(p)\end{bmatrix} }-{\begin{bmatrix}r(1)\\ \dots\\ r(p)\end{bmatrix} } \right ) + \rho_{\mathcal{E}}{\mathcal{E}}^{2}}$

其中

$W_{u}=\mathrm{diag}\!\left({w}_{0,1}^{u},{w}_{0,2}^{u},...,{w}_{0,n}^{u},...,{w}_{p-1,1}^{u}\!,{w}_{p-1,2}^{u}\!,{w}_{p-1,2}^{u}\!,\dots,{w}_{p-1,n}^{u}\!\right)$

$W\Delta u=\mathrm{diag}\biggl(w_{0,1}^{\Delta u},w_{0,2}^{\Delta u},...,w_{0,n_{u}}^{\Delta u},...,w_{p-1,1}^{\Delta u},w_{p}^{\Delta u},...,w_{p-1,n_{u}}^{\Delta u}\biggr)$

$W_{y}=\mathrm{diag}\!\left(w_{1,1}^{y},w_{1,2}^{y}\!\cdot\!...,w_{1,n_{y}}^{y},...,w_{p,1}^{y},w_{p,2}^{y}\!....,w_{p,n_{y}}^{y}\right)$

最后，在代入 u(k)、Δu(k)、y(k)之后，J(z) 可重写为

$J(z,\varepsilon)=\rho_{\mathcal{E}}\varepsilon^{2}+z^{T}K\Delta u z+ 2\left ( {\begin{bmatrix}r(1)\\ \dots\\ r(p)\end{bmatrix} }^T K_r + {\begin{bmatrix}v(0)\\ \dots\\ v(p)\end{bmatrix} }^T K_v + u(-1)^{T}K_u + {\begin{bmatrix}u_{target}(0)\\ \dots\\ u_{target}(p-1)\end{bmatrix} }^T K_{ut} + +\;x(0)^{T}K x\right )z+{C}_{y}W_{y} c {y}++{C}_{u}W_{u} c {u}$ 其中

$c_{y}=S_{X}x(0)+S_{u}1u(-1)+H_{v}\left[\begin{array}{l}{{v(1)}}\\ {{\cdots}}\\ {{v(p)}}\end{array}\right]-\left[\begin{array}{l}{{r(1)}}\\ {{\cdots}}\\ {{r(p)}}\end{array}\right]$

注意事项

您可能希望 QP 问题保持严格的凸性。如果 Hessian 矩阵 KΔU 的条件数大于 1012，请在每个对角项上添加 10*sqrt(eps)。只有当所有输入率都未受惩罚（WΔu=0）时，才能使用此解决方案（请参阅 mpc 对象的权重属性）。

替代成本函数。如果使用 "替代成本函数 "中所示的替代成本函数，则等式 1 由以下公式代替：

$\begin{array}{l}{{W_{u}={\mathrm{blkdiag}}(R_{u},\ldots,R_{u})}}\\ {{W_{\Delta u}={\mathrm{blkdiag}}(R_{\Delta u,\ldots,R_{\Delta u})}}}\\ {{W_{y}={\mathrm{blkdiag}}(Q,\ldots,Q)}}\end{array}$

在这种情况下，分块对角矩阵重复 p 次，例如，预测范围内每一步重复一次。

您也可以选择使用标准形式和替代形式的组合。更多信息，请参阅 mpc 对象的权重属性。

约束条件接下来，考虑输入、输入增量和输出的限制以及约束条件 ɛ≥ 0。

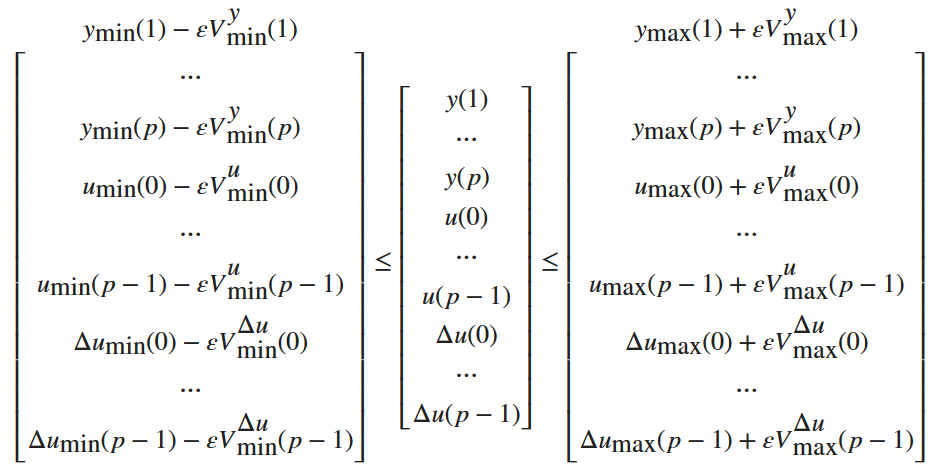
注释

为减少计算量，控制器会自动消除无关的约束条件，如无限边界。因此，实时使用的约束集可能远小于本节建议的约束集。

与计算成本函数类似，可以将 u(k)、Δu(k)、y(k) 代入，得到

这篇关于MATLAB - MPC - 优化问题（Optimization Problem）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

MATLAB - MPC - 优化问题（Optimization Problem）

系列文章目录

前言