数字逻辑电路入门：从晶体管到逻辑门

本文主要是介绍数字逻辑电路入门：从晶体管到逻辑门，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

数字逻辑电路入门：从晶体管到逻辑门

这是数字逻辑电路中最基础的部分。但是并非那么容易理解。

1、晶体管

1. mosfet：场效应晶体管，是电压控制元件。
2. cmos：是指由mos管构成的门级电路通常是互补的。
3. BJT：一种三极管，是电流控制元件，用来放大电流，功耗大于mos管。
4. nmos：衬底是p型半导体，源极和漏极是n型掺杂区域。适合用来导通低电压，不适合导通高电压。
5. pmos：和nmos相反，衬底是n型半导体，源极和漏极是p型掺杂区域。适合用来导通高电压，不适合导通低电压。
6. pmos用在上拉网络，nmos用在下拉网络。

2、逻辑门

互补传导规则：nmos串联，pmos必须并联；nmos并联，pmos必须串联。保证上拉网络和下拉网络不会同时导通，即不出现短路。

1. 非门：输入a，输出y，消耗2个晶体管
   1. 一个pmos，栅极接a，源极接vcc，漏极接y
   2. 一个nmos，栅极接a，源级接y，漏极接gnd
   3. 分析，a=1，mos的栅极上表面聚集正电荷，下表面聚集负电荷。pmos衬底是n型半导体，本身有自由电子，因此源极和漏极仍然断开。nmos衬底是p型半导体，本身有自由空穴，聚集负电荷之后，源极和漏极接通，因此y=0。
2. 与门：消耗6个晶体管
   1. 一个与非门
   2. 级联一个非门
3. 或门：消耗6个晶体管
   1. 一个或非门
   2. 级联一个非门
4. 或非门：消耗4个晶体管
   1. 两个pmos串联，栅极接a，b，源极接vcc，漏极接y
   2. 两个nmos并联，栅极接a，b，源极接vcc，漏极接y
   3. 分析，a=0，b=0，pmos均导通，nmos均断开，y=1；a、b有一个为1，下拉网络导通，上拉网络断开，y=0
5. 与非门：消耗4个晶体管
   1. 两个pmos并联，栅极接a，b，源极接vcc，漏极接y
   2. 两个nmos串联，栅极接a，b，源极接vcc，漏极接y
   3. 分析，a=1，b=1，pmos均断开，nmos均导通，y=0；a、b有一个为0，下拉网络断开，上拉网络导通，y=1
6. 异或门：
   1. 实现方式两种，一个使用10个晶体管，一个使用12个晶体管
   2. 参考：COMS门电路的设计及其优化–以异或门为例
7. 同或门
8. 三态门

3、卡诺图化简

以下图为例：

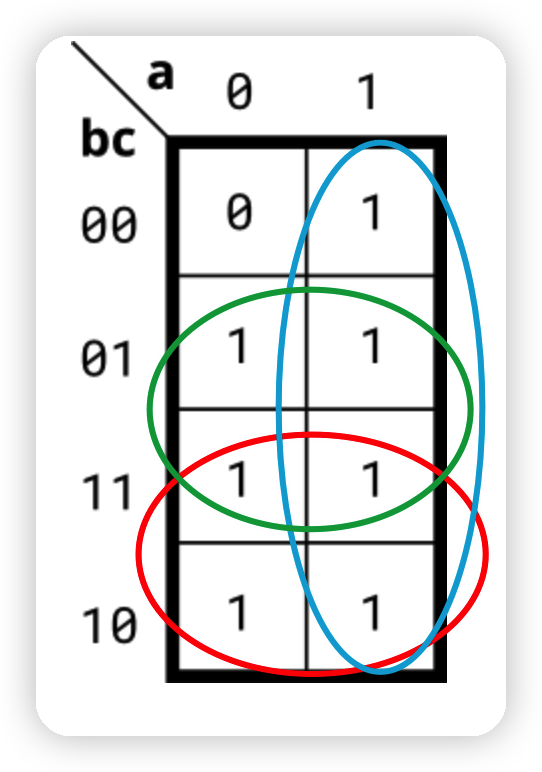
1. 画出卡诺图，注意格雷码序；
2. 画圈：
   1. 从大到小画圈，16格、8格、4格、2格、1格；
   2. 每个圈都要圈住1，最终圈住所有1；
   3. 可环绕画圈。
3. 写出SOP（sum-of-products）
   1. 每个圈代表一个product，读法是“相异相消”；
   2. 将所有product相加；
   3. Y = b+c+a;（按照红、绿、蓝的顺序写的product）
4. 补充：“相异相消”
   1. 比如$Y=AB+A\bar{B}=A(B+\bar{B})=A$；
   2. $B+\bar{B}=1$恒成立；
   3. 圈中变量相异的，则无需管，相同的如实记录。
   4. 比如红圈，c相异，a相异，b相同且为1，则记录为b。

另一个例子：

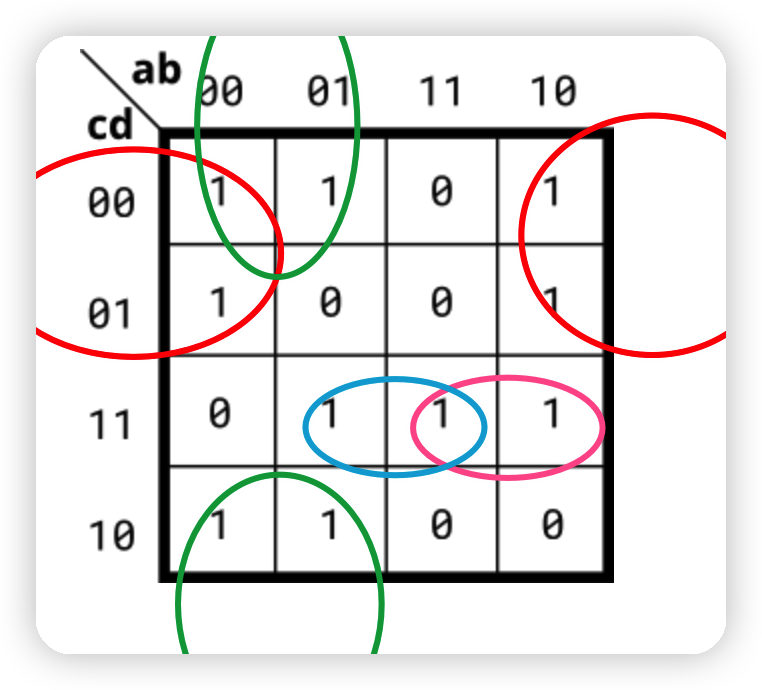
1. 画圈
2. 读SOP
   1. 红：$\bar{b}\bar{c}$
   2. 绿：$\bar{a}\bar{d}$
   3. 粉：$acd$
   4. 蓝：$bcd$
   5. $Y=\bar{b}\bar{c}+\bar{a}\bar{d}+acd+bcd$

可以想到：

1. 圈1则是SOP
2. 圈0则是POS
3. 因此，谁少圈谁。
4. 注意，圈0写出POS之后取反，利用布尔代数则得到圈0的POS。

4、复用器

使用逻辑门可以搭建一个复用器

1. $Y=D_0\bar{S}+D_{1}S$
2. 两个与门、一个非门、一个或门
3. 优化：减少晶体管，$Y=D_0\bar{S}+D_{1}S=({\bar{D}}_0+S)\overline{(D_{1}S)}$
4. 一个与非门、一个与门、一个或门、一个非门

这篇关于数字逻辑电路入门：从晶体管到逻辑门的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---