本文主要是介绍运筹说 第82期 | 算法介绍之图与网络分析(二),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

本期我们继续进行运筹学之图与网络分析算法的讲解,我们将对图与网络分析的基础知识进行一个简单的回顾,并介绍求解最大流问题和最小费用最大流的MATLAB和Python相关代码,以帮助大家利用工具快速求解最大流问题和最小费用最大流问题,做到事半功倍。由于篇幅有限,小编接下来只展示部分代码,小伙伴们可以关注“运筹说”公众号→后台回复“算法介绍之图与网络分析(二)”获取完整代码。话不多说,我们一起来看看吧!
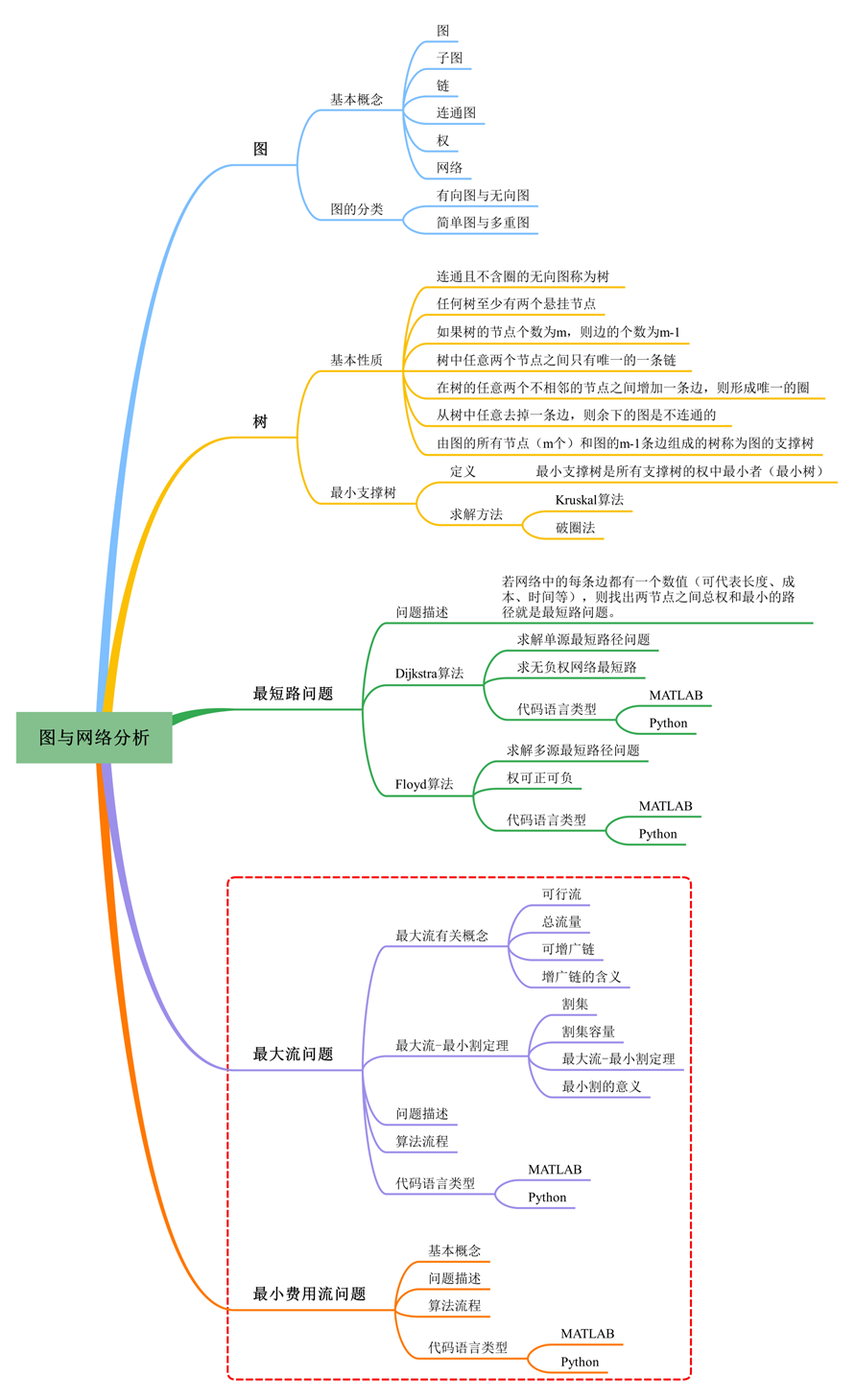 一、基础知识
一、基础知识
1、最大流问题
★ 最大流有关概念
(1) 可行流:对任一G中的边(vi, vj)有流量fij,称集合f={fij}为网络G上的一个流。且称满足容量限制条件和平衡条件的流f为可行流。
①容量限制条件:对G中每条边(vi, vj),有0≤fij≤cij;
②平衡条件:对中间点vi有∑j fij =∑k fki,即物资的输入量与输出量相等。
(2)总流量:对收、发点vt,vs,有∑i fsi =∑j fjt=W,W为网络流的总流量。
(3)可增广链:容量网络G,若μ为网络中从vs,vt的一条链,给μ定向为从vs到vt,μ上的边凡与μ同向称为前向边,凡与μ反向称为后向边,其集合分别用μ+和μ-表示,f是一个可行流,如果满足
则称μ为从vs到vt的(关于f的)可增广链。
(4) 可增广链的意义:沿着这条链从发点到收点输送的流,还有潜力可挖。
★ 最大流-最小割定理
(1) 割集:容量网络G=(V,E,C),vs,vt为发、收点,若有边集E’为E的子集,将G分为两个子图G1,G2,其顶点集合分别记S,S’,S∪S’=V,S∩S’=∅,vs,vt分属S,S’,满足:①G(V,E- E’)不连通;②E’’为E’的真子集,而G(V,E- E’’)仍连通,则称E为G的割集,记E’=(S,S’)。
(2) 割集容量:割集(S,S’)中所有始点在S,终点在S’的边的容量之和,称为(S,S’)的割集容量,记为C(S,S’)。容量网络G的割集有多个,其中割集容量最小者称为网络G的最小割集容量(简称最小割)。
(3) 最大流-最小割定理:任一个网络G中,从vs到vt的最大流的流量等于分离vs、vt的最小割的容量。
(4) 最小割的意义:网络从发点到收点的各通路中,由容量决定其通过能力,最小割则是这些路中的咽喉部分,其容量最小,它决定了整个网络的最大通过能力。要提高整个网络的运输能力,必须首先改造这个咽喉部分的通过能力。
★ 问题描述
求网络中一个可行流,使其流量达到最大,这种流称为最大流,这个问题称为(网络)最大流问题。
★ 算法流程

2、最小费用流问题
★ 基本概念
(1) 链的费用:已知网络G=(V,E,C,d),f是G上的一个可行流,μ为从vs到vt的(关于f的)可增广链,则链μ的费用为
若μ*是从vs到vt所有可增广链中费用最小的链,则称μ*为最小费用可增广链。
(2) 长度网络:对网络G=(V,E,C,d),有可行流f,保持原网络各点,每条边用两条方向相反的有向边代替,各边的权lij按如下规则:
①当边(vi, vj)∈E,令

这里+∞的意义是:这条边已饱和,不能再增大流量,否则要花费很高的代价,实际无法实现,因此权为+∞的边可从网络中去掉。
②当边(vj, vi)为原来G中边(vi, vj)的反向边,令

这里+∞的意义是此边流量已减少到0,不能再减少,权为+∞的边也可以去掉。
这样得到的网络L(f)称为长度网络(将费用看成长度)。
★ 问题描述
已知容量网络G=(V,E,C),每条边(vi, vj)除了已给出容量cij外,还给出了单位流量的费用dij(≥0),记G=(V,E,C,d)。求G的一个可行流f={fij},使得流量W( f )=v,且总费用最小。
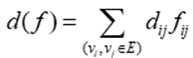
特别地,当要求f为最大流时,此问题即为最小费用最大流问题。
★ 算法流程

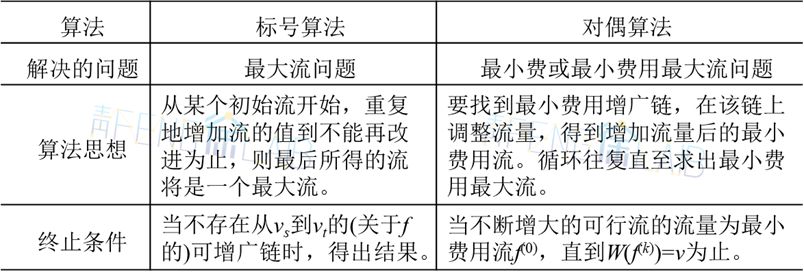
3、算法对比
二、算法实现
1、最大流问题
(1)例题介绍
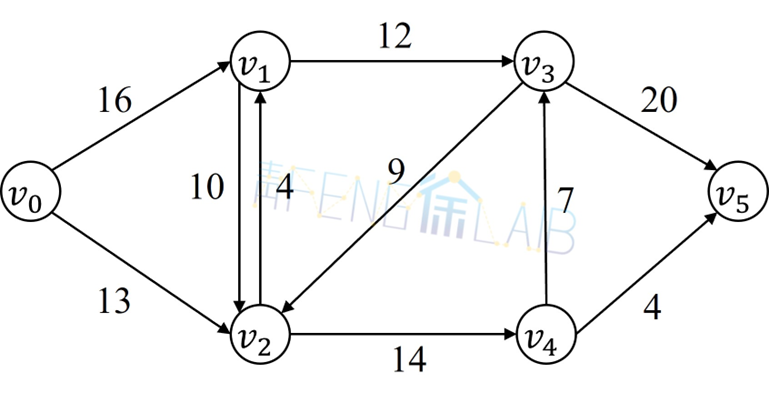
给定指定的一个有向图,v0为起点,v5为起点,每条边有指定的容量,求满足条件的从v0到v5的最大流。
(2)平台实现
我们以上述例题为例,借助MATLAB和Python介绍实现求解最大流问题的相关代码。
①MATLAB
★ 代码展示


★ 代码调用
代码运行及最终结果展示如下,求得v0到v5的最大流为23,其中v0流向v1的流量为11,v0流向v2的流量为12,v2流向到v1的流量为1,v1流向到v3的流量为12,v2流向到v4的流量为11,v4流向v3的流量为7,v3流向v5的流量为19,v4流向v5的流量为4。

②Python
★ 代码展示

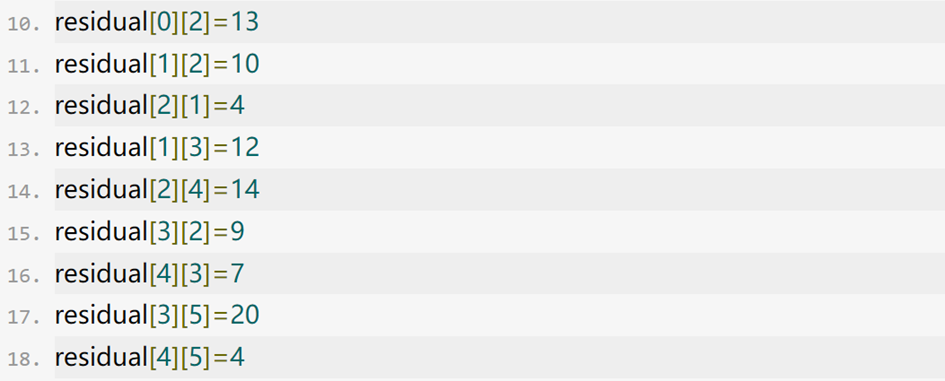
★ 代码调用
代码运行及最终结果展示如下,求得v0到v5的最大流为23,其中v0流向v1的流量为11,v0流向v2的流量为12,v2流向到v1的流量为1,v1流向到v3的流量为12,v2流向到v4的流量为11,v4流向v3的流量为7,v3流向v5的流量为19,v4流向v5的流量为4。

(3)图形结果展示
v0到v5的最大流为23,每条边的流向及流量如图所示。

2、最小费用流问题
(1)例题介绍
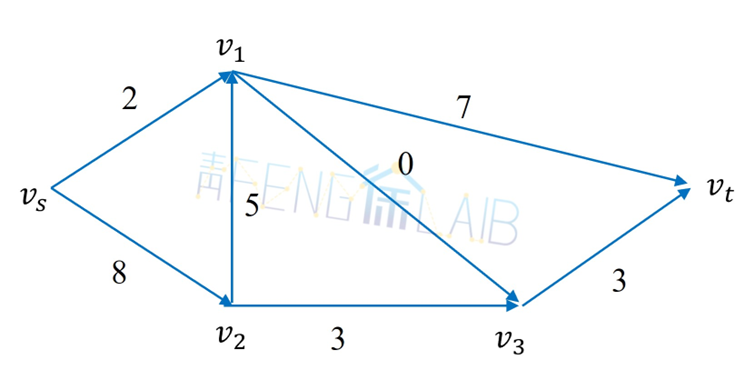
在如图所示的运输网络上,求流量v为10的最小费用流,边上括号内为(cij, dij)。

(2)平台实现
我们以上述例题为例,借助MATLAB和Python介绍实现求解最小费用流问题的相关代码。
①MATLAB
★ 代码展示

 ★ 代码调用
★ 代码调用
代码运行及最终结果展示如下,本例中MATLAB代码以1代表起点vs,以5代表终点vt,求得流v为10的最小费用流为48,其中vs到v1的流量为4,vs到v2的流量为8,v2到v1的流量为5,v2到v3的流量为3,v1到v3的流量为0,v3到vt的流量为3,v1到vt的流量为7。

②Python
★ 代码展示


★ 代码调用
代码运行及最终结果展示如下,本例中Python代码以0代表起点vs,以4代表终点vt,求得流量v为10的最小费用流为48,其中vs到v1的流量为4,vs到v2的流量为8,v2到v1的流量为5,v2到v3的流量为3,v1到v3的流量为0,v3到vt的流量为3,v1到vt的流量为7。

(3)图形结果展示
流量为10时vs到vt的最小费用流为48,每条边的流向及流量如图所示。
三、参考资料
【最大流问题Python实现】
https://blog.csdn.net/anlian523/article/details/81202622
【最小费用流问题Python实现】
https://zhuanlan.zhihu.com/p/103521228
本期的内容就介绍到这里,想要进一步了解运筹学,关注本公众号,快快学起来吧!
作者 | 尹萌娟 王连聚
责编 | 刘文志
审核 | 徐小峰
这篇关于运筹说 第82期 | 算法介绍之图与网络分析(二)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





