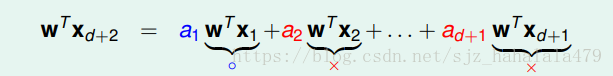【林轩田】机器学习基石（七）——VC维

本文主要是介绍【林轩田】机器学习基石（七）——VC维，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Lecture 7: VC Dimension VC维

ppt
video

7.1 Definition of VC Dimension VC维的定义

复习1

上节课，林教授讲到了，当样本$N$足够大，且成长函数$m_{H}(N)$存在断点$k$时，可以概率性地推出$E_{out} \simeq E_{in}$

即

$$有断点k的m_{H}(N) \le B(N,k) \le \sum_{i=0}^{k-1}\dbinom{N}{i}[最大为N^{k-1}]$$

复习2 VC边界

对演算法$A$在数据空间$D$上选择的任何假设$g$，当$D$在统计学意义上足够大时，这个假设是坏假设的几率是

$$P_{D}[|E_{out}(g)-E_{in}(g)| > \epsilon] \\ \le P_{D}[ \exists h \in H, s.t. |E_{out}(g)-E_{in}(g)| > \epsilon] \\ \le 4m_{H}(2N)exp(-\frac{1}{8}\epsilon^{2}N) \\ \le 4*(2N)^{k-1}exp(-\frac{1}{8}\epsilon^{2}N) [如果k存在的话]$$

所以，如果

• $$m_{H}(N)有断点k，H是好的假设$$
• $$N足够大，D是好的数据集$$
  以上两点推出， $$E_{in} \simeq E_{out}$$
• 如果，演算法$A$选择了一个有小$E_{in}$的$g$ ，$A$是好的演算法

有了上面三条，再加上好运气，我们就学到了好的规律！！

vc维定义

• vc维是最大的非断点的正式名称
  

假设函数$H$的VC维，记为$d_{VC}(H)$，是使得成长函数$m_{H}(N)=2^N$最大的N，即

• 假设函数$H$可以shatter的最多的输入数量

• $d_{vc} = 最小的断点k-1$
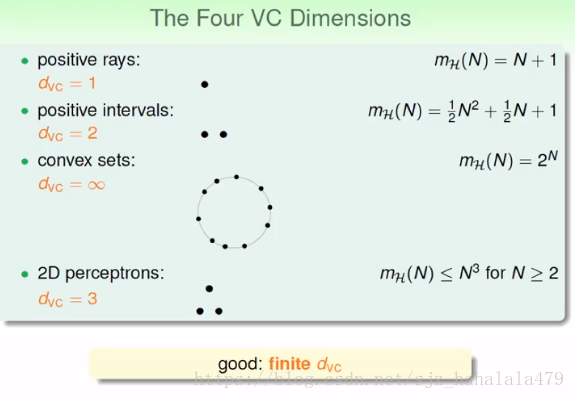
  如下图，这是上节课提出的几个例子：
  

• 所以，如果我们有有限个VC维的话，就可以推出不论选择哪个$g$，都能够保证$E_{in}(g) \simeq E_{out}(g)$，而不用关心

  • 演算法$A$长什么样。
  • 样本分布$P$长什么样。
  • 目标函数$f$长什么样。

7.2 VC dimension for perceptrons 感知器的VC维

矩阵相关

开始之前，我们先复习两个矩阵相关的概念。

逆矩阵

$设A为数域上的一个n阶方针，若在相同数域上存在另一个n阶方阵B，使得 AB = BA = E。$
$则称，B为A的逆矩阵，A为可逆矩阵。$
$注：E为单位矩阵。$

举个例子：

$$A = \left[ \begin{matrix} 1&2\\ 4&3 \end{matrix} \right]$$

求$A$的逆矩阵。
解：
假设

$$B = \left[ \begin{matrix} a&b\\ c&d \end{matrix} \right]$$

$$A*B = \left[ \begin{matrix} 1&2\\ 4&3 \end{matrix} \right] * \left[ \begin{matrix} a&b\\ c&d \end{matrix} \right] =\\ \left[ \begin{matrix} a+2c&b+2d\\ 4a+3c&4b+3d \end{matrix} \right] =\left[ \begin{matrix} 1&0\\ 0&1 \end{matrix} \right]$$
所以，
$$\left\{\begin{array}{lr}a+2c=1, & \\b+2d=0.\\4a+3c=0 \\4b+3d=1, & \end{array}\right.$$
得到,
$$B = \left[ \begin{matrix} -0.6&0.4\\ 0.8&-0.2 \end{matrix} \right]$$

线性相关

设$a_1,a_2,...a_m$为一组$n维向量$，若存在一组不全为0的实数$k_1,k_2,...k_m$，使得

$$k_1a_1+k_2a_2+k_3a_3+...+k_ma_m = 0$$
则称向量组$a_1,a_2,...,a_m$线性相关，反之，线性无关。

将向量组写成矩阵，如何通过矩阵的性质判断向量组是线性相关还是线性无关呢？

• 将矩阵进行初等行变换，化为阶梯型矩阵，若非零行的行数等于向量的个数，即矩阵满秩，则为向量组线性无关；若非零行行数小于向量个数，即矩阵非满秩，则向量组线性相关。

感知器的vc维

首先我们来回顾一下二维感知器：

在线性可分的情况下，PLA是可以找到最佳的$g$的，当迭代次数$T$足够大时，我们能保证$E_{in}(g) = 0$；
在之前关于机器学习可行性的论证中，二维线性分割问题的vc维等于3是有限的，在训练样本$N$足够大时，$E_{out}(g) \simeq E_{in}(g)$

所以，我们能推出，在二维线性可分问题中， PLA的$E_{out}(g) \simeq 0$。

现在，我们提出一个问题，PLA在多维情况下仍旧可行吗？

注意到一维的感知机$d_{vc}=2$，二维的感知机$d_{vc}=3$；
猜想，$D$维的感知机$d_{vc}=d+1$

如何验证这个猜想呢？分为两步：

1. 验证$d_{vc} \ge d+1$
2. 验证 $d_{vc} \le d+1$

首先证明$d_{vc} \ge d+1$，因为$vc$维的定义是，能够被shatter的最大输入数量；如果我们能找到至少1个$d$维的能shatter的最大输入数量是$d+1$的情形，那么就可以说$d_{vc} \ge d+1$

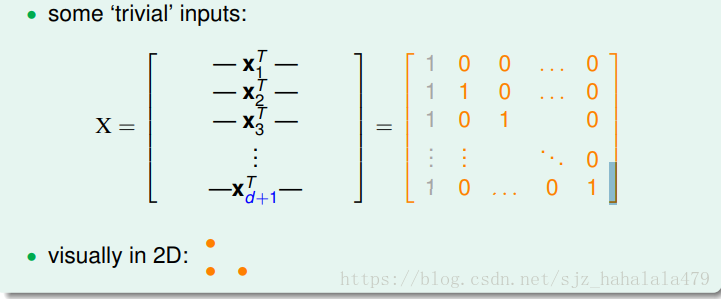
我们构造一个有$d+1$个inputs的$d$维矩阵：

$$X = \left[ \begin{matrix} 0&0&0&...&0\\ 1&0&0&...&0\\ 0&1&0&...&0\\ 0&0&1&...&0\\ ...\\ ...\\ 0&0&0&...&1\\ \end{matrix} \right]$$

第一个input向量代表原点，有d个0；其余d行向量分别代表某一维值为1，其它维值为0的向量。

注意到图中灰色的一列，我们给向量的左边添加一列常数1，代表threshold。

当$d = 1$时:

$$X = \left[ \begin{matrix} 0\\ 1 \end{matrix} \right]$$
可见$d+1=2$个inputs是shatter的
当$d=2$时：
$$X = \left[ \begin{matrix} 0&0\\ 1&0\\ 0&1\\ \end{matrix} \right]$$
也就是说在二维平面直角坐标系上，是(0,0),(1,0)和(0,1)三个点，我们在几何上可以很容易证明，这三个点是shatter的。

我们说$d+1$个inputs是shatter的，就是说假设空间中，包含输出$y$的全排列，就是对任意的$y$，

$$y=\left[ \begin{matrix} y_1\\ y_2\\ ...\\ y_{d+1}\\ \end{matrix} \right]$$
总能找到一个$w$，使得$sign(wX)=y$ 成立。

注意到我们构造的矩阵是可逆的，所以$wX = y \rightarrow w=X^{-1}y$总是成立的。

这里我们证明了第一个不等式，即我们找到了d维的d+1个inputs可以被shatter。

如何证明$d_{vc} <= d+1$呢？我们需要证明，对d维的任意$d+2$个输入来说，都是不能被shatter的。

考虑一个二维的例子，$d=2,d+2=4$,也就是4行2列的矩阵，我们在左边偷偷再加一列常数1表示threshold，这样就构成了一个4行3列的矩阵。

这四个点在平面直角坐标系上的表示，分别是(0,0)，(1,0),(0,1),(1,1)，根据以前的学习，我们知道这四个点是不能被shatter的。

也就是说，如果我们定好了另外三个点分别是圈、叉、圈，第四个点一定不能是叉，只能是圈，用线性代数表示：

$$w^Tx_4 = w^Tx_2 + w^Tx_3 - w^Tx_1 > 0$$

从矩阵的角度来说，如果一个矩阵的行数大于列数，这个矩阵的向量组是线性相关的。

这里假设，$a_n$与$w^Tx_n$的符号相同，也就是说，我们假设$a_1$是正的，$a_2,a_3....,a_{d+1}$是负的，那么

根据负负得正，$w^Tx_{d+2}$一定大于0；也就是说，不存在$x_{d+2}$为叉叉的情况，这样已经证明出，$d+2$个inputs是不能被shatter的，所以$d_{vc} <= d+1$

所以，我们证明了d维的感知机模型，$d_{vc} = d+1$。

7.3 Physical Intuition of VC Dimension vc维的直观物理解释

• 假设的参数$w$代表了自由程度(degrees of freedom)，参数越多，代表假设空间函数的可调节能力越强。
• 假设的数量，$M=|H|$，可以类比成自由程度。
• 上一小节提到的vc维，可以理解为有效地二元分割的自由程度。

• 根据经验，虽然不是总这样，$d_{vc}$的值和自由参数个数是相等的。

第五节课曾经讨论过$M$和机器学习两个核心问题的关系，将$M$转换为$d_{vc}$，结论类似。

• $d_{vc}$小时，坏事情发生的概率右边界小，也就是说我们有极高的概率保证$E_{out} \approx E_{in}$，但是同时因为$d_{vc}$较小，可以选择的$H$也少了，所以不能保证$E_{in}$足够小。
• 反之如是。

所以选择一个合适的$d_{vc}$，或者说合适的假设空间$H$,或者说合适的模型，是十分重要的。

Fun Time问题是，经过原点的也就是说固定$w_0$为0的感知器模型的$d_{vc}$是多少？这个问题可以从自有参数与$d_{vc}$的关系入手，因为自由参数少了一个，所以$d_{vc}$也相应地减1。答案是2，d。

7.4 Interpreting VC Dimension VC维的解释

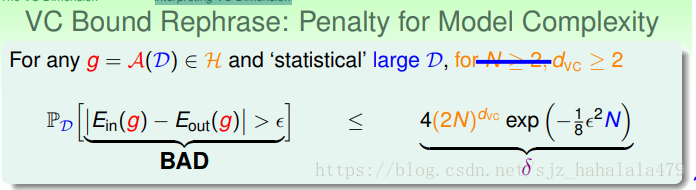
在深入解释vc维之前，我们先来回顾一下vc边界。vc边界指坏事发生的概率的右边界，用$\delta$表示。

换个说法，好事情发生概率的左边界就是$1-\delta$，即

$$P_{D}[|E_{in}(g) - E_{out}(g)| \le \epsilon] \ge 1- \delta$$
用$\delta$表示$\epsilon$，得到

也就是说，在$1-\delta$的概率下：

$$|E_{in}(g)-E_{out}(g)| \le \sqrt{\frac{8}{N}ln(\frac{4(2N)^{d_{vc}}}{\delta})}$$
去掉绝对值，

$$E_{in}(g)-\sqrt{\frac{8}{N}ln(\frac{4(2N)^{d_{vc}}}{\delta})} \le E_{out}(g) \le \\ E_{in}(g)+\sqrt{\frac{8}{N}ln(\frac{4(2N)^{d_{vc}}}{\delta})}$$

我们重点关注右边界，使用$\Omega(N,H,\delta)$表示根号项的一大串内容，视为模型复杂度的惩罚项。

左图横轴是$d_{vc}$，纵轴是Error。

• 随着$d_{vc}$的增大，$E_{in}$是减小的。可以这么理解，$d_{vc}$增大了，代表假设空间中可供选择的$g$变多了，也就更容易找到小的$E_{in}$。
• 根据公式，$d_{vc}$增大，模型复杂度也在增大。
• $E_{out}$根据前两个的走势，大致呈现山谷形。

给定一些参数，计算需要训练样本$N$的值，我们发现，理论上样本$N = 10000d_{vc}$，但是经验上，$N=10d_{vc}$就可以了。
所以说我们的vc bound是十分宽松的，那它为什么如此宽松呢？原因如图。

这篇关于【林轩田】机器学习基石（七）——VC维的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---