本文主要是介绍295. Find Median from Data Stream数据流中的中位数,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目描述
如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。
解答
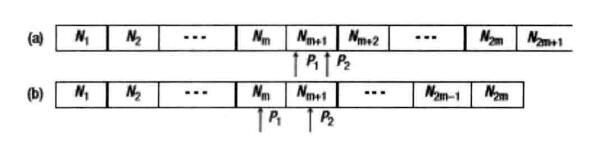
如上图所示,如果数据在容器中已经排序,那么中位数可以由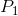
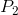
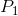
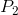
注意到,整个容器被分隔成了两部分。位于容器左边部分的数据比右边的数据小。另外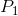
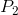
如果能够保证数据容器左边的数据都小于右边的数据,这样即使左右两边内部的数据没有排序,也可以根据左边最大的数和右边最小的数得到中位数。用最大推可以快速的从一个数据容器中找出最大数,最小堆可以快速的从一个数据容器中找出最小的数。
用一个最大堆实现左边的数据容器,用最小堆实现右边的数据容器。
首先,要保证数据平均分配到两个堆中。为了实现平均分配,可以在数据的总数目是偶数时把新数据插入到最小堆,否则插入到最大堆中。
还要保证最大堆中的数据都要小于最小堆中的数据。如果当前数据的总数目是偶数,也就是要插入最小堆,但是它比最大堆中的一些数还要小。此时,先将这个数插入到最大堆中,然后把最大堆中最大的数取出,插入到最小堆中。如果当前数据的总数目是奇数,也就是要插入最大堆,但是它比最小堆中的一些数还要大。此时,先将这个数插入到最小堆中,然后把最小堆中最小的数取出,插入到最大堆中。
基于STL中的函数push_heap(),pop_heap()来实现堆。使用仿函数less和greater分别用来实现最大堆和最小堆。
class Solution {
public:void Insert(int num){if(((min.size() + max.size()) & 0x1) == 0){if(!max.empty() && num<max[0]){max.push_back(num);push_heap(max.begin(),max.end(),less<int>());num = max[0];pop_heap(max.begin(),max.end(),less<int>());max.pop_back();}min.push_back(num);push_heap(min.begin(),min.end(),greater<int>());}else{if(!min.empty() && num>min[0]){min.push_back(num);push_heap(min.begin(),min.end(),greater<int>());num = min[0];pop_heap(min.begin(),min.end(),greater<int>());min.pop_back();}max.push_back(num);push_heap(max.begin(),max.end(),less<int>());}}double GetMedian(){ int size = min.size() + max.size();double median = 0;if((size&0x1) == 1)median = min[0];elsemedian = (min[0]+max[0])/2;return median;}vector<double> min;vector<double> max;};这篇关于295. Find Median from Data Stream数据流中的中位数的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



