AVL树——左单旋、右单旋、左右双旋、右左双旋

本篇文章主要介绍AVL树的四种旋转方法。

首先，右单旋：

插入节点位于根节点的左子节点的左子树。

void _RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;Node* pparent = parent->_parent;subL->_parent = pparent;parent->_parent = subL;if (pparent == NULL)_root = subL;else{if (parent = pparent->_left)pparent->_left = subL;elsepparent->_right = subL;}parent->_bf = subL->_bf = 0;}

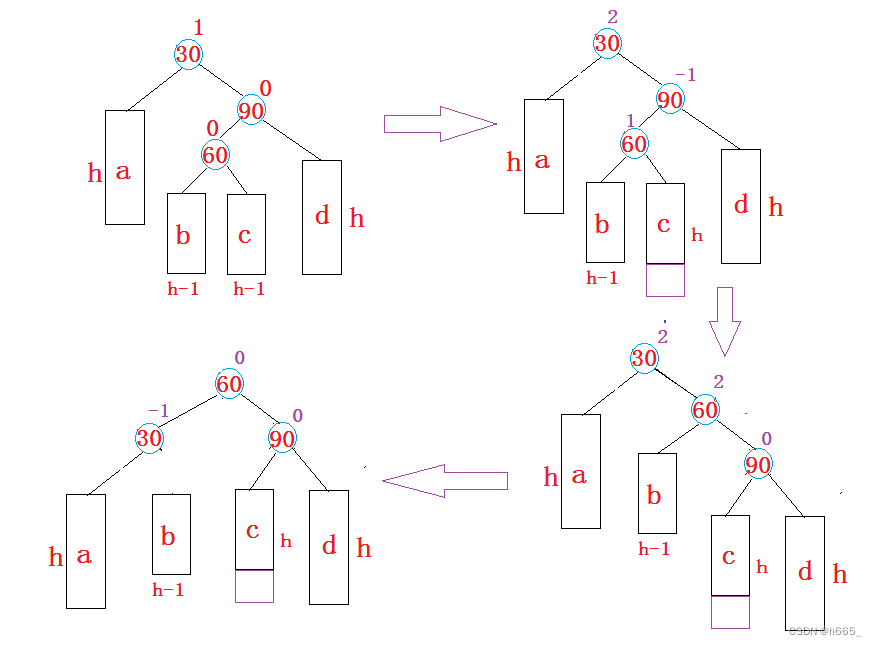
左单旋：

插入节点位于根节点的右子节点的右子树。

void  _RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;//处理节点parent->_right = subRL;if (subRL)subRL->_parent = parent;subR->_left = parent;Node* pparent = parent->_parent;subR->_parent = pparent;parent->_parent = subR;if (parent == _root)_root = subR;else{if (pparent->_left == parent)pparent->_left = subR;elsepparent->_right = subR;}parent->_bf = subR->_bf = 0;}

左右双旋：

插入节点位于根节点的左子节点的右子树。

void _RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;_RotateL(subL);_RotateR(parent);if (bf == 1)subL->_bf = -1;if (bf == -1)parent->_bf = 1;}

右左双旋：

插入节点位于根节点的右子节点的左子树。

void _RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;_RotateR(subR);_RotateL(parent);if (bf == 1)parent->_bf = -1;else if (bf == -1)subR->_bf = 1;}

接下来是AVL树的代码：

#pragma once
#include<iostream>
using namespace std;template <class K,class V>
struct AVLTreeNode
{AVLTreeNode(const K& key,const V& value):_left(NULL), _right(NULL),_parent(NULL), _key(key), _value(value), _bf(0){}AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;K _key;V _value;int _bf;
};template<class K,class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;public:AVLTree():_root(NULL){}bool Insert(const K& key,const  V& value){if (_root == NULL){_root = new Node(key, value);return true;}//找插入位置Node* cur = _root;Node* parent = NULL;while (cur){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}elsereturn false;}//插入cur = new Node(key, value);if (key < parent->_key)parent->_left = cur;elseparent->_right = cur;cur->_parent = parent;//更新双亲的平衡因子while (parent){if (parent->_left == cur)parent->_bf--;elseparent->_bf++;if (parent->_bf == 0)break;else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = cur->_parent;}else{if (parent->_bf == 2){if (cur->_bf == 1)_RotateL(parent);else_RotateRL(parent);}else{if (cur->_bf == -1)_RotateR(parent);else_RotateLR(parent);}break;}}return true;}void InOreder(){return _InOrder(_root);}bool IsBalance(){return _IsBalance(_root);}private:bool _IsBalance(Node* root){if (_root == NULL)return true;int LeftHight = _Hight(_root->_left);int RightHight = _Hight(_root->_right);if (abs(LeftHight - RightHight) >= 2)return false;return _IsBalance(_root->_left) && _IsBalance(_root->_right);}  int _Hight(Node* _root){if (_root == NULL)return 0;int LeftHight = _Hight(_root->_left)+1;int RightHight = _Hight(_root->_right)+1;return LeftHight > RightHight ? LeftHight+1 : RightHight+1;}void  _RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;//处理节点parent->_right = subRL;if (subRL)subRL->_parent = parent;subR->_left = parent;Node* pparent = parent->_parent;subR->_parent = pparent;parent->_parent = subR;if (parent == _root)_root = subR;else{if (pparent->_left == parent)pparent->_left = subR;elsepparent->_right = subR;}parent->_bf = subR->_bf = 0;}void _RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;Node* pparent = parent->_parent;subL->_parent = pparent;parent->_parent = subL;if (pparent == NULL)_root = subL;else{if (parent = pparent->_left)pparent->_left = subL;elsepparent->_right = subL;}parent->_bf = subL->_bf = 0;}void _RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;_RotateR(subR);_RotateL(parent);if (bf == 1)parent->_bf = -1;else if (bf == -1)subR->_bf = 1;}void _RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;_RotateL(subL);_RotateR(parent);if (bf == 1)subL->_bf = -1;if (bf == -1)parent->_bf = 1;}void _InOrder(Node* _root){if (_root){_InOrder(_root->_left);cout << " " << _root->_key << " " << _root->_value << endl;_InOrder(_root->_right);}}private:Node* _root;};void TestAVLTree()
{int array[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };AVLTree<int, int> t;for (int i = 0; i < sizeof(array) / sizeof(array[0]); i++){t.Insert(i, array[i]);}t.InOreder();if (t.IsBalance())cout << "平衡" << endl;elsecout << "不平衡" << endl;}