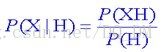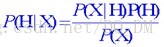第八章 朴素贝叶斯分类法

本文主要是介绍第八章 朴素贝叶斯分类法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言：贝叶斯分类包括朴素贝叶斯分类和贝叶斯信念网络分类。本章介绍朴素贝叶斯分类，第九章将会介绍贝叶斯信念网络分类。

1、贝叶斯定理

1.1 条件概率：

                                            

       P(X|H) 表示事件H已经发生的前提下，事件X发生的概率，叫做事件H发生下事件X的条件概率。

1.2 贝叶斯定理：

                                             

        P(H|X):后验概率，或在条件X下，H的后验概率。

        P(H)：先验概率，或H的先验概率。

        P(X|H)：条件H下，X的后验概率。

        P(X)：X的先验概率。

        贝叶斯定理之所以有用，是因为我们在生活中经常遇到这种情况：

                 很容易从给定的数据直接得出P(X)、P(H)和P(X|H)，却很难直接得出P(H|X)，但我们更关心P(H|X)。

        贝叶斯定理就为我们提供了从P(X)、P(H)和P(X|H)计算后验概率P(H|X)的方法。

2、朴素贝叶斯分类

        朴素贝叶斯分类法是一种简单的分类算法。

        朴素贝叶斯分类法的思想基础是这样的：对于给出的待分类项，求解此项在出现的条件下各个类别出现的概率，哪个最大，就认为此待分类项属于哪个类别。

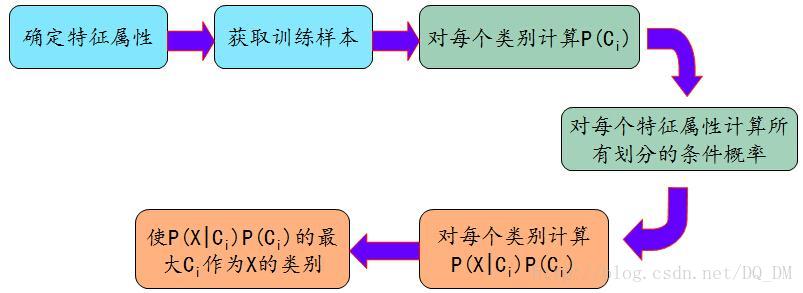
        朴素贝叶斯分类法的工作过程：

      （1）选定训练元组及其相关联的类标号集合记为D。每个元组用一个n维属性向量X={x₁,x₂,…,x_n}来表示，描述由n个属性A₁，A₂，...，A_n对元组的n个测量。

      （2）假定有m个类C₁，C₂，C₃，...，C_m。待分类元组X，分类法将预测X属于具有最大后验概率的类。即：若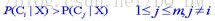，则X属于类 C_i 。

      （3）P(C_i|X)通过贝叶斯公式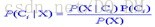来计算。由于P(X)对所有类为常数，故只需P(X|C_i)P(C_i)最大即可。

                如果先验概率P(C_i)未知，通常假定这些类是等概率的，即P(C₁)=...=P(C_m)。也可估算类先验概率P(C_i)= |C_i,D|/|D|，其中|C_i,D|是D中C_i类的训练元组数。

               为降低计算P(X|C_i)的开销，做类条件独立的朴素假定：假定属性值之间不存在依赖关系，则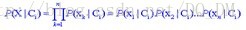。在计算P(X|C_i)时，应考虑每个属性A_k是分类的还是连续值的：

              （a）若A_k是分类属性，则P(x_k|C_i)=D中属性A_k值为x_k的C_i类的元组个数/D中C_i类的元组数|C_i,D|。

              （b）若A_k是连续值属性，则假定连续值属性服从均值为μ、标准差为σ的高斯分布（正态分布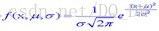）：，则P(x_k|C_i)=f(x_k,μ_Ci,σ_Ci)，其中μ_Ci（σ_Ci）表示在类C_i的情况下属性A_k的均值（方差）。

        朴素贝叶斯分类法的工作过程框架图：

                                                                

        朴素贝叶斯分类法的有效性：

        该分类法与决策树和神经网络分类法的各种比较试验表明，在某些领域，贝叶斯分类法具有最小的错误率。然而，实践中并非总是如此。这是由于对其使用的假定（如类条件独立性）的不正确性，以及缺乏可用的概率数据造成的。

        使用朴素贝叶斯分类预测类标号：

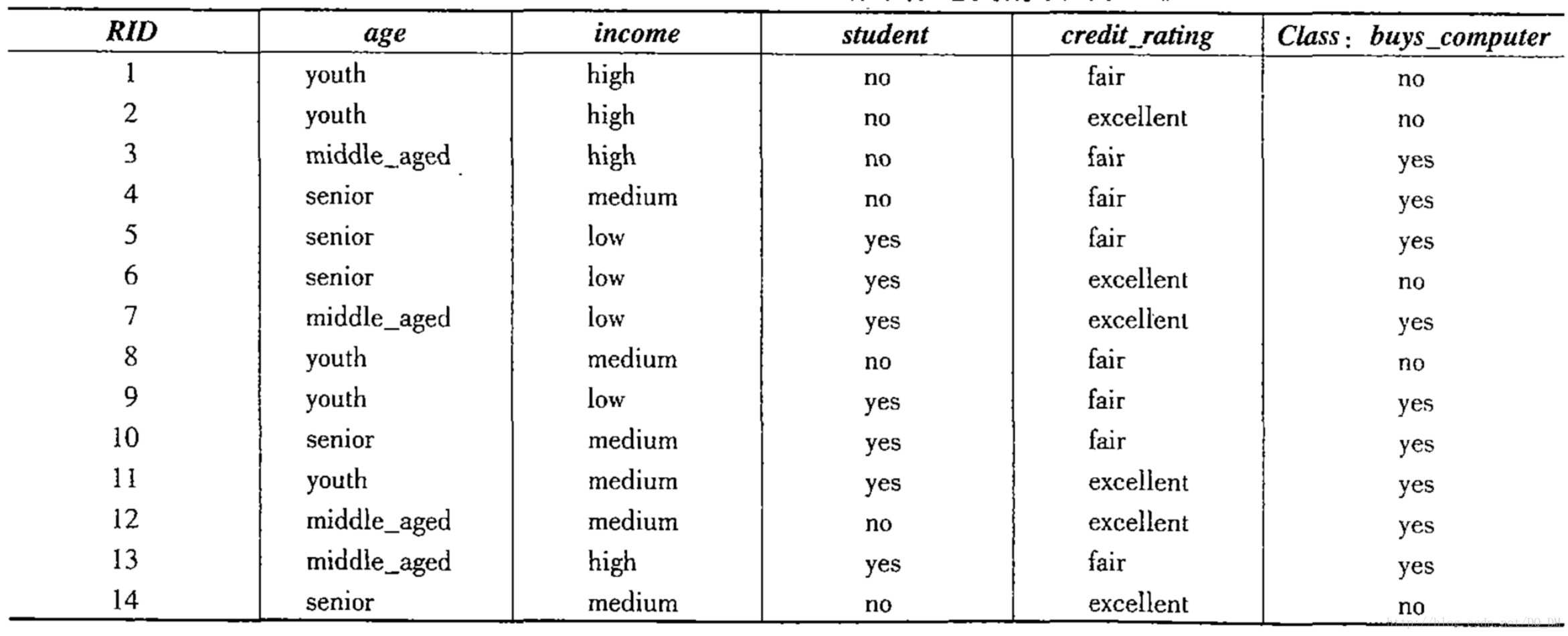
        训练数据如下表所示：

                                                               

        数据元组用属性age、income、student和credit_rating描述，

        类标号属性buys_computer具有两个不同值{ yes，no }。

        待分类的元组：X=（age= youth, income= medium, student= yes,credit_rating= fair）

      （1）根据训练元组计算每个类的先验概率P(C_i)：

                   P（buys_computer= yes ）=9/14=0.643

                   P（buys_computer= no ） =5/14=0.357

      （2）计算条件概率P(X|C_i),i=1、2，

                   P（age= youth | buys_computer= yes ）      =2/9=0.222

                   P（age= youth | buys_computer= no ）       =3/5=0.600

                   P（income= medium | buys_computer= yes） =4/9=0.444

                   P（income= medium | buys_computer= no） =2/5=0.400

                   P（student= yes | buys_computer= yes ）     =6/9=0.667

                   P（student= yes | buys_computer= no ）     =1/5=0.200

                   P（credit_rating= fair | buys_computer= yes） =6/9=0.667

                   P（credit_rating= fair | buys_computer= no ）=2/5=0.400

            从（2）中计算的概率得到：

                        P(X | buys_computer= yes)= P(age= youth | buys_computer= yes)

                                                                            ×P(income= medium | buys_computer= yes)

                                                                            ×P(student= yes | buys_computer= yes)

                                                                            ×P(credit_rating= yes | buys_computer= yes)

                                                                         =0.222×0.444×0.667×0.667 =0.044

            同理:

                     P(X | buys_computer= no) =0.600×0.400×0.200×0.400 =0.019

     （3）寻找最大化P(X|C_i)P(C_i)的类，计算：

                        P(X|buys_computer= yes)P(buys_computer=yes)=0.044×0.643=0.028

                        P(X|buys_computer= no)P(buys_computer=no)  =0.019×0.357=0.007

     （4）比较得出结果，元组X的类为buys_computer= yes

 

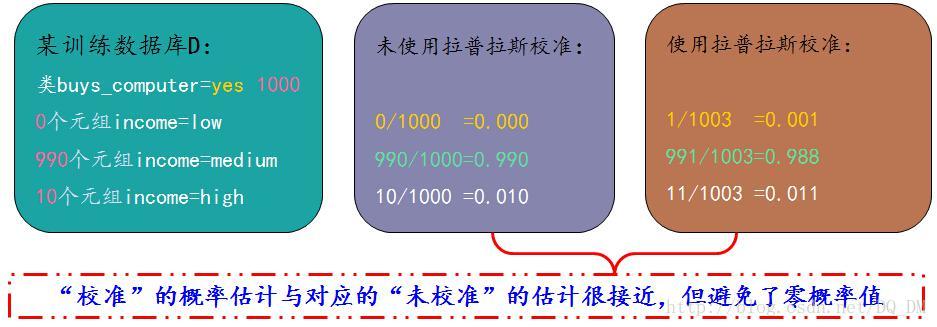
        如果遇到零概率值怎么办？

        如果得到某个P(x_k|C_i)的概率值为零，会发生什么？

        将这个零值代入上面的式中，将返回P(X|C_i)的概率为零，尽管没有这个零概率，仍然可能得到一个表明X属于C_i类的高概率。

        避免技巧：拉普拉斯校准/拉普拉斯估计法

        可以假定训练数据库D很大，以至于对每个计数加1造成的估计概率的变化可以忽略不计。如果对q个计数都加上1，则必须记住在用于计算概率的对应分母上加上q。用下面的例子解释这一技术。

 

这篇关于第八章 朴素贝叶斯分类法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---