本文主要是介绍北京交通大学Python课程设计大作业(一)——考虑红绿灯的北京市道路网上出租车导航及计费,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 北京交通大学Python课程设计大作业(一)——**考虑红绿灯的北京市道路网上出租车导航及计费**
- 一、课程设计目的
- 二、课程设计任务要求
- 三、方案一(基于实验五)
- 结果展示(未作可视化及图形界面交互)
- 四、基于Floyd算法
- 可视化运行效果展示
- 五、基于Dijkstra算法
- 可视化运行效果展示
- 六、总结体会感悟
北京交通大学Python课程设计大作业(一)——考虑红绿灯的北京市道路网上出租车导航及计费
一、课程设计目的
学校老师本着这样的目的:“本课程设计要求学生综合运用课程知识解决生活中的交通运输问题,培养学生应用计算机解决实际问题的思维方式,锻炼学生表达展示的能力。”
不得不说,大一的小朋友们这个时候对有向图可能都很陌生,更别说让自己搜集数据,绘制有向图并用字典或者Excel存储有向图数据。
笔者把大一的Python课程设计题目几乎做了个遍,如什么交通专业词典设计、地铁收费、出租车计费、词频统计等等(如果你的作业在这之中,快关注我!)然后发现,老师们留得作业内容几乎都差不多,这个作业虽然不难,但是挺麻烦,但是对于大一的小朋友们来说,我觉得还是很有难度的。
废话不多说,直接来看一下要求!由于笔者做的出租车的题目有两类,一类没有那么多交互以及计费优化方案等附加要求,一类不仅有这样要求,还要求设计图形界面可视化等。笔者在这里给出三种解决方案。
- 基于实验五《基于Python类的有向图时间、空间最短路径求解》的程序来完成这道题目基础要求
- 利用Floyd算法解决该程序设计
- 利用Dijkstra算法解决该程序设计
二、课程设计任务要求
以北京交通大学东门、南门和西门为起点,以中国农业科学院南门、北京理工大学北门、海淀公园东门、颐和园新建宫门、北京南站进站口、首都机场3号航站楼出发为终点。
根据百度地图或高德地图上的道路网构建导航有向图。要求:下图红色框内两个相邻红绿灯间的道路须表示为弧
红色框上每处红绿灯到导航终点须有至少一条弧;每条弧上带有属性长度、红绿灯数量、允许速度;有向图数据以文本或excel文件的形式存储。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-lEAHcDRA-1686310505106)(file:///C:/Users/ADMINI~1/AppData/Local/Temp/msohtmlclip1/01/clip_image002.jpg)]](https://img-blog.csdnimg.cn/f3ef90f74f81470d9bcf3141856b3729.png)
参考实验5《基于Python类的有向图时间、空间最短路径求解》的要求,从有向图定义文件中读取有向图数据,规划以任务1中各起点到各终点的最短路径,并计算相应的最短距离和等待时间。导航过程中,碰上红灯和绿灯的可能性相同,如果为红灯,则等待的时间为0-60秒间的随机数。
根据如下出租车计费规则,计算各起点到各终点的出租车费用。出租车计费规则:(1)车价=起步价(13元) (里程数<3);(2)车价=起步价(13元)+(里程数 - 起步里程数(3公里))*每公里单价(2.3元) (里程数<10);(3)车价=起步价(13元)+(远程里程标准(10公里) - 起步里程数(3公里))*每公里单价 + (里程数 - 远程里程标准(10)) *远程每公里单价(3.2元) (里程数>10);(4)燃油附加费标准为每运次1元;(5)等待红绿灯时间每5分钟按1公里计费。
增加附加功能:优化方案
当打车在19公里以上时,不到15 公里时下来换一辆车(或者,请司机重新打表*_*,一般司机会同意的),总费用不变。超过19公里时这样打车,则每超过一公里可以节省一块。
不算等时,如果总里程在30公里,打两个15公里是68,而一个30公里则是79。
如果算上等时则多更多。如果总里程在60公里,打4个15公里是136,一个60公里则是169。如果再算上40分钟等时,平均分布在全路段,则前者是152,后者是191,相差近40块钱
输出各起点到各终点的路径、等待时间、打车费用和费用构成。
三、方案一(基于实验五)
存在txt纯文本文件当中,存为字典数据类型。未做可视化展示和图形界面交互,直接在控制台交互,增加了递归和异常处理操作,确保无论如何输入都不会报错!
import random as r# 记录查询历史
class TextRecord(object):def __init__(self):self.filepath = '查询记录文本文件.txt'# 记录查询记录def record(self, text):with open(self.filepath, 'a+', encoding='utf-8') as file:file.write(text)# 记录输出def recordShow(self):try:with open(self.filepath, 'r', encoding='utf-8') as file:text = file.read()print(text)except:print("暂无查询记录!")# 定义Path类
class Path(object):def __init__(self, path, distancecost, timecost):self.__path = pathself.__distancecost = distancecostself.__timecost = timecost# 路径上最后一个节点def getLastNode(self):return self.__path[-1]# 判断node是否为路径上最后一个节点def isLastNode(self, node):return node == self.getLastNode()# 增加加点和成本产生一个新的path对象def addNode(self, node, dprice, tprice):return Path(self.__path + [node], self.__distancecost + dprice, self.__timecost + tprice)self.__timecost = self.__timecost + pricereturn Path(self.__path + [node], self.__distancecost, self.__timecost)# 输出当前路径def printPath(self):for n in self.__path:if self.isLastNode(n):print(n)else:print(n, end="->")print(f"最短路径距离{self.__distancecost:.2f}km")print(f"红绿灯个数 {self.__timecost:.0f}个")self.text = f"最短路径距离{self.__distancecost:.2f}km\n红绿灯个数 {self.__timecost:.0f}个\n"@propertydef dcost(self):return self.__distancecost@propertydef tcost(self):return self.__timecost# 获取路径路径@propertydef path(self):return self.__path# 获取路径总成本的只读属性@propertydef travelCost(self):return self.__distancecost# 定义DirectedGraph类
class DirectedGraph(object):def __init__(self, d):if isinstance(d, dict):self.__graph = dself.recorder = TextRecord()else:self.__graph = dict()print('数据读取错误!请查看数据格式是否正确。')# 通过递归生成所有可能的路径def __generatePath(self, graph, path, end, results, costIndex):current = path.getLastNode()if current == end:results.append(path)else:for n in graph[current]:if n not in path.path:self.__generatePath(graph, path.addNode(n, self.__graph[path.getLastNode()][n][0], self.__graph[path.getLastNode()][n][1]), end, results, costIndex)# 计算价格部分def calculate_price(self, distance, trafic_lights_number, base_price=13, start_distance=3, long_distance=10,long_distance_price=3.2,short_distance_price=2.3, fuel_surcharge=1): # 根据距离计算车费total_price = 0dis_price = 0 # 里程收费tim_price = 0 # 等待时间收费wait_time = 0for i in range(trafic_lights_number):red_light = 1 * r.randint(0, 1)wait_time += red_light * r.randint(1, 60)self.timecost = wait_time / 60wait_time = wait_time / 300 # 模拟红绿灯等待时间换算成等效里程# 里程收费if distance <= start_distance: # 短途车程dis_price += base_priceelif start_distance < distance <= long_distance:dis_price += base_price + (distance - start_distance) * short_distance_price # 常规车程else:dis_price += base_price + (long_distance - start_distance) * short_distance_price + (distance - long_distance) * long_distance_price# 红绿灯等待时间换算成等效里程收费if 1 <= wait_time <= start_distance:tim_price += base_priceelif start_distance < wait_time <= long_distance:tim_price += base_price + (wait_time - start_distance) * short_distance_price # 常规车程elif wait_time > long_distance:tim_price += base_price + (long_distance - start_distance) * short_distance_price + (wait_time - long_distance) * long_distance_price# 加上燃油费total_price += dis_price + tim_price + fuel_surchargereturn dis_price, tim_price, total_price# 搜索start到end之间时间或空间最短的路径,并输出def __searchPath(self, start, end, costIndex):results = []self.__generatePath(self.__graph, Path([start], 0, 0), end, results, costIndex)if costIndex == 0:results.sort(key=lambda p: p.dcost)elif costIndex == 1:results.sort(key=lambda p: p.tcost)print(f'{"最短路径" if costIndex == 0 else "最短时间路径"}', start, '->', end, '为:', end="")results[0].printPath()dis_price, tim_price, total_price = self.calculate_price(results[0].dcost, results[0].tcost)print(f"等待时间为{self.timecost:.2f}min\n总消费为:{total_price:.2f}元\n分别为:\n里程收费{dis_price:.2f}元,等待时长收费{tim_price:.2f}元")text = f'{"最短路径" if costIndex == 0 else "最短时间路径"}{start}->{end}为:\n' + results[0].text + '\n' + f"等待时间为{self.timecost:.2f}min\n总消费为:{total_price:.2f}元\n分别为:\n里程收费{dis_price:.2f}元,等待时长收费{tim_price:.2f}元\n"self.recorder.record(text)# 调用__searchPath搜索start到end之间的空间最短的路径,并输出def searchSpatialMinPath(self, start, end):self.__searchPath(start, end, 0)# 调用__searchPath搜索start到end之间的时间最短的路径,并输出def searchTemporalMinPath(self, start, end):self.__searchPath(start, end, 1)# 线路查询模块def pathQuery(self, fname, start_node, end_node):strs = "_" * 20# 文件读取,数据提取with open(fname, 'r', encoding='utf-8') as f:# (空间距离,时间距离)graphy_dict = eval(f.read())# 起始点列表print(f"{strs}请输入起始点{strs}")i = 0try:for start in start_node:print(f"{i}-{start}")i += 1node0 = int(input(":请输入对应序号:"))startnode = start_node[node0]print(f"{strs}请输入终点{strs}")k = 0for end in end_node:print(f"{k}-{end}")k += 1node1 = int(input(":请输入对应序号:"))endnode = end_node[node1]# 实例化对象g1 = DirectedGraph(graphy_dict)print(f"{strs}{startnode}->{endnode}{strs}")g1.searchSpatialMinPath(startnode, endnode)print(f"{strs}{strs}")g1.searchTemporalMinPath(startnode, endnode)except:print("输入错误!请重新输入")self.pathQuery(fname, start_node, end_node)# 记录查询def recordQuery(self):self.recorder.recordShow()# 模式选择def modeSelect(self, fname, start_node, end_node):select = int(input("0-最短路径计费查询模式\n1-查看查询历史:"))if select == 0:self.pathQuery(fname, start_node, end_node)elif select == 1:self.recordQuery()else:print("输入指令错误!请重新输入")self.modeSelect(fname, start_node, end_node)selsect2 = int(input("0-退出程序\n1-继续执行:"))if selsect2 == 0:return 0elif selsect2 == 1:self.modeSelect(fname, start_node, end_node)# 脚本自调试
if __name__ == '__main__':# 有向图数据文件路径filename = 'try.txt'# 起始点列表start_node = ['交大东门', '交大西门', '交大南门']end_node = ['中国农业科学院南门', '北理工北门', '海淀公园东门', '颐和园新建宫门', '北京南站进站口', '首都机场3号航站楼']# 打开文件with open(filename, 'r', encoding='utf-8') as f:dicts = eval(f.read())# 实例化对象test = DirectedGraph(dicts)# 模式选择test.modeSelect(filename, start_node, end_node)结果展示(未作可视化及图形界面交互)
C:\Users\Administrator\AppData\Local\Programs\Python\Python36\python.exe E:/python/大一python课程设计/tryss.py
0-最短路径计费查询模式
1-查看查询历史:0
____________________请输入起始点____________________
0-交大东门
1-交大西门
2-交大南门
:请输入对应序号:0
____________________请输入终点____________________
0-中国农业科学院南门
1-北理工北门
2-海淀公园东门
3-颐和园新建宫门
4-北京南站进站口
5-首都机场3号航站楼
:请输入对应序号:1
____________________交大东门->北理工北门____________________
最短路径 交大东门 -> 北理工北门 为:交大东门->交大西门->6->9->10->11->北理工北门
最短路径距离4.61km
红绿灯个数 4个
等待时间为0.82min
总消费为:17.70元
分别为:
里程收费16.70元,等待时长收费0.00元
________________________________________
最短时间路径 交大东门 -> 北理工北门 为:交大东门->交大西门->6->8->中国农业科学院南门->10->11->北理工北门
最短路径距离4.99km
红绿灯个数 4个
等待时间为0.00min
总消费为:18.59元
分别为:
里程收费17.59元,等待时长收费0.00元
0-退出程序
1-继续执行:1
0-最短路径计费查询模式
1-查看查询历史:0
____________________请输入起始点____________________
0-交大东门
1-交大西门
2-交大南门
:请输入对应序号:2
____________________请输入终点____________________
0-中国农业科学院南门
1-北理工北门
2-海淀公园东门
3-颐和园新建宫门
4-北京南站进站口
5-首都机场3号航站楼
:请输入对应序号:4
____________________交大南门->北京南站进站口____________________
最短路径 交大南门 -> 北京南站进站口 为:交大南门->3->2->北京南站进站口
最短路径距离13.77km
红绿灯个数 15个
等待时间为4.68min
总消费为:42.16元
分别为:
里程收费41.16元,等待时长收费0.00元
________________________________________
最短时间路径 交大南门 -> 北京南站进站口 为:交大南门->交大东门->5->3->2->北京南站进站口
最短路径距离14.77km
红绿灯个数 13个
等待时间为2.97min
总消费为:45.37元
分别为:
里程收费44.37元,等待时长收费0.00元
0-退出程序
1-继续执行:1
0-最短路径计费查询模式
1-查看查询历史:1
最短路径交大南门->北京南站进站口为:
最短路径距离13.77km
红绿灯个数 15个等待时间为2.37min
总消费为:42.16元
分别为:
里程收费41.16元,等待时长收费0.00元
最短时间路径交大南门->北京南站进站口为:
最短路径距离14.77km
红绿灯个数 13个等待时间为3.43min
总消费为:45.37元
分别为:
里程收费44.37元,等待时长收费0.00元
最短路径交大南门->北京南站进站口为:
最短路径距离13.77km
红绿灯个数 15个等待时间为2.47min
总消费为:42.16元
分别为:
里程收费41.16元,等待时长收费0.00元
最短时间路径交大南门->北京南站进站口为:
最短路径距离14.77km
红绿灯个数 13个等待时间为4.03min
总消费为:45.37元
分别为:
里程收费44.37元,等待时长收费0.00元
最短路径交大南门->北京南站进站口为:
最短路径距离13.77km
红绿灯个数 15个等待时间为5.02min
总消费为:55.16元
分别为:
里程收费41.16元,等待时长收费13.00元
最短时间路径交大南门->北京南站进站口为:
最短路径距离14.77km
红绿灯个数 13个等待时间为4.13min
总消费为:45.37元
分别为:
里程收费44.37元,等待时长收费0.00元
最短路径交大西门->颐和园新建宫门为:
最短路径距离10.51km
红绿灯个数 15个等待时间为5.65min
总消费为:44.73元
分别为:
里程收费30.73元,等待时长收费13.00元
最短时间路径交大西门->颐和园新建宫门为:
最短路径距离12.77km
红绿灯个数 11个等待时间为3.73min
总消费为:38.96元
分别为:
里程收费37.96元,等待时长收费0.00元
最短路径交大东门->中国农业科学院南门为:
最短路径距离2.86km
红绿灯个数 2个等待时间为0.43min
总消费为:14.00元
分别为:
里程收费13.00元,等待时长收费0.00元
最短时间路径交大东门->中国农业科学院南门为:
最短路径距离2.86km
红绿灯个数 2个等待时间为1.02min
总消费为:14.00元
分别为:
里程收费13.00元,等待时长收费0.00元
最短路径交大东门->北理工北门为:
最短路径距离4.61km
红绿灯个数 4个等待时间为1.40min
总消费为:17.70元
分别为:
里程收费16.70元,等待时长收费0.00元
最短时间路径交大东门->北理工北门为:
最短路径距离4.99km
红绿灯个数 4个等待时间为0.93min
总消费为:18.59元
分别为:
里程收费17.59元,等待时长收费0.00元
最短路径交大东门->海淀公园东门为:
最短路径距离9.80km
红绿灯个数 15个等待时间为2.38min
总消费为:29.64元
分别为:
里程收费28.64元,等待时长收费0.00元
最短时间路径交大东门->海淀公园东门为:
最短路径距离12.21km
红绿灯个数 9个等待时间为1.73min
总消费为:37.18元
分别为:
里程收费36.18元,等待时长收费0.00元
最短路径交大南门->首都机场3号航站楼为:
最短路径距离32.77km
红绿灯个数 8个等待时间为3.13min
总消费为:102.96元
分别为:
里程收费101.96元,等待时长收费0.00元
最短时间路径交大南门->首都机场3号航站楼为:
最短路径距离36.72km
红绿灯个数 5个等待时间为1.32min
总消费为:115.61元
分别为:
里程收费114.61元,等待时长收费0.00元
最短路径交大东门->北理工北门为:
最短路径距离4.61km
红绿灯个数 4个等待时间为0.82min
总消费为:17.70元
分别为:
里程收费16.70元,等待时长收费0.00元
最短时间路径交大东门->北理工北门为:
最短路径距离4.99km
红绿灯个数 4个等待时间为0.00min
总消费为:18.59元
分别为:
里程收费17.59元,等待时长收费0.00元
最短路径交大南门->北京南站进站口为:
最短路径距离13.77km
红绿灯个数 15个等待时间为4.68min
总消费为:42.16元
分别为:
里程收费41.16元,等待时长收费0.00元
最短时间路径交大南门->北京南站进站口为:
最短路径距离14.77km
红绿灯个数 13个等待时间为2.97min
总消费为:45.37元
分别为:
里程收费44.37元,等待时长收费0.00元0-退出程序
1-继续执行:1
0-最短路径计费查询模式
1-查看查询历史:0
____________________请输入起始点____________________
0-交大东门
1-交大西门
2-交大南门
:请输入对应序号:4
输入错误!请重新输入
____________________请输入起始点____________________
0-交大东门
1-交大西门
2-交大南门
:请输入对应序号:2
____________________请输入终点____________________
0-中国农业科学院南门
1-北理工北门
2-海淀公园东门
3-颐和园新建宫门
4-北京南站进站口
5-首都机场3号航站楼
:请输入对应序号:4
____________________交大南门->北京南站进站口____________________
最短路径 交大南门 -> 北京南站进站口 为:交大南门->3->2->北京南站进站口
最短路径距离13.77km
红绿灯个数 15个
等待时间为4.35min
总消费为:42.16元
分别为:
里程收费41.16元,等待时长收费0.00元
________________________________________
最短时间路径 交大南门 -> 北京南站进站口 为:交大南门->交大东门->5->3->2->北京南站进站口
最短路径距离14.77km
红绿灯个数 13个
等待时间为3.18min
总消费为:45.37元
分别为:
里程收费44.37元,等待时长收费0.00元
0-退出程序
1-继续执行:0进程已结束,退出代码为 0
查询记录被存入“查询记录文本文件.txt“文件当中。
四、基于Floyd算法
存在Excel文件当中,存为DatFrame表格数据类型
有向图数据格式如下:(由于该数据是笔者自己搜集的,已经被一些同学用过,故可大方展示出来,不过尽量不要直接拿走用!!)
| 交大东门 | 交大南门 | 交大西门 | 1 | 2 | 3 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 中国农业科学院南门 | 北理工北门 | 海淀公园东门 | 颐和园新建宫门 | 北京南站进站口 | 首都机场3号航站楼 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 交大东门 | [0.781,0] | [1.1,0] | [0.54,1] | ||||||||||||||||||||
| 交大南门 | [0.781,0] | [0.614,0] | [0.8,3] | [0.61,1] | |||||||||||||||||||
| 交大西门 | [1.1,0] | [0.614,0] | [0.11,0] | ||||||||||||||||||||
| 1 | [1.5,2] | [7.8,4] | |||||||||||||||||||||
| 2 | [2.28,4] | [12.4,10] | [31.4,3] | ||||||||||||||||||||
| 3 | [0.57,2] | ||||||||||||||||||||||
| 5 | [0.36,0] | [0.61,1] | [0.66,1] | ||||||||||||||||||||
| 6 | [0.11,0] | [0.594,1] | [1,1] | ||||||||||||||||||||
| 7 | [1.3,2] | [32.2,6] | |||||||||||||||||||||
| 8 | [0.93,3] | [1.02,2] | [1.1,2] | [1.06,1] | |||||||||||||||||||
| 9 | [0.59,1] | ||||||||||||||||||||||
| 10 | [1.21,2] | [1.19,2] | [0.32,0] | ||||||||||||||||||||
| 11 | [0.6,1] | [0.6,0] | |||||||||||||||||||||
| 12 | [1.23,2] | [6.4,8] | |||||||||||||||||||||
| 13 | [1.19,2] | ||||||||||||||||||||||
| 14 | [0.37,2] | [34.1,2] | |||||||||||||||||||||
| 15 | [0.22,0] | [7,5] | [7,10] | ||||||||||||||||||||
| 中国农业科学院南门 | [0.32,0] | ||||||||||||||||||||||
| 北理工北门 | |||||||||||||||||||||||
| 海淀公园东门 | |||||||||||||||||||||||
| 颐和园新建宫门 | |||||||||||||||||||||||
| 北京南站进站口 | |||||||||||||||||||||||
| 首都机场3号航站楼 |
import pandas as pd, numpy as np, matplotlib.pyplot as plt, networkx as nx, copy, random as r, datetime
from tkinter import *# 出租车导航最短路径、等待时间和收费计算模块
class Shortest_path_pro(object):# 初始化函数def __init__(self, filepath):# 无穷大表示self.M = np.inf# 获取权矩阵self.weight_df = self.get_weight_df(filepath)# 获取路径矩阵self.S_df = self.get_S_df()# 获取路径矩阵[self.last_weight_df, self.last_S_df] = self.Floyd(copy.deepcopy(self.weight_df), self.S_df)# 展示Floyd算法迭代结果print("利用Floyd算法计算过程如下")strs = "-" * 20key_list = [key for key in self.weigth_df_dict.keys()]key1_list = [key1 for key1 in self.S_df_dict.keys()]for k in range(len(key_list)):print(f"{strs}{key_list[k]}{strs}")print(self.weigth_df_dict[key_list[k]].replace(self.M, "∞"))print(f"{strs}{key1_list[k]}{strs}")print(self.S_df_dict[key1_list[k]])print(f"{strs}迭代完成{strs}")# 获取路径矩阵def get_S_df(self):S_df = pd.DataFrame([[i + 1 for i in range(len(self.weight_df.index.tolist()))] for j inrange(len(self.weight_df.index.tolist()))],index=[f"Node{i + 1}" for i in range(len(self.weight_df.index.tolist()))],columns=[f"Node{i + 1}" for i in range(len(self.weight_df.index.tolist()))])return S_df# 获取权矩阵def get_weight_df(self, filepath):self.weight_edge_list = []self.df = pd.read_excel(filepath)index = self.df.iloc[:, 0].tolist()self.node = indexself.node_number = len(index)self.df = self.df.iloc[:, 1:]self.df.index = indexfor i in range(len(index)):for j in range(len(index)):if i == j:self.df.iloc[i, j] = "[0,0]"self.graphy_df = self.dfW_df = pd.DataFrame(index=[f"Node{i + 1}" for i in range(len(index))],columns=[f"Node{i + 1}" for i in range(len(index))])for i in range(len(index)):for j in range(len(index)):try:W_df.iloc[i, j] = eval(self.df.iloc[i, j])[0]if eval(self.df.iloc[i, j])[0] != 0:self.weight_edge_list.append((index[i], index[j], eval(self.df.iloc[i, j])[0]))except:passW_df = W_df.replace(np.nan, self.M)return W_df# Floyd算法实现def Floyd(self, weight_df0, S_df0):n = self.node_numberself.weigth_df_dict = {"D(0)": weight_df0}self.S_df_dict = {"S(0)": S_df0}k = 1while k <= n:next_weight_df = pd.DataFrame(index=[f"Node{i + 1}" for i in range(n)],columns=[f"Node{j + 1}" for j in range(n)])next_S_df = pd.DataFrame(index=[f"Node{i + 1}" for i in range(n)],columns=[f"Node{j + 1}" for j in range(n)])for i in range(n):for j in range(n):next_weight_df.iloc[i, j] = min([weight_df0.iloc[i, j], weight_df0.iloc[i, k - 1] + weight_df0.iloc[k - 1, j]])for i in range(n):for j in range(n):if weight_df0.iloc[i, j] <= weight_df0.iloc[i, k - 1] + weight_df0.iloc[k - 1, j]:next_S_df.iloc[i, j] = S_df0.iloc[i, j]elif weight_df0.iloc[i, j] > weight_df0.iloc[i, k - 1] + weight_df0.iloc[k - 1, j]:next_S_df.iloc[i, j] = S_df0.iloc[i, k - 1]weight_df0 = next_weight_dfS_df0 = next_S_dfself.weigth_df_dict.update({f"D({k})": weight_df0})self.S_df_dict.update({f"S({k})": S_df0})k += 1return [weight_df0, S_df0]# 获取最短路径和长度def get_shortest_path(self, start_node, end_node):length = self.last_weight_df.iloc[start_node - 1, end_node - 1]path_list = [start_node]while 1:if self.last_S_df.iloc[start_node - 1, end_node - 1] != end_node:path_list.append(self.last_S_df.iloc[start_node - 1, end_node - 1])start_node = self.last_S_df.iloc[start_node - 1, end_node - 1]else:path_list.append(self.last_S_df.iloc[start_node - 1, end_node - 1])breakshortestpath = []for node in path_list:shortestpath.append(self.node[node - 1])print("最短路径为:")i = 1n = len(shortestpath)for node in shortestpath:if i < n:print(f"{node}->", end="")i += 1else:print(node, end="")print("")return [path_list, length, shortestpath]# 等待时间消费def get_time_cost(self, pathlist):n = len(pathlist)timecost = 0for i in range(n - 1):timecost += eval(self.df.iloc[pathlist[i] - 1, pathlist[i + 1] - 1])[1]return timecost# 绘制网络——可视化展现,生成路网异构图def network_graph(self, weight_edge_list, shortest_path):factnode = []for sp in shortest_path:factnode.append(self.node[sp - 1])shortest_path_list = factnode# 忽略除以0的报错np.seterr(divide='ignore', invalid='ignore')# 用来正常显示中文plt.rcParams['font.sans-serif'] = ['SimHei']# 用来正常显示负号plt.rcParams['axes.unicode_minus'] = FalseG2 = nx.DiGraph() # 创建:空的 有向图G2.add_weighted_edges_from(weight_edge_list) # 添加 带权边,weight表示边权# 添加 带权边,weight表示边权pos = nx.spring_layout(G2) # 用 FR算法排列节点nx.draw(G2, pos, with_labels=True, alpha=0.5)labels = nx.get_edge_attributes(G2, 'weight')nx.draw_networkx_edge_labels(G2, pos, edge_labels=labels)edgeList = []for i in range(len(shortest_path_list) - 1):edgeList.append((shortest_path_list[i], shortest_path_list[i + 1]))nx.draw_networkx_edges(G2, pos, edgelist=edgeList, edge_color='m', width=4) # 设置边的颜色plt.show()# 打车费用(增加附加功能优化方案)def taxi_fare(self, distance, wait_time0):# 总里程小于19if distance < 19:wait_time = (wait_time0 * r.randint(1, 60)) / 300# 空间距离费用disfee = 0waitfee = 0if 0 <= distance <= 3:disfee += 13 + 1elif 3 < distance <= 10:disfee += 13 + 2.3 * (distance - 3) + 1elif distance > 10:disfee += 13 + 2.3 * (10 - 3) + (distance - 10) * 3.2 + 1# 等待时长换算成等效里程费用equivalent_mileage = wait_timeif 1 <= equivalent_mileage <= 3:waitfee += 13elif 3 < equivalent_mileage <= 10:waitfee += 13 + 2.3 * (equivalent_mileage - 3)elif equivalent_mileage > 10:waitfee += 13 + 2.3 * (10 - 3) + (equivalent_mileage - 10) * 3.2# 总里程大于19elif distance > 19:disfee = 0waitfee = 0# 总里程大于19小于30if distance < 30:disfee, waitfee = self.taxi_fare(15, wait_time0)extr_disfee, extr_waitfee = self.taxi_fare(distance - 15, wait_time0)disfee, waitfee = disfee + extr_disfee, (waitfee + extr_waitfee) / 2# 总里程大于30小于60elif 30 <= distance < 60:# 三目运算操作,使代码更加简洁disfee = 68 + ((distance - 30) / 30) * 79 if self.taxi_fare(15, wait_time0)[1] < 20 else 72 + ((distance - 30) / 30) * 83waitfee = self.taxi_fare(15, wait_time0)[1]# 总里程大于60elif distance >= 60:# 三目运算操作,使代码更加简洁disfee = 136 + ((distance - 60) / 60) * 169 if self.taxi_fare(15, wait_time0)[1] < 40 else 152 + ((distance - 60) / 60) * 191waitfee = self.taxi_fare(15, wait_time0)[1]return [disfee, waitfee]# 图形界面类模块
class GraphicalInterface(object):# 初始化函数def __init__(self, filepath):# 创建记录数据的文件夹self.record_txt = '输入记录.txt'# 实例化Shortest_path_pro类对象self.short = Shortest_path_pro(filepath)# 创建tk窗口self.tk = Tk()self.tk.title('考虑红绿灯的北京市道路网上出租车导航及计费')self.tk.geometry('500x500')# 输入框1self.now_nub1 = Label(self.tk, text='1、请输入起点:')self.now_nub1.grid(row=1, column=1, sticky='E')self.now_bok1 = Spinbox(self.tk, values=['交大东门', '交大南门', '交大西门'], width=25)self.now_bok1.grid(row=1, column=2, sticky='NW')# 输入框2self.now_nub2 = Label(self.tk, text='2、请输入终点:')self.now_nub2.grid(row=2, column=1, sticky='E')self.now_bok2 = Spinbox(self.tk, values=['中国农业科学院南门', '北京理工大学北门', '海淀公园东门', '颐和园新建宫门', '北京南站进站口', '首都机场3号航站楼'],width=25)self.now_bok2.grid(row=2, column=2, sticky='NW')# 输出结果self.Output_results = Label(self.tk, text='输出结果:')self.Output_results.grid(row=8, column=1, sticky='NW')self.result_data_Text = Text(self.tk, width=40, height=30)self.result_data_Text.grid(row=10, column=2, rowspan=15, columnspan=10)self.main()# 图形界面形成def graphicalInterface(self):strs = "-" * 20startnode = {'交大东门': 1, '交大南门': 2, '交大西门': 3}[self.now_bok1.get()]endnode = {'中国农业科学院南门': 18, '北京理工大学北门': 19, '海淀公园东门': 20, '颐和园新建宫门': 21, '北京南站进站口': 22, '首都机场3号航站楼': 23}[self.now_bok2.get()]# 由self.short对象获取最短路径及最短路径长度[shortest_path, shortest_length, fact_shortest_path] = self.short.get_shortest_path(startnode, endnode)print(f"最短路径长度为:{shortest_length:.2f}km")# 形成窗口弹出文案path = ''i = 1n = len(fact_shortest_path)for node in fact_shortest_path:if i < n:path += f"{node}->"i += 1else:path += f"{node}"# 费用构成disfee = self.short.taxi_fare(shortest_length, self.short.get_time_cost(shortest_path))[0]waitfee = self.short.taxi_fare(shortest_length, self.short.get_time_cost(shortest_path))[1]# 获取当前电脑时间(格式化后的时间:××××-××-××)times = datetime.datetime.now().strftime('%Y-%m-%d')# 形成文案,使用字符串格式化操作text = f"{strs}记录时间{times}{strs}\n{strs}{self.now_bok1.get()}->{self.now_bok2.get()}{strs}\n最短路径为:\n{path}\n最短路径长度为:{shortest_length:.2f}km\n等待时间为:{self.short.get_time_cost(shortest_path)}min\n打车费用为:{disfee + waitfee:.2f}元\n费用构成分别为:空间里程收费{disfee:.2f}元和等待时长收费{waitfee:.2f}元\n{strs}{strs}\n"self.result_data_Text = Label(self.tk, text=text)self.result_data_Text.grid(row=10, column=2, rowspan=15, columnspan=3)self.short.network_graph(self.short.weight_edge_list, shortest_path)# 追加写如文件,记录操作with open(self.record_txt, 'a+', encoding='utf-8') as f:f.write(text)# 主程序(点击操作)def main(self):AnNiu = Button(self.tk, text='形成线网可视化图', fg='blue', bd=3, width=20, command=self.graphicalInterface)AnNiu.grid(row=5, column=2, sticky='NW')self.tk.mainloop()# 脚本自调试
if __name__ == '__main__':strs = "-" * 20# 文件路径filepath = "Directed graph.xlsx"# 实例化对象test = GraphicalInterface(filepath)可视化运行效果展示
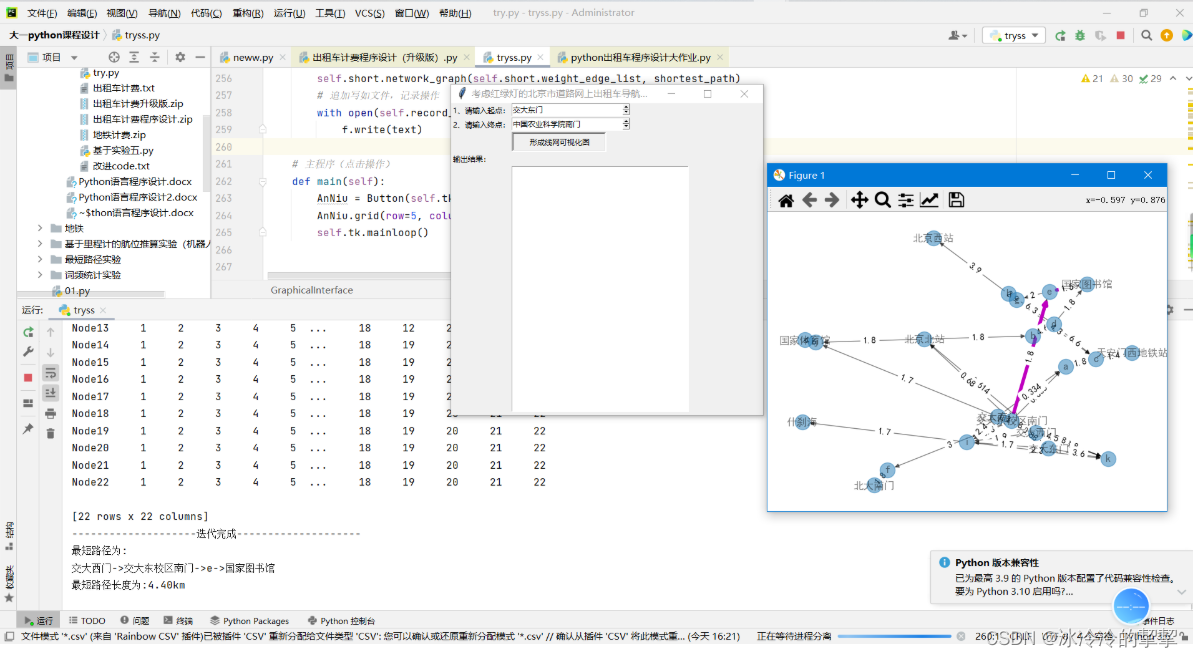
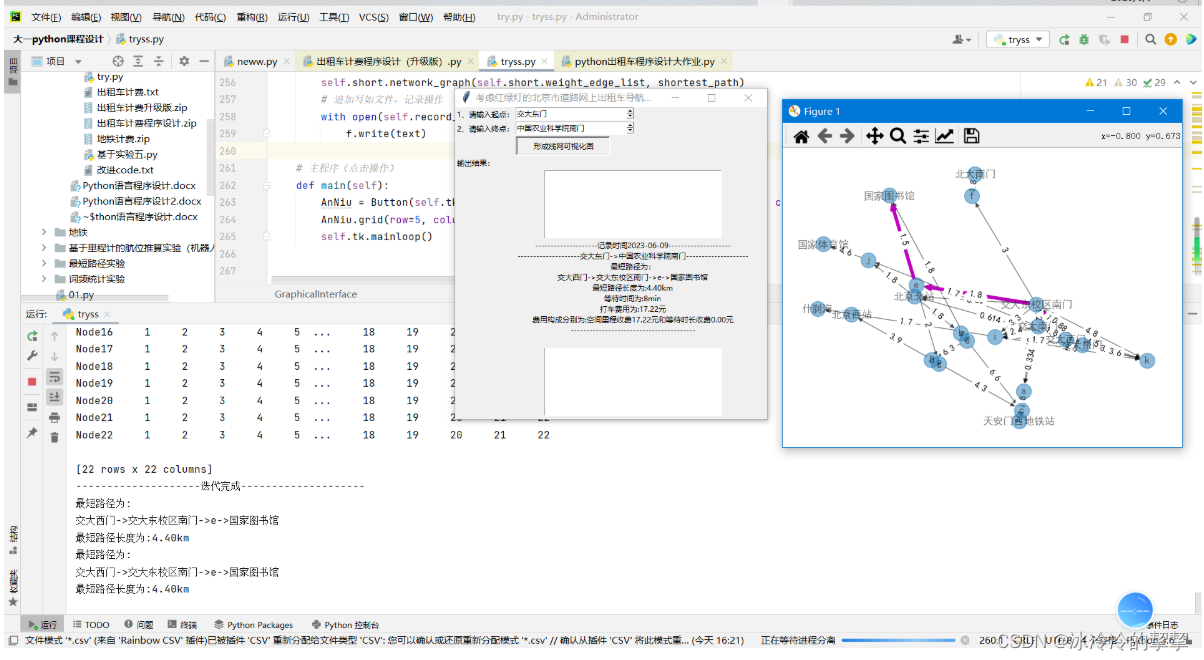
查询记录同样记录着文本文件当中。
五、基于Dijkstra算法
利用txt文本文件存储有向图数据,存为字典数据类型,如下图所示(数据是一些同学自己找的,故于此处加码保密)

import pandas as pd, numpy as np, matplotlib.pyplot as plt, networkx as nx, datetime, random as r
from tkinter import *# 构造有向图Graph
class Graph(object):def __init__(self, graph, start, end): # labels为标点名称self.G = graphself.startnode = startself.endnode = end# 算法实现def Dijkstra(self, v0, INF=np.inf): # 999表示该结点到起始点的距离还没有一个确切的值dis = dict((i, INF) for i in self.G.keys()) # 初始化一个距离表,这个表记录着起始结点v0到图中各个点的距离current_node = v0 # 一开始,当前点设置为起始点v0dis[v0] = 0 # 初始点到自己的距离自然为0visited = [] # 记录已经遍历过的结点###path = dict((i, []) for i in self.G.keys()) # 初始化一个路径表,这个表记录着起始结点到途中各个点的最短路径path[v0] = str(v0) # 初始点到自己的路径自然为自己###while len(self.G) > len(visited): # 图的结点还没被遍历完时执行循环以继续遍历visited.append(current_node) # 当前点正在被遍历,所以把当前点放入visited表中for k in self.G[current_node]: # 遍历当前点的所有相邻点if dis[current_node] + self.G[current_node][k] < dis[k]: # 如果(起始点到当前点的相邻点k的距离)大于(起始点到当前点的距离+当前点到相邻点k的距离)dis[k] = dis[current_node] + self.G[current_node][k] # 则(起始点到当前点的相邻点k的距离)更新为(起始点到当前点的距离+当前点到相邻点k的距离)seq = (path[current_node], str(k))sym = '-'path[k] = sym.join(seq) # 起始点到(当前点的相邻点k)的最短路径,以'-'来连接seq中的两个字符串# 接着来选下一个当前点(current_node)# 从剩下未遍历的点中,选取与当前点的距离最小的那个点作为下一个当前点new = INFfor node in dis.keys():if node in visited: continueif dis[node] < new:new = dis[node]current_node = nodereturn dis, path# 根据本文上述定义的Path递归求路径def start_end_Path(self, Path, start, endnode, path):if start == endnode:path.append(start)else:path.append(endnode)self.start_end_Path(Path, start, Path[endnode], path)return path# 定义DirectedGraph类
class DirectedGraph(object):# 初始化def __init__(self, d, startnodelist, endnodelist):if isinstance(d, dict):self.__graph = delse:self.__graph = dict()print('数据读取错误!请查看数据格式是否正确。')# 起点列表self.startnodelist = startnodelistself.endnodelist = endnodelist# 打车费用(增加附加功能优化方案)def taxi_fare(self, distance, wait_time0):# 总里程小于19if distance < 19:wait_time = (wait_time0 * r.randint(1, 60)) / 300# 空间距离费用disfee = 0waitfee = 0if 0 <= distance <= 3:disfee += 13 + 1elif 3 < distance <= 10:disfee += 13 + 2.3 * (distance - 3) + 1elif distance > 10:disfee += 13 + 2.3 * (10 - 3) + (distance - 10) * 3.2 + 1# 等待时长换算成等效里程费用equivalent_mileage = wait_timeif 1 <= equivalent_mileage <= 3:waitfee += 13elif 3 < equivalent_mileage <= 10:waitfee += 13 + 2.3 * (equivalent_mileage - 3)elif equivalent_mileage > 10:waitfee += 13 + 2.3 * (10 - 3) + (equivalent_mileage - 10) * 3.2# 总里程大于19elif distance > 19:disfee = 0waitfee = 0# 总里程大于19小于30if distance < 30:disfee, waitfee = self.taxi_fare(15, wait_time0)extr_disfee, extr_waitfee = self.taxi_fare(distance - 15, wait_time0)disfee, waitfee = disfee + extr_disfee, (waitfee + extr_waitfee) / 2# 总里程大于30小于60elif 30 <= distance < 60:# 三目运算操作,使代码更加简洁disfee = 68 + ((distance - 30) / 30) * 79 if self.taxi_fare(15, wait_time0)[1] < 20 else 72 + ((distance - 30) / 30) * 83waitfee = self.taxi_fare(15, wait_time0)[1]# 总里程大于60elif distance >= 60:# 三目运算操作,使代码更加简洁disfee = 136 + ((distance - 60) / 60) * 169 if self.taxi_fare(15, wait_time0)[1] < 40 else 152 + ((distance - 60) / 60) * 191waitfee = self.taxi_fare(15, wait_time0)[1]return [disfee, waitfee]def timecost(self, pathoutput):redlightnumber = 0 # 红绿灯个数for i in range(len(pathoutput) - 1):redlightnumber += self.tdf.loc[pathoutput[i], pathoutput[i + 1]]timewait = 0for i in range(int(redlightnumber)):red = r.randint(0, 1)timewait += red * r.randint(1, 60)return timewait / 60# dijkstra算法实现,有向图和路由的源点作为函数的输入,最短路径最为输出def dijkstra(self, graph, startlist, endlist):lenghthoutput = {}pathoutput = {}output = {}G = Graph(graph, startlist, endlist)for start in startlist:dis, path = G.Dijkstra(start)for end in endlist:output.update({f'{start}->{end}': f'最短路径长度为:{dis[end]:.2f}km\n最短路径为:{path[end]}'})lenghthoutput.update({f'{start}-{end}': dis[end]})pathoutput.update({f'{start}-{end}': path[end]})return lenghthoutput, pathoutput, output# 获取权矩阵和时间权重矩阵def get_WTDF(self):data = self.__graphdf = pd.DataFrame(data).Tindexlist = df.index.tolist()columnslist = df.columns.tolist()self.weight_edge_list = []wdf = pd.DataFrame(index=indexlist, columns=indexlist)tdf = pd.DataFrame(index=indexlist, columns=indexlist)for i in indexlist:for j in indexlist:try:wdf.loc[i, j] = df.loc[i, j][0]tdf.loc[i, j] = df.loc[i, j][1]except:passfor i in range(len(indexlist)):for j in range(len(columnslist)):if i == j:wdf.iloc[i, j] = 0tdf.iloc[i, j] = 0wdf, tdf = wdf.replace(np.nan, float('inf')), tdf.replace(np.nan, float('inf'))for i in indexlist:for j in indexlist:if wdf.loc[i, j] != 0 and wdf.loc[i, j] != float('inf'):self.weight_edge_list.append((i, j, wdf.loc[i, j]))return wdf, tdf# 获取最短路径def get_shortestpath(self):wdf, self.tdf = self.get_WTDF()w = wdf.T.to_dict()lengthoutput, pathoutput, outputdict = self.dijkstra(w, self.startnodelist, self.endnodelist)return lengthoutput, pathoutput, outputdict# 绘制网络——可视化展现,生成路网异构图def network_graph(self, weight_edge_list, shortest_path):# 忽略除以0的报错np.seterr(divide='ignore', invalid='ignore')# 用来正常显示中文plt.rcParams['font.sans-serif'] = ['SimHei']# 用来正常显示负号plt.rcParams['axes.unicode_minus'] = FalseG2 = nx.DiGraph() # 创建:空的 有向图G2.add_weighted_edges_from(weight_edge_list) # 添加 带权边,weight表示边权# 添加 带权边,weight表示边权pos = nx.spring_layout(G2) # 用 FR算法排列节点nx.draw(G2, pos, with_labels=True, alpha=0.5)labels = nx.get_edge_attributes(G2, 'weight')nx.draw_networkx_edge_labels(G2, pos, edge_labels=labels)edgeList = []for i in range(len(shortest_path) - 1):edgeList.append((shortest_path[i], shortest_path[i + 1]))nx.draw_networkx_edges(G2, pos, edgelist=edgeList, edge_color='m', width=4) # 设置边的颜色plt.show()# 图形界面类模块
class GraphicalInterface(object):# 初始化函数def __init__(self, graph, start, end):# 创建记录数据的文件夹self.record_txt = '输入记录.txt'# 实例化Shortest_path_pro类对象self.short = DirectedGraph(graph, start, end)# 创建tk窗口self.tk = Tk()self.tk.title('考虑红绿灯的北京市道路网上出租车导航及计费')self.tk.geometry('500x500')# 输入框1self.now_nub1 = Label(self.tk, text='1、请输入起点:')self.now_nub1.grid(row=1, column=1, sticky='E')self.now_bok1 = Spinbox(self.tk, values=['交大东门', '交大南门', '交大西门'], width=25)self.now_bok1.grid(row=1, column=2, sticky='NW')# 输入框2self.now_nub2 = Label(self.tk, text='2、请输入终点:')self.now_nub2.grid(row=2, column=1, sticky='E')self.now_bok2 = Spinbox(self.tk, values=['中国农业科学院南门', '北理工北门', '海淀公园东门', '颐和园新建宫门', '北京南站进站口', '首都机场3号航站楼'],width=25)self.now_bok2.grid(row=2, column=2, sticky='NW')# 输出结果self.Output_results = Label(self.tk, text='输出结果:')self.Output_results.grid(row=8, column=1, sticky='NW')self.result_data_Text = Text(self.tk, width=40, height=30)self.result_data_Text.grid(row=10, column=2, rowspan=15, columnspan=10)self.main()# 图形界面形成def graphicalInterface(self):strs = "-" * 20start = self.now_bok1.get()end = self.now_bok2.get()# 由self.short对象获取最短路径及最短路径长度[length, pathoutput, output] = self.short.get_shortestpath()length = length[f'{start}-{end}']pathoutput = pathoutput[f'{start}-{end}'].split('-')output = output[f'{start}->{end}']# 费用构成disfee, waitfee = self.short.taxi_fare(length, self.short.timecost(pathoutput))# 获取当前电脑时间(格式化后的时间:××××-××-××)times = datetime.datetime.now().strftime('%Y-%m-%d')# 形成文案,使用字符串格式化操作text = f"{strs}记录时间{times}{strs}\n{strs}{self.now_bok1.get()}->{self.now_bok2.get()}{strs}\n{output}\n等待时间为:{self.short.timecost(pathoutput):.2f}min\n打车费用为:{disfee + waitfee:.2f}元\n费用构成分别为:空间里程收费{disfee:.2f}元和等待时长收费{waitfee:.2f}元\n{strs}{strs}\n"print(text)self.result_data_Text = Label(self.tk, text=text)self.result_data_Text.grid(row=10, column=2, rowspan=15, columnspan=3)self.short.network_graph(self.short.weight_edge_list, pathoutput)# 追加写如文件,记录操作with open(self.record_txt, 'a+', encoding='utf-8') as f:f.write(text)# 主程序(点击操作)def main(self):AnNiu = Button(self.tk, text='形成线网可视化图', fg='blue', bd=3, width=20, command=self.graphicalInterface)AnNiu.grid(row=5, column=2, sticky='NW')self.tk.mainloop()# 脚本自调试
if __name__ == '__main__':# 有向图数据文件路径filename = 'try.txt'# 输入有向图节点中起点和终点,填入列表中start_node = ['交大东门', '交大南门', '交大西门']end_node = ['中国农业科学院南门', '北理工北门', '海淀公园东门', '颐和园新建宫门', '北京南站进站口', '首都机场3号航站楼'] # 终点# 打开文件with open(filename, 'r', encoding='utf-8') as f:# 文件读取出来以后是字符数据类型,需要使用eval()方法将其本意裸露出来——字典dicts = eval(f.read())# 实例化对象test = GraphicalInterface(dicts, start_node, end_node)
可视化运行效果展示
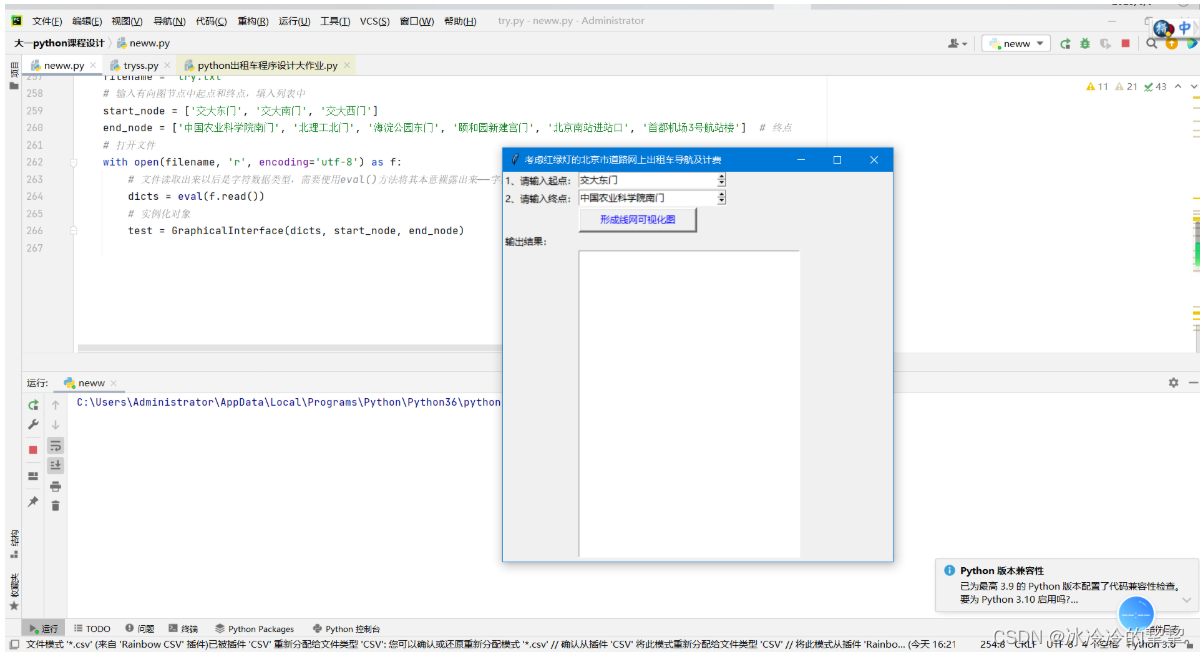
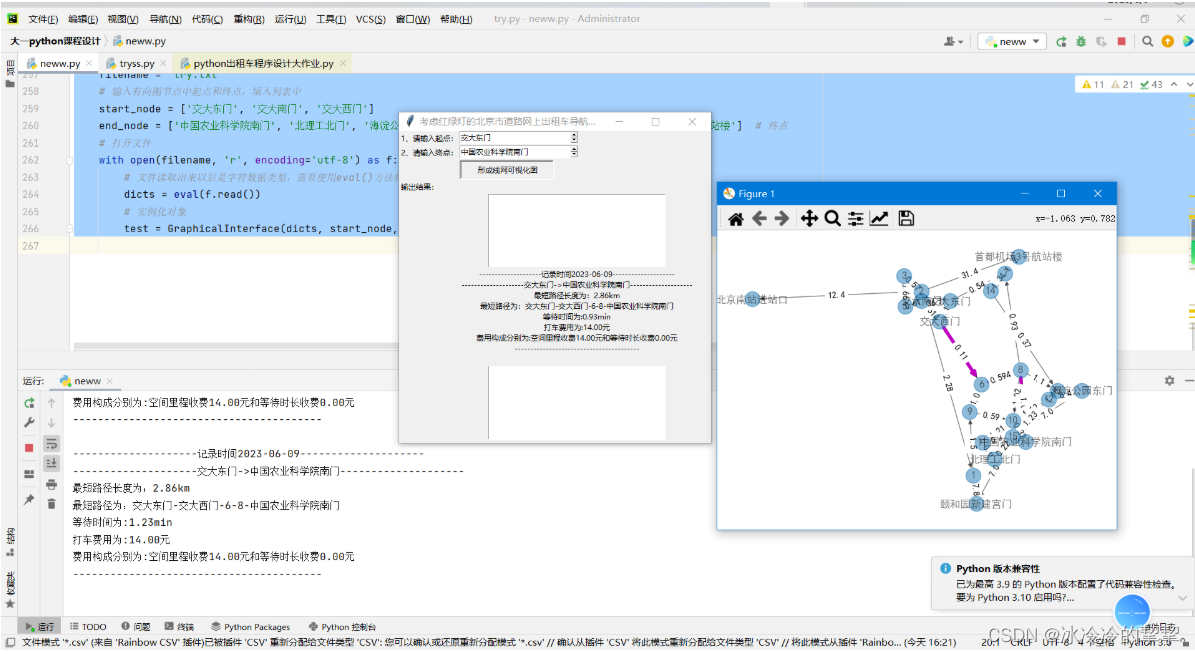
查询结果会记录在“输出记录.txt”文本文件当中。
六、总结体会感悟
总的来说,这样一份大作业让我感到十分繁琐,费了不少时间。对大一的小朋友们当中有很大难度,程序当中也没思考过多细节,可能有些过程冗余,非常欢迎大佬批评指正,笔者会虚心接受。如果有需要笔者帮助的北交的小朋友们,欢迎来找我!如果需要数据的化,关注私聊我,我可以把之前找的数据(已经用过的)给我的关注者!
这篇关于北京交通大学Python课程设计大作业(一)——考虑红绿灯的北京市道路网上出租车导航及计费的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



