纠删码ReedSolomon

本文主要是介绍纠删码ReedSolomon，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

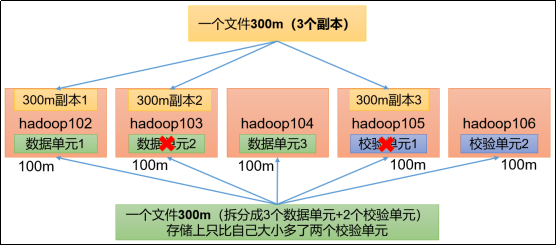
• 随着大数据技术的发展，HDFS作为Hadoop的核心模块之一得到了广泛的应用。为了数据的可靠性，HDFS通过多副本机制来保证。在HDFS中的每一份数据都有两个副本，1TB的原始数据需要占用3TB的磁盘空间，存储利用率只有1/3。
• 而且系统中大部分是使用频率非常低的冷数据，却和热数据一样存储3个副本，给存储空间和网络带宽带来了很大的压力。因此，在保证可靠性的前提下如何提高存储利用率已成为当前HDFS面对的主要问题之一。
• Hadoop 3.0 引入了纠删码技术（Erasure Coding），它可以提高50%以上的存储利用率，并且保证数据的可靠性。
• 纠删码是采用计算的方法来维持数据的一致性，并用解方程的方法对数据进行恢复，容忍一定的误差。

概念

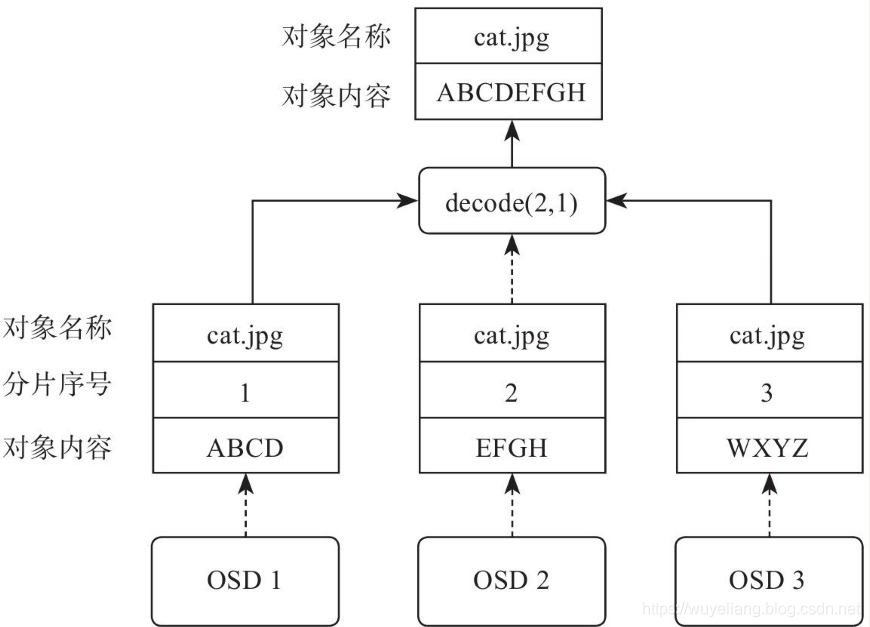
Reed-Solomon（RS）码是存储系统较为常用的一种纠删码，它有两个参数k和m，记为RS(k，m)。如下图所示，k个数据块组成一个向量被乘上一个生成矩阵（Generator Matrix）GT从而得到一个码字（codeword）向量，该向量由k个数据块和m个校验块构成。如果一个数据块丢失，可以用(GT)-1乘以码字向量来恢复出丢失的数据块。RS(k，m)最多可容忍m个块（包括数据块和校验块）丢失。

基本原理

容忍度

冗余符号的个数可以人为指定

数据的生成

把输入数据视为向量D=(D1，D2，…, Dn）, 编码后数据视为向量（D1, D2,…, Dn, C1, C2,…, Cm)，RS编码可视为如下图所示矩阵运算。

上图最左边是编码矩阵（或称为生成矩阵、分布矩阵，Distribution Matrix），编码矩阵需要 满足任意n*n子矩阵可逆。 为方便数据存储，编码矩阵上部是单位阵（n行n列），下部是m行n列矩阵。下部矩阵可以选择范德蒙德矩阵或柯西矩阵。

这里我们假设7和50丢失了 下方是恢复的过程，很简单解一个方程组就行。

7 x
50 y
x + 2*8 + 3 * 9 = y
4x + 5*8 + 6 * 9 = 122

数据的恢复

采用高斯消元的方法，我们来看一个具体的例子。

这篇关于纠删码ReedSolomon的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---