堆排序 Heapsort

本文主要是介绍堆排序 Heapsort，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

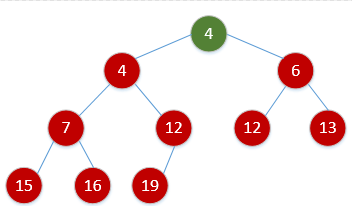
堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法：

1. 大顶堆：每个节点的值都大于或等于其子节点的值，在堆排序算法中用于升序排列；
2. 小顶堆：每个节点的值都小于或等于其子节点的值，在堆排序算法中用于降序排列；

堆排序的平均时间复杂度为 Ο(nlogn)。

动态演示 :

分析 :

这里给个视频理解堆排序 :选择排序_堆排序_1什么是堆排序_哔哩哔哩_bilibili

代码 :

    public static void main(String[] args) {int[] arr = {10, 78, 65, 32, 21, 89, 13, 54, 7, 3};HeapSort(arr);}//堆排序public static void HeapSort(int[] nums) {int[] arr = Arrays.copyOf(nums, nums.length);int len = arr.length;//构建堆buildMaxHeap(arr, len);for (int i = len - 1; i > 0; i--) {swap(arr,0,i);len--;heapify(arr,0,len);}System.out.println(Arrays.toString(arr));}//构建堆public static void buildMaxHeap(int[] arr, int len) {for (int i = len >> 1; i >= 0; i--) {heapify(arr, i, len);}}private static void heapify(int[] arr, int i, int len) {int left = 2 * i + 1;int right = 2 * i + 2;int largest = i;if (left < len && arr[left] > arr[largest]) {largest = left;}if (right < len && arr[right] > arr[largest]) {largest = right;}if (largest != i) {swap(arr, i, largest);heapify(arr, largest, len);}}//交换public static void swap(int[] arr, int i, int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}

这篇关于堆排序 Heapsort的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---