“帆软杯”武汉大学2022级新生程序设计竞赛

好差劲 打的最差的一场比赛

参考官方题解及“帆软杯”武汉大学2022级新生程序设计竞赛 (更新至8题) - 知乎 (zhihu.com)

先补这么多。

目录

比赛链接：

B 苹果排序

D 甩锅

F 最短公共超串

H 犹太棋（Easy Version)

I 犹太棋（Hard Version)

L 最大公约数

M WHU

比赛链接

“帆软杯”武汉大学2022级新生程序设计竞赛

B 苹果排序

        上一篇题解里提到说，逆序对个数等于冒泡排序的交换次数（使数列有序的最小相邻交换次数）。
        已知交换位置差为奇数代价为1，偶数为-1，则进行x次相邻交换的代价就为x。假设把原数组排列成有序需要x次交换，那当前代价就是x，现在需要-x的代价与它抵消。
        如果交换过来又交换回去，原数组不变，但是次数需要偶数次，所以如果逆序对是偶数次，就可以使得代价为0，如果逆序对是奇数次，就无法使得代价为0

#include <iostream>
using namespace std;
const int N = 2e5 + 10;
int a[N];
int c[N];
int n;
int lowbit(int x)
{return (x & -x);
}
void add(int x, int v)
{for(; x <= n; x += lowbit(x))c[x] += v;
}
int query(int x)
{long long ans = 0;for(;x; x -= lowbit(x))ans += c[x];return ans;
}
void solve()
{cin >> n;for(int i = 1; i <= n; ++ i){cin >> a[i];c[i] = 0;}long long ans = 0;for(int i = n; i >= 1; -- i){add(a[i], 1);ans += query(a[i - 1]);}if(ans % 2 == 0) cout << "YES" << endl;else cout << "NO" << endl;
}
int main()
{int t;cin >> t;while( t -- )solve();
}

D 甩锅

比较他们的数学期望即可。

A的数学期望为 ，B的数学期望为。

#include <iostream>
using namespace std;
void solve()
{long long x, a, y, b;cin >> x >> a >> y >> b ;if((a + 1) * x == ( b + 1) * y) cout << "YES" << endl;else cout << "NO" << endl;
}
int main()
{int t;cin >> t;while( t -- )solve();
}

F 最短公共超串

我们贪心地可以发现只有两种情况，b接在a的后面或者b接在a的后面。答案就是去掉他们中间重复部分之后的字符串。

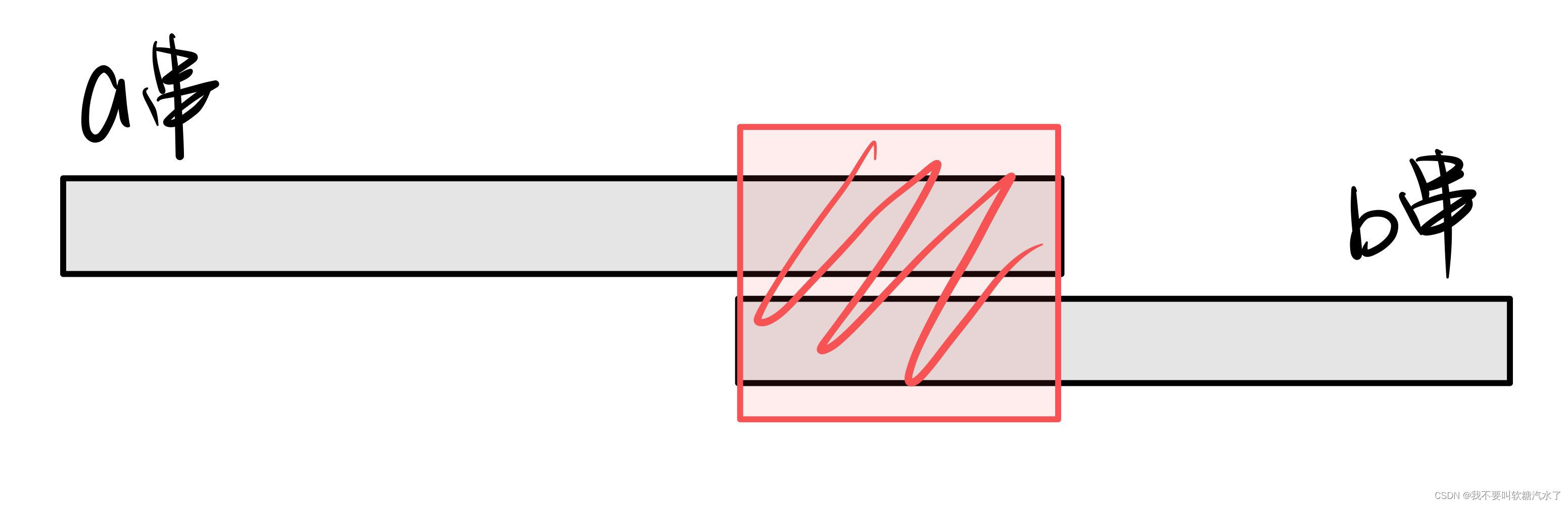
我们可以发现，如果把b串放在a串前面，那这个公共部分就会被拆成这样。

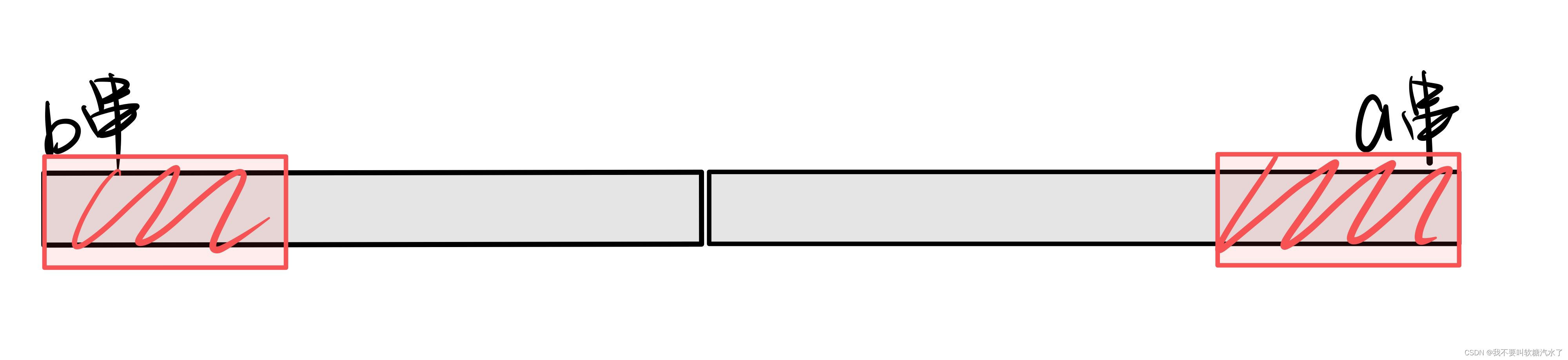
由于这个部分的字符串完全相等，这样可以很明显看出这个公共部分其实就是字符串b+a的公共前后缀。对于b接在a后面的情况也是同理，只要求字符串a+b的公共前后缀就是他们的重合部分，也是就要求ne[ ]数组。

除此之外，有可能这个公共前后缀特别的长，甚至大于b串的长度或者a串的长度，很明显这是不合法的，拼接回来之后并不能成为他们的重合部分。对于这样的情况，我们只要再继续求这个部分的公共前后缀，直到ne[ ]数组小于n和m。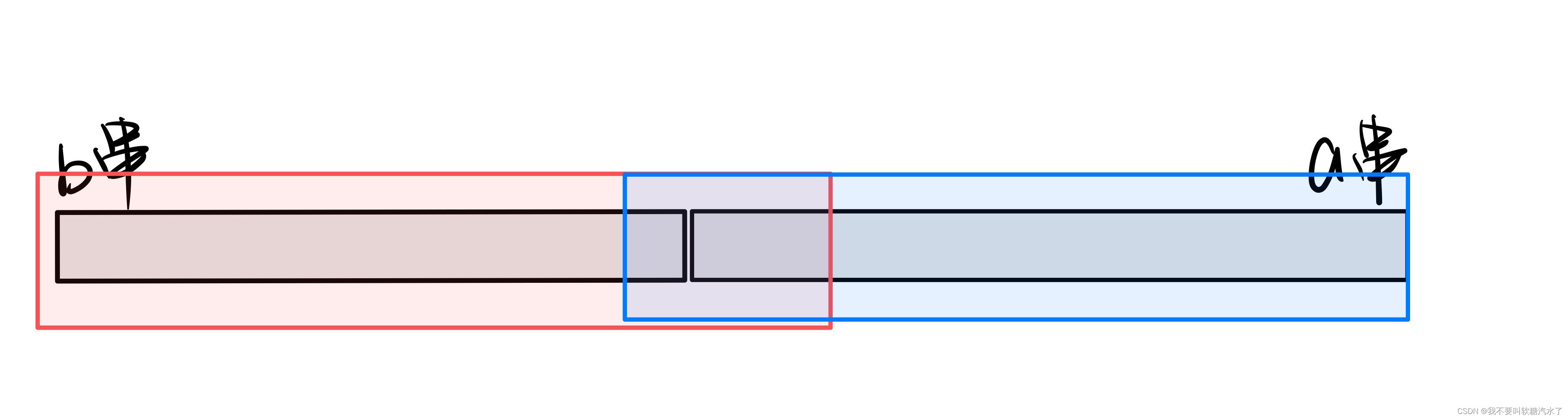

#include <bits/stdc++.h>
#define endl '\n'
#define mk make_pair
using namespace std;
typedef pair<int,int> PII;
const int INF = 0x3f3f3f3f;
const int N = 4e5 + 10;
char a[N], b[N];
int ne1[N];
int ne2[N];
int main() 
{ios::sync_with_stdio(false);cin.tie(0);cin >> (a + 1) >> (b + 1);int n, m;n = strlen(a + 1), m = strlen(b + 1);string sa, sb;for(int i = 1; i <= n; ++ i)sa += a[i];for(int i = 1; i <= m; ++ i)sb += b[i];if(~sa.find(sb))cout << sa << endl;else if(~sb.find(sa))cout << sb << endl;else{for(int i = n + 1; i <= n + m; i ++ )a[i] += b[i - n];for(int i = 2, j = 0 ; i <= n + m; ++ i){while(j && a[i] != a[j + 1])j = ne1[j];if(a[i] == a[j + 1]) j ++ ;ne1[i] = j;}string s1;int t = ne1[n + m];while( t > min(n, m)) t = ne1[t];for(int i = 1; i <= m; ++ i)s1 += b[i];for(int i = t + 1; i <= n; ++ i)s1 += a[i];for(int i = m + 1; i <= n + m; ++ i)b[i] = a[i - m];for(int i = 2, j = 0; i <= n + m; ++ i){while( j && b[i] != b[j + 1] ) j = ne2[j];if(b[i] == b[j + 1]) j ++;ne2[i] = j;}string s2;t = ne2[n + m];while( t > min(n, m)) t = ne2[t];for(int i = 1; i <= n; ++ i)s2 += a[i];for(int i = t + 1; i <= m; ++ i)s2 += b[i];if(s1.size() < s2.size())cout << s1 << endl;elsecout << s2 << endl;}return 0;
}

H 犹太棋（Easy Version)

这题我觉得官方题解说得特别清楚。

        输出”YES” 即可通过本题目。 若棋盘数目是奇数，先手方在 （1+n) / 2 处放一个棋子，将棋盘分成相同长度 的两份，对方在一边怎么拿，就在另一边复制他的下法，这样先手方肯定 能拿走最后一颗棋子并获胜。

        若棋盘数目是偶数，先手方拿走中间两颗即可。 

I 犹太棋（Hard Version)

利用sg函数即可，把原始棋子分成的很多段棋盘看成是很多不同局面的游戏，然后取异或和。

在sg函数里枚举在棋盘中间放1~3颗棋子的后续局面。

#include <bits/stdc++.h>
#define endl '\n'
#define mk make_pair
using namespace std;
typedef pair<int,int> PII;
const int INF = 0x3f3f3f3f;
const int N = 3e3 + 10;
int f[N];
int n;
int sg(int x)
{if(f[x] != -1) return f[x];unordered_set<int>S;for(int j = 1; j <= x; ++ j)//当前局面的所有子局面{S.insert(sg(j - 1) ^ sg(x - j));if(j >= 2) S.insert(sg(j - 2) ^ sg(x - j));if(j >= 3) S.insert(sg(j - 3) ^ sg(x - j));}for(int i = 0;; i ++){if(!S.count(i)){f[x] = i;return f[x];}}
}
int main() 
{ios::sync_with_stdio(false);cin.tie(0);memset(f, -1 , sizeof f);f[0] = 0;cin >> n;string s;cin >> s;s = "1" + s;int last = 0;vector<int>vec;for(int i = 1; i <= n; ++ i){if(s[i] == '1'){if(i - last - 1)vec.push_back(i - last - 1);last = i;}}if( n - last) vec.push_back(n - last);f[0] = 0;int res = 0;for(auto x : vec)res ^= sg(x);if(res) cout << "YES" << endl;else cout << "NO" << endl;return 0;
}

L 最大公约数

由于，每次减去与前面答案里的gcd的个数后，当前数组里最大的那个数一定是原数组里的元素。

#include <bits/stdc++.h>
#define endl '\n'
#define mk make_pair
using namespace std;
typedef pair<int,int> PII;
const int INF = 0x3f3f3f3f;
const int N = 1e6 + 10;
int a[N];
int ans[N];
int gcd(int a, int b)
{return a % b == 0 ? b : gcd(b, a % b);
}
bool cmp(int a, int b)
{return a > b;
}
int main() 
{ios::sync_with_stdio(false);cin.tie(0);map<int, int>cnt;int n;cin >> n;for(int i = 1; i <= n * n ; ++ i){cin >> a[i];cnt[a[i]] ++;}sort(a + 1 , a + (n * n + 1), cmp);int k = 0;for(int i = 1; i <= n * n; ++ i){if(cnt[a[i]] <= 0) continue;for(int j = 1; j <= k; ++ j){int t = gcd(a[i], ans[j]);cnt[t] -= 2;}if(cnt[a[i]] <= 0) continue;ans[ ++ k] = a[i];if( k == n ) break;}for(int i = n; i >= 1; -- i)cout << ans[i] << " \n"[i == 1];return 0;
}

M WHU

深搜即可

#include <iostream>
#include <cstring>
using namespace std;
int g[30][30];
int h[30], e[30], ne[30], idx;
int ans = 0;
void add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs(int u)
{if(u == 12){ans ++;return;}for(int i = h[u]; ~i; i = ne[i]){int j = e[i];dfs(j);}
}
int main()
{
//     int n, m;
//     cin >> n >> m;
//     memset(h, -1, sizeof h);
//     while( m -- )
//     {
//         int a, b;
//         cin >> a >> b;
//         add(a, b);
//     }//     dfs(1);
//     cout << ans << endl;cout << 14 << endl;
}