本文主要是介绍左神算法:找到二叉树中符合搜索二叉树条件的最大拓扑结构(Java版),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本题来自左神《程序员代码面试指南》“找到二叉树中符合搜索二叉树条件的最大拓扑结构”题目。
题目
牛客OJ:找到二叉树中符合搜索二叉树条件的最大拓扑结构
给定一棵二叉树的头节点head,已知所有节点的值都不一样,返回其中最大的且符合搜索二叉树条件的最大拓扑结构的大小。
例如,二叉树如图 3-19 所示。

其中最大的且符合搜索二叉树条件的拓扑结构如图3-20 所示。
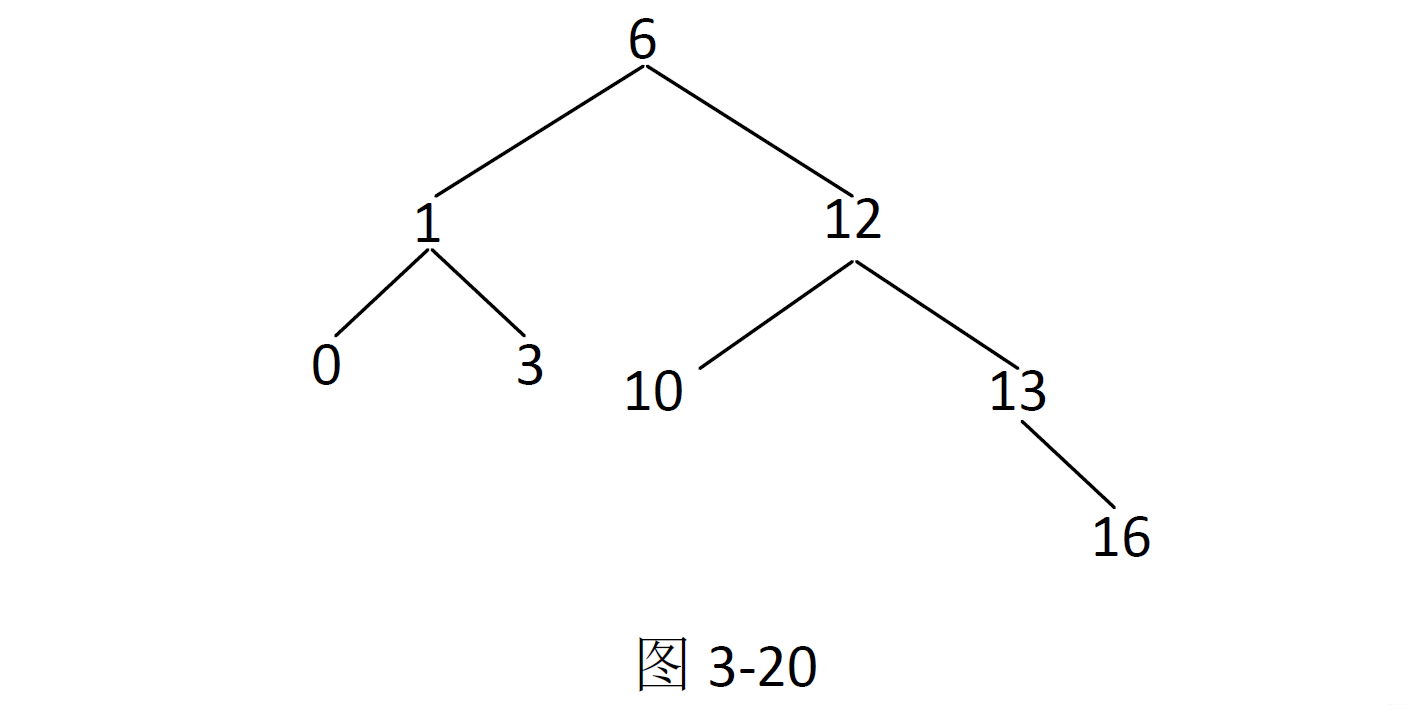
这个拓扑结构节点数为8,所以返回8。
题解
方法一:二叉树的节点数为N,时间复杂度为O(N^2)的方法。
首先来看这样一个问题,以节点 h 为头节点的树中,在拓扑结构中也必须以 h 为头节点的情况下,怎么找到符合搜索二叉树条件的最大结构?
这个问题有一种比较容易理解的解法,我们先考查 h 的孩子节点,根据孩子节点的值从 h 开始按照二叉搜索的方式移动,如果最后能移动到同一个孩子节点上,说明这个孩子节点可以作为这个拓扑的一部分,并继续考查这个孩子节点的孩子节点,一直延伸下去。
只要遍历所有的二叉树节点,并在以每个节点为头节点的子树中都求一遍其中的最大拓扑结构,其中最大的那个就是我们想找的结构,它的大小就是返回值。
具体过程请参看下面代码中的 bstTopoSize1 方法。
对于方法一的时间复杂度分析,我们把所有的子树(N 个)都找了一次最大拓扑,每找一次,所考查的节点数都可能是O(N)个节点,所以方法一的时间复杂度为O(N2)。
方法二:二叉树的节点数为N,时间复杂度为O(N)的方法。
先来说明一个对方法二来讲非常重要的概念——拓扑贡献记录。还是举例说明,请注意题目中以节点10 为头节点的子树,这棵子树本身就是一棵搜索二叉树,那么整棵子树都可以作为以节点10 为头节点的符合搜索二叉树条件的拓扑结构。如果对如图3-19 所示的拓扑结构建立贡献记录,则是如图3-21 所示的样子。
在图3-21 中,每个节点的旁边都有被括号括起来的两个值,我们把它称为节点对当前头节点的拓扑贡献记录。第一个值代表节点的左子树可以为当前头节点的拓扑贡献几个节点,第二个值代表节点的右子树可以为当前头节点的拓扑贡献几个节点。比如,4(1,1)括号中的第一个1代表节点4 的左子树可以为节点10 为头的拓扑结构贡献1 个节点,第二个1 代表节点4 的右子树可以为节点10 为头节点的拓扑结构贡献1 个节点。同样,我们也可以建立以节点13 为头节点的记录,如图3-22 所示。
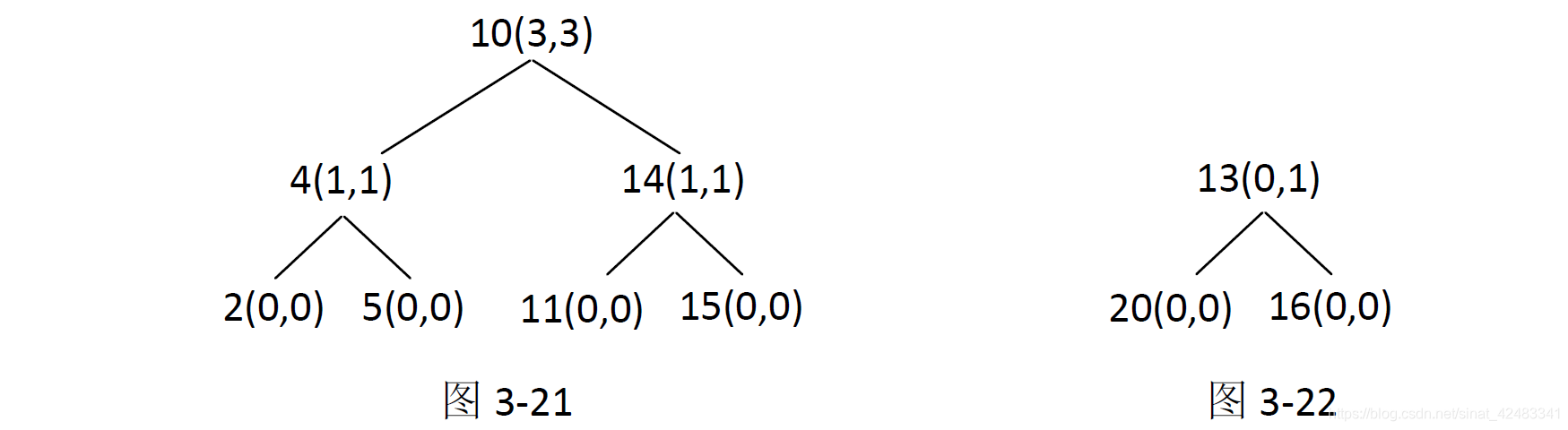
整个方法二的核心就是如果分别得到了 h 左右两个孩子节点为头节点的拓扑贡献记录,可以快速得到以 h 为头节点的拓扑贡献记录。
整个过程大体说来是利用二叉树的后序遍历,对每个节点来说,首先生成其左孩子节点的记录,然后是右孩子节点的记录,接着把两组记录修改成以这个节点为头的拓扑贡献记录,并找出所有节点的最大拓扑结构中最大的那个。
方法二的全部过程,请参看如下代码中的 bstTopoSize2 方法。
代码
package chapter_3_binarytreeproblem;import java.util.HashMap;
import java.util.Map;// 找到二叉树中符合搜索二叉树条件的最大拓扑结构
public class Problem_08_BiggestBSTTopologyInTree {public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}}/*** 方法一:时间复杂度 O(n^2)* 只要遍历所有的二叉树节点,并在以每个节点为头节点的子树中都求一遍其中的最大拓扑结构,* 其中最大的那个就是我们想找的结构,它的大小就是返回值。*/public static int bstTopoSize1(Node head) {if (head == null) {return 0;}int max = maxTopo(head, head); // 在以head为头结点的树中,在拓扑结构也以h为头结点的情况下,找最大拓扑max = Math.max(bstTopoSize1(head.left), max); // 遍历其左子树max = Math.max(bstTopoSize1(head.right), max); // 遍历其右子树return max;}/*** 在以h为头结点的树中,在拓扑结构以n为头结点的情况下,找最大拓扑** @param h 整棵树的头结点* @param n 拓扑结构的头结点* @return 最大拓扑包含的节点数量*/public static int maxTopo(Node h, Node n) {// 先考查h的孩子节点,调用isBSTNode考察这个孩子节点是否可以作为这个(以h为头结点的)拓扑的一部分。// 如果可以,则继续考查这个孩子节点的孩子节点,一直延伸下去。if (h != null && n != null && isBSTNode(h, n)) {// 最大拓扑结构包含节点数量 = n的左子树的最大拓扑数量 + n的右子树的最大拓扑数量 + n本身return maxTopo(h, n.left) + maxTopo(h, n.right) + 1;}return 0; // 当前节点不能作为整个拓扑的一部分延伸下去,故返回0}// 在以h为头结点的树中,用二叉搜索的方式能否找到节点npublic static boolean isBSTNode(Node h, Node n) {if (h == null) {return false;}if (h == n) {return true;}return isBSTNode(h.value > n.value ? h.left : h.right, n); // 标准的BST递归过程。根据比较大小,在h的左子树或右子树中查找节点n。}/*** 以下为方法二*/public static class Record {public int l; // 节点的左子树可以为当前头结点的拓扑贡献几个节点public int r; // 节点的右子树可以为当前头结点的拓扑贡献几个节点public Record(int left, int right) {this.l = left;this.r = right;}}/*** 方法二:找到二叉树中符合搜索二叉树条件的最大拓扑结构*/public static int bstTopoSize2(Node head) {Map<Node, Record> map = new HashMap<Node, Record>(); // <节点,以这个节点为头的拓扑贡献记录>return posOrder(head, map);}/*** 整个过程大体说来是利用二叉树的后序遍历,对每个节点来说,首先生成其左孩子节点的记录,然后是右孩子节点的记录,* 接着把两组记录修改成以这个节点为头的拓扑贡献记录,并找出所有节点的最大拓扑结构中最大的那个。** @param h* @param map* @return*/public static int posOrder(Node h, Map<Node, Record> map) {if (h == null) {return 0;}int ls = posOrder(h.left, map); // 后序遍历左子树int rs = posOrder(h.right, map); // 后序遍历右子树// 计算并处理当前节点modifyMap(h.left, h.value, map, true); // 生成其左孩子节点的记录modifyMap(h.right, h.value, map, false); // 生成其右孩子节点的记录Record lRecord = map.get(h.left); // 拿到左孩子的记录Record rRecord = map.get(h.right); // 拿到右孩子的记录int lBST = (lRecord == null ? 0 : lRecord.l + lRecord.r + 1); // 计算左孩子为头的拓扑贡献记录(为生成当前节点的记录做准备)int rBST = (rRecord == null ? 0 : rRecord.l + rRecord.r + 1); // 计算右孩子为头的拓扑贡献记录(为生成当前节点的记录做准备)map.put(h, new Record(lBST, rBST)); // 生成当前节点为头的拓扑贡献记录return Math.max(lBST + rBST + 1, Math.max(ls, rs)); // 判断以当前节点为头、以左/右孩子为头,二者哪个更大,找出所有节点的最大拓扑结构中最大的那个}/*** 处理以headValue节点为头的拓扑贡献记录,并更新到map中** @param node 需要判断的节点(是v的左孩子或右孩子)* @param headValue BST头结点的值* @param map 记录表* @param isLChild 是否是左孩子* @return 总共删掉的节点个数*/public static int modifyMap(Node node, int headValue, Map<Node, Record> map, boolean isLChild) {if (node == null || (!map.containsKey(node))) {return 0;}Record record = map.get(node); // 拿到node节点的旧记录record// n是左孩子且比头结点的值大,或n是右孩子且比头结点的值小,说明不满足BST,故删除if ((isLChild && node.value > headValue) || ((!isLChild) && node.value < headValue)) {map.remove(node);return record.l + record.r + 1; // 返回总共删掉的节点数} else { // n满足BSTint minus = modifyMap(isLChild ? node.right : node.left, headValue, map, isLChild); // 如果是左子树,则递归其右边界;如果是右子树,则递归其左边界if (isLChild) { // 如果node本身是左子树,则其右子树的贡献记录被更新record.r = record.r - minus;} else { // 如果node本身是右子树,则其左子树的贡献记录被更新record.l = record.l - minus;}// 将更新后的node的记录同步到map中map.put(node, record);return minus;}}// for test -- print treepublic static void printTree(Node head) {System.out.println("Binary Tree:");printInOrder(head, 0, "H", 17);System.out.println();}public static void printInOrder(Node head, int height, String to, int len) {if (head == null) {return;}printInOrder(head.right, height + 1, "v", len);String val = to + head.value + to;int lenM = val.length();int lenL = (len - lenM) / 2;int lenR = len - lenM - lenL;val = getSpace(lenL) + val + getSpace(lenR);System.out.println(getSpace(height * len) + val);printInOrder(head.left, height + 1, "^", len);}public static String getSpace(int num) {String space = " ";StringBuffer buf = new StringBuffer("");for (int i = 0; i < num; i++) {buf.append(space);}return buf.toString();}public static void main(String[] args) {Node head = new Node(6);head.left = new Node(1);head.left.left = new Node(0);head.left.right = new Node(3);head.right = new Node(12);head.right.left = new Node(10);head.right.left.left = new Node(4);head.right.left.left.left = new Node(2);head.right.left.left.right = new Node(5);head.right.left.right = new Node(14);head.right.left.right.left = new Node(11);head.right.left.right.right = new Node(15);head.right.right = new Node(13);head.right.right.left = new Node(20);head.right.right.right = new Node(16);printTree(head);System.out.println(bstTopoSize1(head));System.out.println(bstTopoSize2(head));}
}
这篇关于左神算法:找到二叉树中符合搜索二叉树条件的最大拓扑结构(Java版)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






