决策树(二)：CART回归树与Python代码

本文主要是介绍决策树(二)：CART回归树与Python代码，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

上一篇介绍了决策树的基本概念，特征划分标准及ID3､C4.5和CART分类树的算法，本文着重对CART回归树的内容进行补充。

本文概览：
首先介绍CART回归树的算法，然后是创建CART回归树的主要步骤，最后是实现该过程的Python代码。

一、CART回归树算法

CART回归树处理的是回归问题，数据集的标签不再是离散的类别值，而是一系列的连续值的集合。
CART回归树不同于线性回归模型，不是通过拟合所有的样本点来得到一个最终模型进行预测，它是一类基于局部的回归算法，通过采用一种二分递归分割的技术将数据集切分成多份，每份子数据集中的标签值分布得比较集中（比如以数据集的方差作为数据分布比较集中的指标），然后采用该数据集的平均值作为其预测值。这样，CART回归树算法也可以较好地拟合非线性数据。

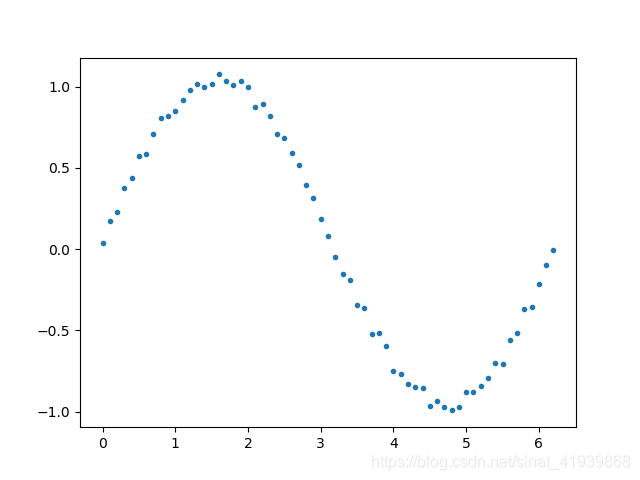
假如数据集的标签(目标值)的集合呈现如下非线性目标函数的值，CART回归树算法将数据集切分成很多份，即将如下函数切成一小段一小段的，对于每一小段的值是较为接近的，可以每一小段的平均值作为该小段的目标值。

二、CART回归树生成

1. CART回归树的划分

在CART分类树中，是利用Gini指数作为划分的指标，通过样本中的特征对样本进行划分，直到所有的叶节点中的所有样本均为一个类别为止。其中，Gini指数表示的是数据的混乱程度，对于回归树，样本标签是连续数据，当数据分布比较分散时，各个数据与平均值的差的平方和较大，方差就较大；当数据分布比较集中时，各个数据与平均值的差的平方和较小。方差越大，数据的波动越大；方差越小，数据的波动就越小。因此，对于连续的数据，可以使用样本与平均值的差的平方和作为划分回归树的指标。

假设，有m个训练样本，{(X⁽¹⁾,y⁽¹⁾),(X⁽²⁾,y⁽²⁾), …, (X^(m),y^(m))}, 则划分CART回归树的指标为：
$$m\ast s^2=\sum _{i=1}^m(y^{}$$

这篇关于决策树(二)：CART回归树与Python代码的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---