本文主要是介绍多视几何,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
多视图几何是主要研究用几何的方法,通过若干幅多视图几何二维图像,来恢复三维物体。间言之就是研究三维重构。
1.对极几何基础概念
核点(epipole):基线(baseline)与成像平面的交点。同时极点也可以理解为相邻影像成像中心在本影像上的像,因为基线是两个相邻影像成像中心的连线。
核平面(epipolar plane):含有基线的平面,是一簇平面。可以看做是由基线与空间中任意一点构成的平面。
核线(epipolar line):核平面与成像平面的交线。可以看做是成像平面上的任意一点(非核点)与核点所定义的直线。

2. 基础矩阵 F
基础矩阵可以看做是将点投影(转换)为直线,将左影像上的一个点投影到右影像上形成一条核线。
基础矩阵表示的是图像中的像点p1到另一幅图像对极线l2的映射,有如下公式:
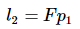
而和像点P1P1匹配的另一个像点p2必定在对极线l2上,所以就有:
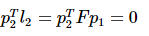
这样仅通过匹配的点对,就可以计算出两视图的基础矩阵F。
基础矩阵FF是一个3×3的矩阵,有9个未知元素,由于尺度是任意的,所以只需要8个方程。因为算法中需要8个对应点来计算基础矩阵F,所以该算法叫做八点法。
3.8点法估算基础矩阵F
由于基础矩阵 F 定义为
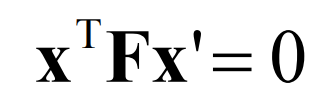
任给两幅图像中的匹配点 x 与 x’,令
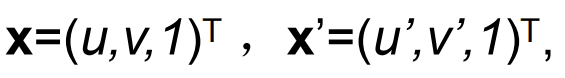
 <
<
这篇关于多视几何的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







