本文主要是介绍# [cs231n (七)神经网络 part 3 : 学习和评估 ][1],希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
cs231n (七)神经网络 part 3 : 学习和评估
标签(空格分隔): 神经网络
文章目录
- [cs231n (七)神经网络 part 3 : 学习和评估 ][1]
- 同类文章
- 0.回顾
- 1.引言
- 2. 梯度检验
- 3. 做到:合理性检查
- 4. 接下来检查整个学习过程
- 1. 损失函数
- 2. 训练和验证集精度
- 3. 权重更新
- 4. 层激活数及梯度分布情况
- 5. 参数更新
- 1. 随机梯度下降
- 2. 学习率退化
- 3. 二阶法
- 4. 逐层层自适应学习率:Adagrad、RMSprop
- 6. 超参数优化
- 7. 评估([集成模型][17])
- 8. 总结
- 9. 附录拓展
- 转载和疑问声明
- 我祝各位帅哥,和美女,你们永远十八岁,嗨嘿嘿~~~
同类文章
cs231n (一)图像分类识别讲了KNN
cs231n (二)讲了线性分类器:SVM和SoftMax
cs231n (三)优化问题及方法
cs231n (四)反向传播
cs231n (五)神经网络 part 1:构建架构
cs231n (六)神经网络 part 2:传入数据和损失
cs231n (七)神经网络 part 3 : 学习和评估
cs231n (八)神经网络总结:最小网络案例研究
cs231n (九)卷积神经网络
0.回顾
cs231n (一)图像分类识别讲了KNN
cs231n (二)讲了线性分类器:SVM和SoftMax
cs231n (三)优化问题及方法
cs231n (四)反向传播
cs231n (五)神经网络 part 1:构建架构
cs231n (六)神经网络 part 2:传入数据和损失
1.引言
之前入门了一个两层的神经网络,基本就是网络框架,现在就需要好好优化网络了,来打开电脑开干哈、、、么么哒~
2. 梯度检验
意不意外、惊不惊喜? 我有出现了、
其实这里就一点:用中心化公式更好
d f ( x ) d x = f ( x + h ) − f ( x ) h ( b a d ) \displaystyle \frac{df(x)}{dx}=\frac{f(x+h)-f(x)}{h} (bad) dxdf(x)=hf(x+h)−f(x)(bad)
按照定义h是一个趋近于零的数值,目前计算机的能力下:近似为1e-5
d f ( x ) d x = f ( x + h ) − f ( x − h ) 2 h ( i n s t e a d ) \displaystyle \frac{df(x)}{dx}=\frac{f(x+h)-f(x-h)}{2h}(instead) dxdf(x)=2hf(x+h)−f(x−h)(instead)
反正目前来说就是:费力(耗费计算能力)不讨好!
关于梯度检验我们需要掌握几点:
- 使用双精度计算会降低误差
- 保持小数的有效数值 看《电脑科学家应该知道的浮点运算》
- 目标函数不可导的时候也会影响梯度精度的
- 使用数据少点:笨啊,因为这样不可导的数据点就越少啊
- 梯度检验期间最好是不要使用正则化
- 不要使用dropout和数据增强(augmentation)
- 等待梯度开始下降后再开始梯度检查
- 检查部分维度:假设其他维度是正确的
- 步长h的设置:一般是1e-4 ----> 1e-6 为什么?
看了这张图就知道为什么了。

3. 做到:合理性检查
- 特定情况下的损失值应该合理
- 是否是因为提高了正则化强度之后导致的损失值变大
- 小数据的过拟合:不要用正则化,使用20个数据应该能达到损失是零
4. 接下来检查整个学习过程
其实就是跟踪一些重要的参数,从而达到修改超参数的便利, 比如:每个epoch的loss
1. 损失函数
损失值跟踪: 可以得到不同学习率下的损失值变化情况
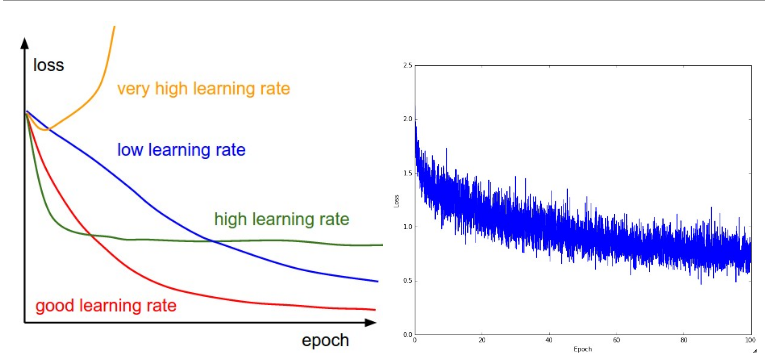
左边:不同学习率下的loss变化,右边:随着epochloss的变化
loss震荡程度和batch size有关系哦,当size=1 震荡程度就会很大,当size=N也就是整个数据,那么震荡最小
2. 训练和验证集精度
紧接着需要跟踪的另一个指标就是:验证和训练集的准确率,看下图

- 训练集和验证集之间的空隙说明:模型的过拟合程度 验证集的准确率很低,说明模型严重过拟合, 此时应该增大正则化强度(正则化项、dropout、增加数据)
- 再则就是验证曲线和训练曲线很接近,说明模型容量太小,应该增加参数数量。
3. 权重更新
最后一个指标就是:权重值更新了的数量和全部值的比
这个比例应该在1e-3左右,如果小,说明学习率小,如如果大,说明学习率太大。
# assume parameter vector W and its gradient vector dW
param_scale = np.linalg.norm(W.ravel())
update = -learning_rate*dW # simple SGD update
update_scale = np.linalg.norm(update.ravel())
W += update # the actual update
print update_scale / param_scale # want ~1e-3
4. 层激活数及梯度分布情况
初始化问题,梯度消失或者nan值,解决办法:得到网络中所有层的激活数据及梯度分布,观测数据结果, 我们看一下下面的图就知道了。
对于图像数据,我们可视化第一层特征。

左边:特征乱七八糟,网络应该是没有收敛,学习率不当,正则化权重太低
右边:特征明显,种类多,好图。
5. 参数更新
当我们使用BP计算梯度以后,梯度就可以更新了,那么如何更新呢?
1. 随机梯度下降
-
一般更新沿着负梯度调参
-
x += - learning_rate * dx比如 : α \alpha α = 0.05 -
动量更新新方法,在深度学习中总是能快速收敛
从物理角度讲,想象一座高山,高度势能是U=mgh,so: U ∝ h U\propto h U∝h
质点所受的力与梯度的能量 ( F = − ∇ U ) (F=-\nabla U) (F=−∇U)有关,**其实就是保守力就等于势能的负梯度!!!**物理专业的骄傲哈哈、
而又因为: F = m a F = ma F=ma 所以有:
# 动量法
v = mu * v - learning_rate * dx # 融合速度
x += v # 融合位置
引入参数 mu和v , 前者就是动量咯,最后结论:mu = [0.5,0.9,0.95,0.99]
要注意mu不是恒定不变的,一般是从0.5慢慢提升至0.99
- Nesterov动量 理论上更有比较好的支持,实践下比上述动量还好。
当向量位于某个位置x时,mu * v 会轻微改变参数向量,因此计算梯度时,应该计算x + mu * v就更有意义???
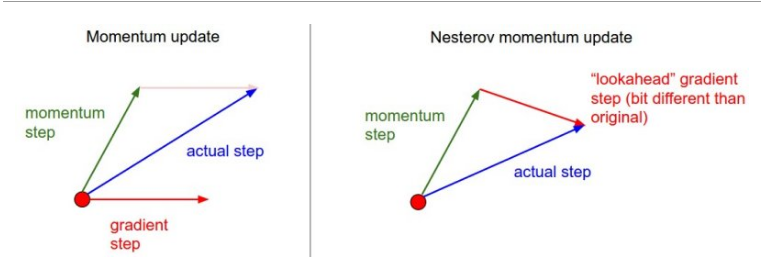
动量将会把我们带到绿色箭头的位置,那么应该再向前看一些。
就知道你听的一头雾水!
x_ahead = x + mu * v
# 计算dx_ahead(x_ahead处的梯度)
v = mu * v - learning_rate * dx_ahead
x += v
实际中改写x_ahead = x + mu * v就懂了。
x += -mu * v_prev + (1 + mu) * v && v_prev = v
x += v
v_prev = v # back this up
v = mu * v - learning_rate * dx # velocity update stays the same
x += -mu * v_prev + (1 + mu) * v # position update changes form
这是Yoshua Bengio的文献
2. 学习率退化
-
**随epoch衰减:**一般是每5个epoch减少一半,看验证集的错误率停止下降,就乘常数,降低学习率。
-
指数衰减: α = α 0 e − k t \alpha=\alpha_0e^{-kt} α=α0e−kt
-
1/t衰减: α = α 0 / ( 1 + k t ) \alpha=\alpha_0/(1+kt) α=α0/(1+kt)
α 0 \alpha_0 α0,k:超参数,t:迭代次数
随步数衰减的随机失活(dropout)更受欢迎
3. 二阶法
还有最优化方法是基于牛顿法的:
x ← x − [ H f ( x ) ] − 1 ∇ f ( x ) \displaystyle x\leftarrow x-[Hf(x)]^{-1}\nabla f(x) x←x−[Hf(x)]−1∇f(x)
其中 H f ( x ) Hf(x) Hf(x)是Hessian矩阵, 这里是没有学习率这个参数或者说概念的, 这个方法啊,少用。
4. 逐层层自适应学习率:Adagrad、RMSprop
Adagrad:一个由Duchi等人提出适应学习率算法
跟踪每个参数的平方和, 必须加平方根
接收到高梯度值的权重更新的效果被减弱,而接收到低梯度值的权重的更新效果将会增强
eps防止出现0的情况
缺点:学习率太激进,容易过早停止学习。
RMSprop 高效,且没被发表的适应性学习率法,Hinton coursera
就是去除了Adagrad的缺点,慢慢降低了学习率。
cache = decay_rate * cache + (1 - decay_rate) * dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)
超参数decay_rate,多用[0.9,0.99,0.999]
# Assume the gradient dx and parameter vector x
cache += dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)
Adam RMSProp的动量版
m = beta1*m + (1-beta1)*dx
v = beta2*v + (1-beta2)*(dx**2)
x += - learning_rate * m / (np.sqrt(v) + eps)
论文中推荐的参数值eps=1e-8, beta1=0.9, beta2=0.999
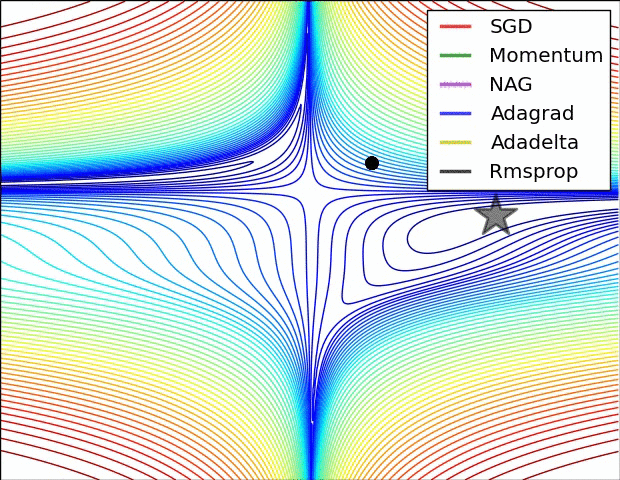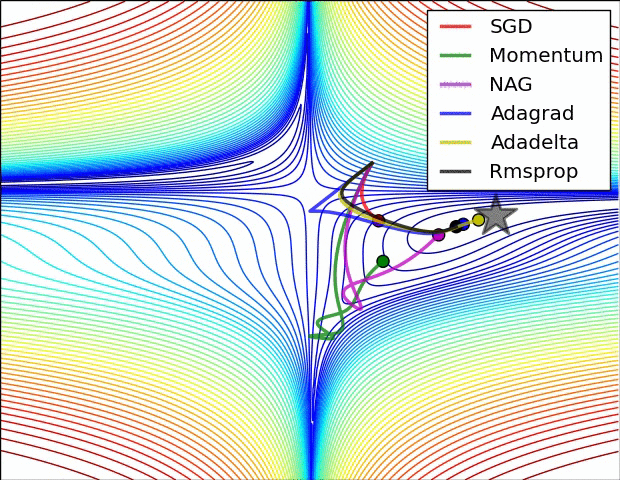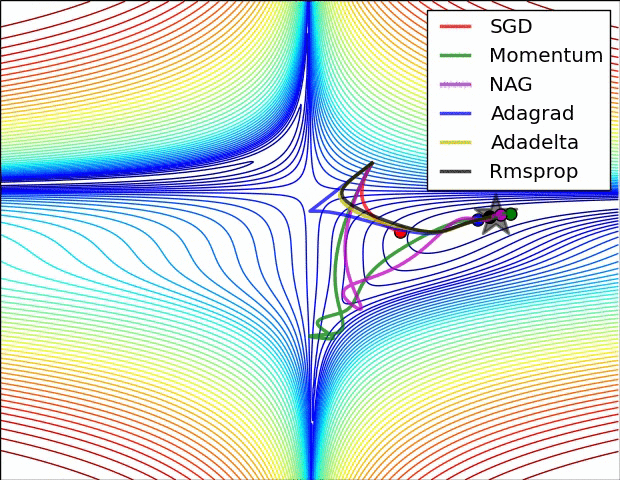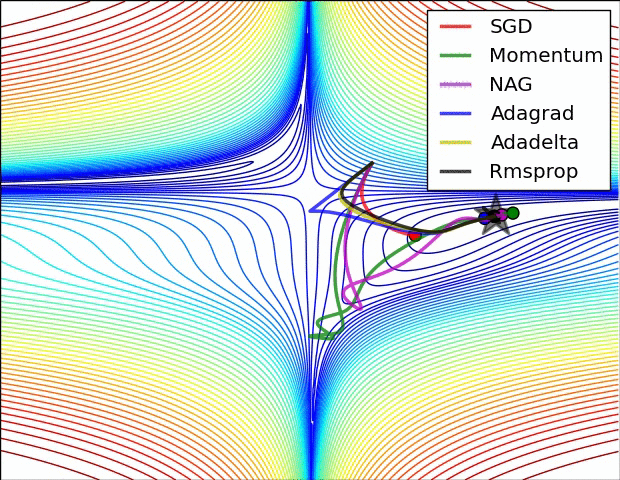
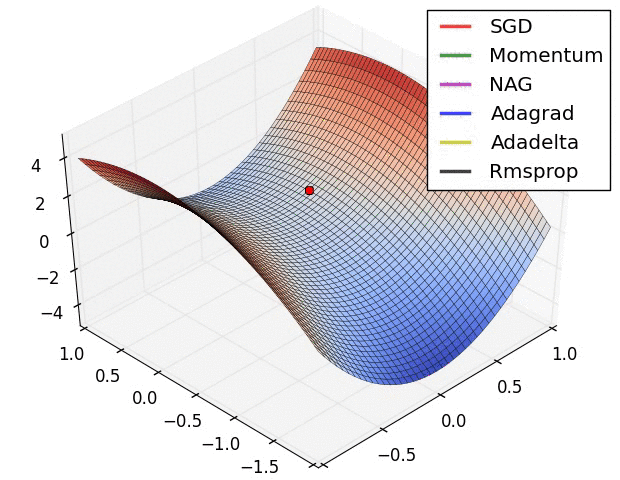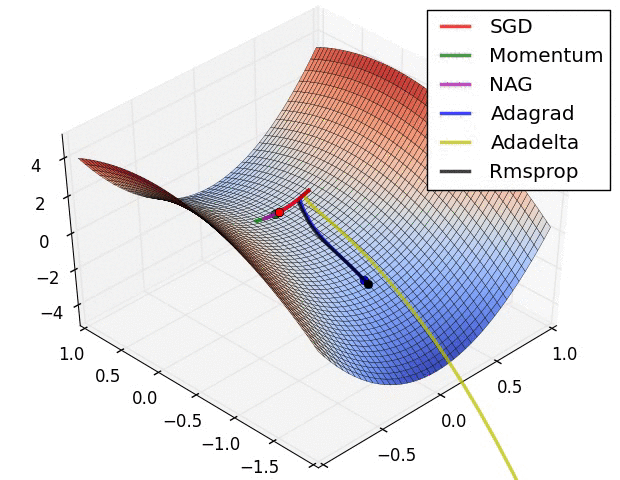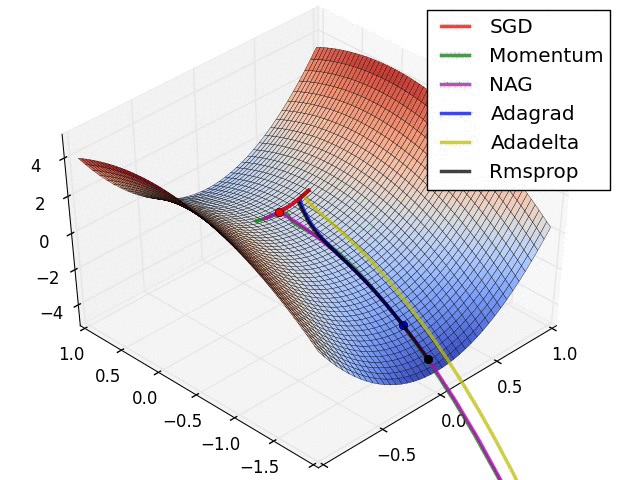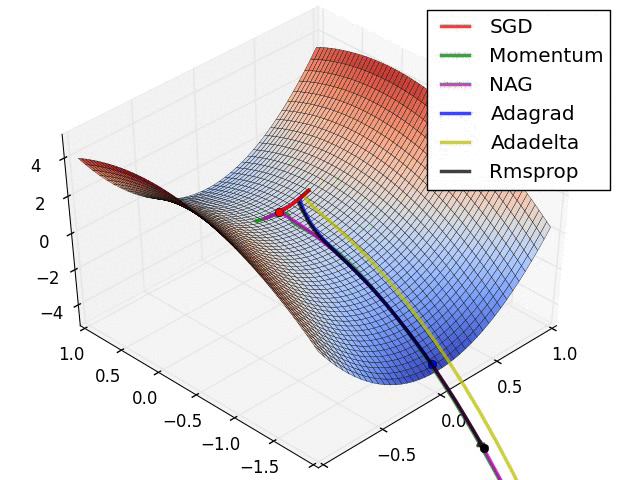
RMSProp更新, 方法中的分母项, 所以动量类的可以继续前进
图片版权:Alec Radford。
6. 超参数优化
总结一下:
- 初始化学习率
- 学习率衰减
- 正则化强度
交叉验证最好使用一个验证集
超参数的范围:learning_rate = 10 ** uniform(-6, 1) dropout=uniform(0,1)
随机选择好于网络搜索
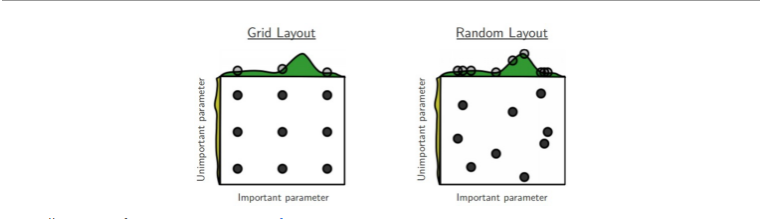
大范围搜索——————>>>贝叶斯超参数优化
7. 评估(集成模型)
提升准确率的办法: 训练独立几个模型,然后平均结果
模型设置多个记录位点: 记录网络值。
跑参数平均值:也可以提上几个百分点,对网络的权重进行备份。
8. 总结
训练网络:
- 小批量梯度检查
- 小批量期间得到100%准确率
- 跟踪损失准确率以及第一层权重可视化
- 权重更新方法:SGD+Nesterov动量法,Adam法
- 学习率衰减
- 随机搜索超参数
- 集成模型(比赛得奖的几乎都用了集成)
9. 附录拓展
Leon Bottou:《SGD要点和技巧》。
Yann LeCun:《Efficient BackProp》。
Yoshua Bengio:《Practical Recommendations for Gradient-Based Training of Deep Architectures》
( y − X w ) T ( y − X w ) (y-Xw)^T(y-Xw) (y−Xw)T(y−Xw)
= ( y T − w T X T ) ( y − X w ) = (y^T-w^TX^T)(y-Xw) =(yT−wTXT)(y−Xw)
= y T y + y T − ( w T X T ) y + w T X T ( X w ) = y^Ty + y^T - (w^TX^T)y + w^TX^T(Xw) =yTy+yT−(wTXT)y+wTXT(Xw)
= y T y − y T ( X w ) − ( X w ) T y + w T ( X T X ) w = y^Ty - y^T(Xw) - (Xw)^Ty + w^T(X^TX)w =yTy−yT(Xw)−(Xw)Ty+wT(XTX)w
= y T y − 2 w T ( X T y ) + w T ( X T X ) w = y^Ty - 2w^T(X^Ty) + w^T(X^TX)w =yTy−2wT(XTy)+wT(XTX)w
A T B = B T A ? A^TB = B^TA ? ATB=BTA?
转载和疑问声明
如果你有什么疑问或者想要转载,没有允许是不能转载的哈
赞赏一下能不能转?哈哈,联系我啊,我告诉你呢 ~~
欢迎联系我哈,我会给大家慢慢解答啦~~~怎么联系我? 笨啊~ ~~ 你留言也行
你关注微信公众号1.机器学习算法工程师:2.或者扫那个二维码,后台发送 “我要找朕”,联系我也行啦!

(爱心.gif) 么么哒 ~么么哒 ~么么哒
码字不易啊啊啊,如果你觉得本文有帮助,三毛也是爱!
我祝各位帅哥,和美女,你们永远十八岁,嗨嘿嘿~~~


这篇关于# [cs231n (七)神经网络 part 3 : 学习和评估 ][1]的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







