数据结构知识铺垫2：物理结构与逻辑结构

本文主要是介绍数据结构知识铺垫2：物理结构与逻辑结构，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

本篇文章的目的在于介绍物理结构与逻辑结构，并对数据结构这门课程做一个比较浅显的概括（不包括排序和查找），使得读者能够对这门课程有一个整体的认识。

1. 物理结构

物理结构研究的是数据在内存中的组织结构。上次我们简单认识了内存（数据结构知识铺垫），现在就让我们思考一下，数据是如何组织在内存中的？对于单个数据，很简单，一个数据对应一个内存单元即可。但是在实际问题中，我们通常要处理一堆数据，如何将一堆数据存储在内存中？也很简单，无非两种情况：连续存储和非连续存储。以{1,3,5,7,9}这五个数字为例，我们探讨一下它们在两种存储方式下的组织形式。

1. 连续存储

顾名思义，连续存储就是在内存中为这五个数字分配一片连续的存储空间。如下图：

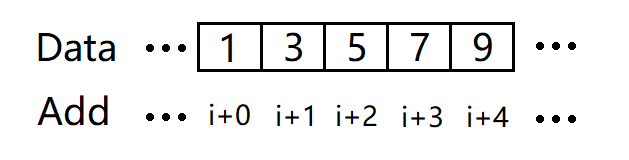
图1. 连续存储

如图（Add为Address的缩写），我们在内存中找到了五个连续的存储空间，用以存储这五个数字，其起始地址为i，对于这五个数字我们只需知道第一个数字的地址i，则其余四个数字的地址我们就都知道了，比如数字5的地址就是i+2。这种可以瞬间推算出某个元素的存取方式，称为随机存取（说成任意存取更好理解一点，即只要知道了首个元素的地址，我们就可以任意地访问连续存储的所有元素）。数组就是一种常见的连续存储方式。

2. 非连续存储

有时候，我们要处理的数据过多，那么为这么多数据分配一片连续的存储空间就很困难，因为内存可能没有那么大的连续存储空间供我们使用，这时，我们就需要用到非连续存储。仍以{1,3,5,7,9}为例，看一下如何用非连续存储方式存储它们。

图2. 非连续存储（1）

如图，我们在内存中找到了五个不连续的存储空间，其地址分别为a，b，c，d，e。用来存储这五个数字，看上去很完美，但是要注意，既然存储空间不是连续的，即使我们知道了第一个数字的地址，我们也无法通过随机存取来获取其余四个数字的地址，因为a，b，c，d，e这五个地址没有任何关系。怎么解决这个问题？至少我们需要知道这五个数字的全部地址。这里假设五个数字之间的关系是线性的（即线性表，以后详述），则{1,3,5,7,9}就有了前驱与后继的关系。比如3的前驱是1，后继是5。只要我们知道了这种关系，同样可以在知道第一个数字的地址后，取得其余四个数字。假如我们这里只考虑后继关系，现在要把这种后继关系组织在内存中，可以这样做：在每个数字的存储的地方，再多存储一个东西，即该数字的后继数字的地址。如下图：

图3. 非连续存储（2）

通过存储后继关系，通过存储后继关系，我们就只需要知道第一个数字的地址，即可取得其余所有数字。比如取5这个数字，我们可以先通过第一个数字的地址a，找到第一个数字1，然后又知道1的后继的地址是b，就可以通过地址b，取得第二个数字3，再通过3的后继的地址是c，就可以再通过地址c，取得数字5。这里要注意的一个问题是：为什么我们可以在数字存储的地方再存储一个后继的地址呢？一个内存单元不是只能存储一个数据吗？回想一下上篇文章“数据结构知识铺垫”中，我们提到过抽象的思想，即我们把多个内存单元看做一个整体，但地址仍抽象为原来的地址，这里也是同样的道理，这里的a，b，c，d，e也是经过抽象后的地址，方便我们研究问题使用。现在，让我们用箭头来指代每个存储结点的地址，让其指向每个结点的后继结点，如下图：

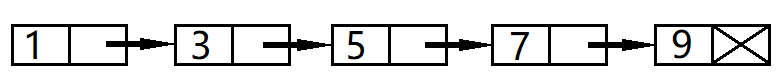
图4. 非连续存储（3）

可以看出，我们通过非连续存储方式将五个数据组织了起来，它们的形式看起来像是一个链条，因此非连续存储方式又称为链式存储。这种以链式存储的线性表称为链表。通常链表的第一个结点我们不存储任何数据，称为头结点，当然这是后话了，以后细讲。

2. 逻辑结构

物理结构的研究重点是数据在内存（硬件）上的存储方式，而逻辑结构的研究重点在于数据之间的逻辑关系。这么说可能有些抽象，我们可以从简单的问题入手：用一些圆圈来代替数据，现在我们要把这些圆圈（数据）连接起来，它们之间有哪些连接方式呢？

①什么连接都没有，也即这些数据是孤立的，如下图：

图5. 集合

这种结点之间没有任何联系的结构称为集合，不过这种逻辑结构在数据结构中没有太大的意义，因此不是研究的重点。

②用一条“线”把所有的结点“串”起来，但首尾并不相连，如下图：这种结构称为线性结构。

图6. 线性结构

③在线性结构中，每个结点（头尾结点除外）都只能有一个前驱和一个后继，如果我们只限制前驱的个数最多为1，而不限制后继的个数，就得到了树形结构，如下图：

图7. 树形结构

④如果我们继续放宽限制，不再约束前驱的个数，即结点的前驱个数可以有多个，则可以得到图状结构，如下图：

图8. 图状结构

到这里，我们罗列了结点之间所有的可能的简单逻辑关系，你可能会问：了解这些有什么用？撇开集合不谈，我们思考一下另外三种逻辑结构的应用场景：

线性表：这个逻辑结构的应用场所就很多了，比如一个班级中每个学生的成绩排名，在没有相同分数的情况下，每个学生的排名是固定的，即每个分数数据都最多只有一个前驱和一个后继。

树形结构：比如电脑文件夹的层级结构，又比如家族之间的血缘关系。

图状结构：比如QQ的好友，若A与B互为好友，则他们之间就可以用“线”连起来，这样一个社交圈子之间的人的关系就可以用图来表示了。

3. 用物理结构存储逻辑结构

在了解了物理结构与逻辑结构之后，你可能还是不太清楚两者之间的关系，不要急，我们先来思考一下，我们在解决问题时，分析出了所需要的逻辑结构，但逻辑结构是给我们人看的，不是给计算机看的。比如图状结构，我们可以轻松地画出一群人之间的好友关系图，但计算机并没有那么聪明，它并不能直接得出这个图，因为计算机只有一块死板的内存可以用。这时我们不禁要思考：如何把我们可以看懂的逻辑结构，让计算机可以看懂呢？换句话说，如何把我们可以看懂的逻辑结构存储到计算机的内存里面呢？想到这里，我们就有点头绪了，因为我们已经学习了计算机的内存的结构，即物理结构。所以现在的问题就是：如何用物理结构来存储逻辑结构？不急，我们按照线性表、树形结构、图状结构的顺序一个个来分析。

1. 线性表

我们知道对于物理结构有两种存储方式：连续存储和非连续存储（链式存储）。那么在我们分析线性表时也要分这两种情况来讨论。而在本篇文章开头，我们探讨连续存储和非连续存储时，举的例子所用的逻辑结构就是线性表，因此这里不再赘述。

2. 树形结构

这里我们以满二叉树为例进行讲解，所谓满二叉树，就是除最后一层无任何子结点（子结点就是前面说的后继结点）外，每一层上的所有结点都有两个子结点的二叉树（具体定义可以百度）。同样地，分连续存储和非连续存储两种情况讨论。

1.连续存储下的树形结构

首先观察一下一颗满二叉树，如下图：

图9. 满二叉树

我们要意识到，满二叉树是约束条件很多的一棵树，限制越多，就越容易发现结点之间的规律与联系。现在我们就为每个结点从上到下、从左到右依次编号（从0开始编号），来观察一下结点编号之间的规律，如下图：

图10. 给满二叉树编号

可以看出，设某个结点的编号为k，则该结点的左孩子结点的编号必为2 * k + 1，右孩子结点的编号必为2 * k + 2。怎么把这个规律运用到连续存储方式中呢？对于连续存储方式，我们常用的一种存储方式是数组，不过数组直觉上好像只能存储线性表，但事实上并非如此。在我们面前的这棵满二叉树，它们的结点编号之间有着很明显的线性关系，能否把这棵满二叉树存储到数组中呢？显然是可以的。因为我们都把编号写出来了，只需要按照这些编号，在对应的数组下标中存储对应的结点即可。如下图：

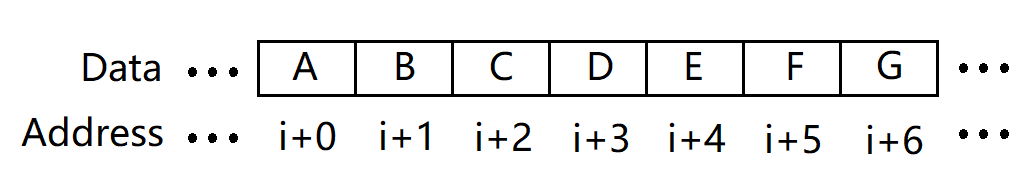
图11. 连续存储下的树形结构

看到你肯定会有疑问：不对呀，这不是连续存储下的线性表吗？怎么是一棵树呢？注意，在物理结构中，我们只讨论连续存储与非连续存储（其实还有散列表，这是后话），并不考虑逻辑结构层面中的内容。就好比作为一台计算机，它只知道数据在内存中是连续存储还是非连续存储的，并不知道存储的内容是线性表、树或者图，因为逻辑结构是我们人类需要考虑的内容。所以说，对于内存中连续存储的一片数据，以不同的方式进行解读，会得到不同的逻辑结构。现在就让我们忘掉图9和图10，以满二叉树的方式，对图11进行解读。已知图11存储了一棵满二叉树，如何从这一片连续存储的数据得到一棵满二叉树？我们前面已经得到了结点编号之间的规律了，因此只要知道某个结点的编号（数组下标），就可以得到它的左右孩子的编号（数组下标）。而对于一个数组，我们只知道首个数据的地址，但这已经足够。已知A的地址为i，下标为0，则A的左、右孩子结点的地址必为i + 0 * 2 + 1和i + 0 * 2 + 2，即A的左右孩子结点的地址为i + 1和i + 2，故A的左右孩子分别为B和C。同理可得其他结点之间的逻辑关系，就这样，我们根据一片连续存储的数据得到了一棵满二叉树。

2. 非连续存储下的树形结构

这里仍以满二叉树为例。回顾一下图4，在非连续存储方式下，我们可以把某个结点的后继结点的地址抽象为一个箭头，使其指向后继结点，从而得到了线性表的逻辑结构。这里也是同样的思想，不过是反过来，我们可以把图9中的直线改成箭头，如下图：

图12. 满二叉树（2）

这样你肯就有些思路了：在每个结点的后面再存储一下后继结点的地址，就可以把树以非连续方式存储起来了。假设我们已经在内存中找到了几个不连续的内存空间，并将各个结点存储了起来，如下图：

图13. 非连续存储下的树形结构（1）

如图，结点A对应的内存地址为a，以此类推。我们只需要在每个结点后面再存储一下后继结点的地址，即可将树形结构以非连续方式存储，如下图：

图14. 非连续存储方式下的树形结构（2）

如图，在每个结点的第二个存储单元存储左孩子的地址，第三个存储单元存储右孩子的地址。这样就把树形结构的逻辑关系用非连续存储方式存储了下来。至于如何通过该图得到一棵树，也很简单，以结点A为例，b是A的左孩子的地址，就去找地址b对应的数据，即B，故B为A的左孩子；c是A的右孩子的地址，就去找地址c对应的数据，即C，故C为A的右孩子。其余结点同理。因此，我们同样可以用非连续存储方式来存储一棵树。

3. 图状结构

首先，我们准备一个简单的图，如下：

图15. 一个简单的图

1. 连续存储下的图状结构

通过对线性表、树的存储，我们应该认识到，在物理结构层面（内存中），只存储数据是不够的，我们还要在物理结构层面上存储对应的数据之间的逻辑关系，才能得出数据之间的逻辑结构。这里对图的存储也是一样的，我们也要想办法存储图的数据之间的逻辑关系。图的结点（数据）之间的逻辑关系是什么样子的？看上去似乎很难回答，因为每个结点跟其余的所有结点都有可能有联系，我们不妨极端地思考一下：假设有n个结点，每个结点跟其余的所有结点都有联系，则每个结点都会引出n - 1条线，因此结点之间的连线不会超过n²条，这样的话，一个n*n的矩阵就可以包含n个结点所有可能的联系。具体做法如下：如果两个结点之间有联系，就记为1；如果两个结点没有联系，就记为0。以图15为例，先将各个结点的阵列表示出来，如下图：

图16. 图的结点阵列

如图，每两个结点可以确定图中的一个空格子，而每两个结点之间又只有两种可能：有连接或者没有连接。因此我们可以在空格子里面填上0或1，0代表没有连接，1代表有连接，如下图：

图17. 用矩阵存储结点的连接关系

看到这些4 * 4排列的数字，有没有感觉很熟悉？没错，我们得到了一个矩阵，这个矩阵可以很好地存储图的结点之间的连接关系，称为邻接矩阵。如果你观察地更仔细一点，会发现这个矩阵是对称的。这并不是巧合，以矩阵的左下角的元素（记为M41）和右上角的元素（记为M14）为例，它们都是1，即代表存在连接。M41代表D与A之间有连接，M14代表A与D之间有连接。因为我们这里给出来的图的结点之间的连接是没有方向的（称为无向图），因此D与A的连接和A与D的连接是一样的。可以看出，A与D之间的一条连接，我们存储了两次。其余所有的连接都是如此。所以得到的一定是一个对称矩阵。

现在，我们有了图的逻辑结构的矩阵表示，下面就可以思考如何存储这个逻辑结构了。这是显而易见的：将矩阵存储起来即可。而在连续存储方式下，存储一个矩阵的方式就更简单了：用一个二维数组即可。但这里我们要再进一步思考一下：我们得到的矩阵是对称矩阵，因此我们只需要知道主对角线上的元素以及主对角线上方的元素，就可以通过对称性得到整个矩阵了。因此用一个二维数组来存储一个矩阵显然是比较浪费的，因为那样将存储大量的重复元素，造成内存空间的浪费。所以我们只需要用一个一维数组来存储即可。你可能会问：一维数组怎么够用？别急，我们先来观察一下我们要存储的数据，如下图：

图18. 要存储的数据

如图，可以看出很明显的规律：对于一个n * n的对称矩阵，我们要存储的元素个数为N = 1 + 2 + 3 + …… + n = （1 + n）* n / 2。因此可以定义一个长度为N =（1 + n）* n / 2的数组。现在我们规定先存储第一行的n个元素，再存储第二行的n - 1个元素……以此类推。而在每行中，从左到右依次存储元素。（这种存储方式称为行优先存储）。这样就可以把所有的数据存储在一个一维数组中了。以图18为例，则在一维数组中依次存储的数据为：0,1,1,1,0,1,0,0,0,0。这样我们就把图的逻辑结构用连续存储方式存储了下来。

你可能还是不太习惯这种存储方式：这个一维数组怎么就存储了一张图了呢？那我们就反过来思考一下，已知一个一维数组中的元素为{0,1,1,1,0,1,0,0,0,0}，并且这个一维数组按照行优先存储方式存储了一个4 * 4的对称矩阵的上半部分，如何得到这张图？很明显在这样的存储方式下，数组的前四个元素是矩阵的第一行，紧跟着的三个元素是矩阵的第二行元素，以此类推，就可以得到图18中的矩阵。进而就可以得到图17中的整个矩阵，再用A，B，C，D分别表示四个结点，就可以画出每两个结点之间的连接关系。比如M13为1，则说明A与C之间有连接关系。进而就可以得到整张图。