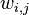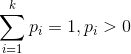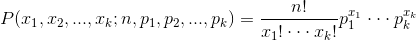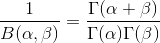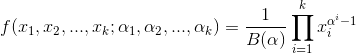LDA主题模型--原理讲解1：铺垫和基础

1、铺垫

        最开始听说“LDA”这个名词，是缘于rickjin在2013年3月写的一个LDA科普系列，叫LDA数学八卦，不知是因为这篇文档的前序铺垫太长，还是因为其中的数学推导细节太多，导致一直没有完整看完过。现在才意识到这些“铺垫”都是深刻理解LDA 的基础，如果没有人帮助初学者提纲挈领、把握主次、理清思路，则很容易陷入LDA的细枝末节之中，LDA模型的数学推导是比较复杂的

        LDA有两种含义，一种是线性判别分析（Linear Discriminant Analysis），一种是概率主题模型：隐含狄利克雷分布（Latent Dirichlet Allocation，简称LDA）

        LDA可以分为下述5个步骤：           

•             一个函数：gamma函数
•             四个分布：二项分布、多项分布、beta分布、Dirichlet分布
•             一个概念和一个理念：共轭先验和贝叶斯框架
•     两个模型：pLSA、LDA
•             一个采样：Gibbs采样

2、解释LDA的小案例

        LDA由Blei, David M.、Ng, Andrew Y.、Jordan于2003年提出，是一种主题模型，它可以将文档集 中每篇文档的主题以概率分布的形式给出，从而通过分析一些文档抽取出它们的主题（分布）出来后，便可以根据主题（分布）进行主题聚类或文本分类。同时，它是一种典型的词袋模型，即一篇文档是由一组词构成，词与词之间没有先后顺序的关系。
        此外，一篇文档可以包含多个主题，文档中每一个词都由其中的一个主题生成。

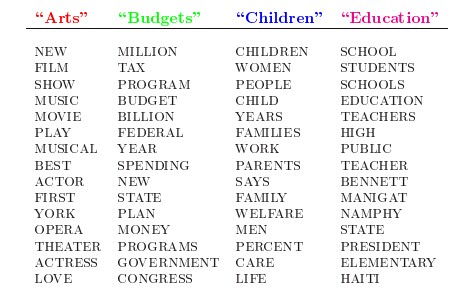
        怎么生成文档？LDA的这三位作者在原始论文中给了一个简单的例子。比如假设事先给定了这几个主题：Arts、Budgets、Children、Education，然后通过学习训练，获取每个主题Topic对应的词语。如下图所示：

        然后以一定的概率选取上述某个主题，再以一定的概率选取那个主题下的某个单词，不断的重复这两步，最终生成如下图所示的一篇文章（其中不同颜色的词语分别对应上图中不同主题下的词）：

        而当我们看到一篇文章后，往往喜欢推测这篇文章是如何生成的，我们可能会认为作者先确定这篇文章的几个主题，然后围绕这几个主题遣词造句，表达成文。

        LDA就是要干这事：根据给定的一篇文档，反推其主题分布。

        通俗来说，可以假定认为人类是根据上述文档生成过程写成了各种各样的文章，现在某小撮人想让计算机利用LDA干一件事：你计算机给我推测分析网络上各篇文章分别都写了些啥主题，且各篇文章中各个主题出现的概率大小（主题分布）是啥。

        然，就是这么一个看似普通的LDA，一度吓退了不少想深入探究其内部原理的初学者。难在哪呢，难就难在LDA内部涉及到的数学知识点太多了。

        在LDA模型中，一篇文档生成的方式如下：

• 从狄利克雷分布中取样生成文档 i 的主题分布
• 从主题的多项式分布中取样生成文档i第 j 个词的主题
• 从狄利克雷分布中取样生成主题对应的词语分布
• 从词语的多项式分布中采样最终生成词语

其中，类似Beta分布是二项式分布的共轭先验概率分布，而狄利克雷分布（Dirichlet分布）是多项式分布的共轭先验概率分布。

此外，LDA的图模型结构如下图所示（类似贝叶斯网络结构）：

        短短6句话整体概括了整个LDA的主体思想，却接连不断或重复出现了二项分布、多项式分布、beta分布、狄利克雷分布（Dirichlet分布）、共轭先验概率分布、取样 ，具体如何往下看

3、各种分布和附带数学知识讲解

•  二项分布（Binomial distribution）

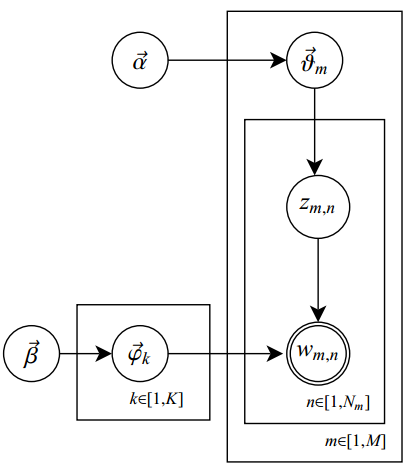
        二项分布是从伯努利分布推进的。伯努利分布，又称两点分布或0-1分布，是一个离散型的随机分布，其中的随机变量只有两类取值，非正即负{+，-}。而二项分布即重复n次的伯努利试验，记为 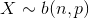。简言之，只做一次实验，是伯努利分布，重复做了n次，是二项分布。二项分布的概率密度函数为：

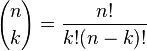
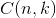
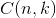
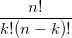
        对于k = 0, 1, 2, ..., n，其中的是二项式系数（这就是二项分布的名称的由来），又记为。回想起高中所学的那丁点概率知识了么：想必你当年一定死记过这个二项式系数就是。 

• 多项分布，是二项分布扩展到多维的情况。

       多项分布是指单次试验中的随机变量的取值不再是0-1的，而是有多种离散值可能（1,2,3...,k）。比如投掷6个面的骰子实验，N次实验结果服从K=6的多项分布。其中

多项分布的概率密度函数为：

•  Beta分布，二项分布的共轭先验分布

        给定参数和，取值范围为[0,1]的随机变量 x 的概率密度函数：

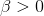
        其中：

          注：便是所谓的gamma函数，下文会具体阐述。

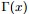
• Dirichlet分布，是beta分布在高维度上的推广

​​​​​​​        Dirichlet分布的的密度函数形式跟beta分布的密度函数如出一辙：

         其中

         总结就是：

            二项分布和多项分布很相似，Beta分布和Dirichlet 分布很相似

            beta分布是二项式分布的共轭先验概率分布，而狄利克雷分布（Dirichlet分布）是多项式分布的共轭先验概率分布