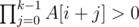本文主要是介绍暑假训练day1 : 2016 USP-ICMC，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
发挥还算不错。。。
传送门：http://codeforces.com/gym/101063
https://vjudge.net/contest/169377#overview
It is the year of 2016 and Mars is still not colonized. A daring group of immortal, rich explorers based in São Carlos decided that it is about time to do something about it, so they founded a space exploration company called GEMA - Go Explore Mars Already!
Fast forward to 2017. The first mission of GEMA has finally landed on Mars, but it seems like the rocket fell in the middle of some ancient ruins that form a giant maze resembling a snail. The maze is composed of Ncircular sectors all centered at the crash site of the rocket.
The circular sectors of the maze all have a railway running through their middle, and some portions of the walls are open, making it possible to leave to the next sector. The rails connecting sectors are straight, radial lines through the opening, connecting the rails of the two sectors. There is always a straight line connecting the crash site to the first sector railway through the openings. The only safe way to travel in this maze is by using these rails.
The crew of the GEMA mission wants to leave the maze as soon as possible. Luckily, they are in possession of small carts that fit the railway. Help them find the path with the minimum length to leave the maze. You are out of the maze as soon as you cross the boundary of the outermost wall.
The above figure illustrates the first sample test case. Dashed lines represent the railways that run through the middle of the sectors, whose boundaries are represented by solid circles. The best solution in this case is to go from points A, B, C, D and then E, going through the sectors railways through points X, Y, W and Z, as indicated by the green line.
The input begins with an integer N (1 ≤ N ≤ 105), the number of circular sectors of the Snail Maze. The next line has N integers r, the radius of each of the sectors (1 ≤ r ≤ 109). The next line contains an integer Q (N ≤ Q ≤ 105), the number of openings. The next Q lines contains an integer and a real number each. The first integer, ri (1 ≤ ri ≤ 109) gives the radius of a wall (that radius will be one of the N numbers given in the second line), and the real number d, gives the angle, in radians, where the opening is located (0 ≤ d ≤ 2π). The angle is measured in clockwise direction with respect to west (the positive x-axis).
It is guaranteed that there is a path to leave the maze, i.e., every wall has at least one opening. There will not be two openings closer than 10 - 4 radians.
Output the length of the shortest path to leave the maze. Your answer will be considered correct if its absolute or relative error does not exceed 10 - 6.
3 4 10 6 4 4 1.0472 4 1.5707 6 4.7123 10 4.1857
27.30323
构图比较难搞，待补
比赛时候超时还以为是复杂度太高，用位运算搞了个O(n)算法，其实是死循环，没有考虑m=1。还好最后一分钟绝杀此题。
#include <cstdio>
#include <iostream>
#include <string.h>
#include <queue>
#include <vector>
#include <math.h>
#include <map>
#include <stdlib.h>
#include <algorithm>
using namespace std;
typedef long double ld;
int a[256][25],b[20][25],pitch[10005];
char s[23];int main() {int n,m,i,j,k;char c;scanf("%d",&m);map<char,int> my;my['A']=1;my['B']=2;my['C']=3;my['D']=4;my['E']=5;my['F']=6;my['G']=7;my['#']=7;my['b']=14;memset(a,0,sizeof(a));memset(b,0,sizeof(b));for (i=1;i<=m;i++) {for (j=1;j<=7;j++) {scanf("%s",s);if (strlen(s)==1) {b[i][my[s[0]]]=1;} else {b[i][my[s[0]]+my[s[1]]]=1;}}}int l=0;if (m!=1)for (i=1;i<=m;i++) {for (j=i+1;j<=m;j++) {l++;for (k=1;k<=21;k++) {a[l][k]=b[i][k]+b[j][k];if (a[l][k]) a[l][0]=a[l][0]|(1<<(k-1));}}}else {l=1;for (k=1;k<=21;k++) {a[l][k]=b[1][k];if (a[l][k]) a[l][0]=a[l][0]|(1<<(k-1));}}scanf("%d",&n);for (i=1;i<=n;i++) {scanf("%s",s);if (strlen(s)==1) {pitch[i]=my[s[0]];} else {pitch[i]=my[s[0]]+my[s[1]];}}int maxlen=1,maxcondition,cnt=0;while (maxlen<=n) {cnt++;maxcondition=0;for (j=1;j<=l;j++) {if (maxcondition!=(maxcondition&a[j][0])) continue;while (a[j][pitch[maxlen]]&&maxlen<=n) {maxcondition=(maxcondition|(1<<(pitch[maxlen]-1)));maxlen++;}}}printf("%d\n",cnt);return 0;
}It is nighttime in the Earth Colony on Mars and everyone is getting ready to sleep. It is common to sleep in pairs, so that if anything were to happen during the night people could aid each other.
To decide who is a suitable candidate to sleep with whom, the leaders of GEMA asked everyone to answer a questionnaire about attributes they desire their partner to have from a list of M possible items.
To choose the pairs, GEMA uses the Jaccard index between the desired attributes of both persons. The Jaccard index for two sets A and B is defined as 
, that is, the size of the intersection between A and B divided by the size of their union. They allow a pair to be formed if the Jaccard index of the two attribute sets for the pair is at least K.
Thanks to GEMA, there are too many people living on Mars these days. Help the high commanders decide how many allowed pairs there are out of the N people living there.
The input begins with two integers, N and M (1 ≤ N ≤ 105, 1 ≤ M ≤ 10), the number of people on Mars and the number of possible attributes on the questionnaire.
Then follow N lines, each beginning with an integer Q (1 ≤ Q ≤ M), the number of desired attributes on the list of the i-th person. Then follow Q integers q (1 ≤ q ≤ M), encoding these attributes. There numbers are all different.
The last line of input contains a real number K (0 ≤ K ≤ 1), the minimum required Jaccard index for a pair.
Output the number of pairs that are allowed.
2 5 2 1 3 5 3 1 5 4 2 0.66489
0
3 1 1 1 1 1 1 1 0.85809
3
#include <cstdio>
#include <iostream>
#include <string.h>
#include <queue>
#include <vector>
#include <stack>
using namespace std;
typedef long double ld;
typedef long long ll;
const int maxn=100005;
int a[maxn][11],b[maxn];
ll c[(1<<10)+5],d[maxn];int main() {int n,m,q,i,j;ld k;scanf("%d%d",&n,&m);memset(c,0,sizeof(c));for (i=1;i<=n;i++) {scanf("%d",&a[i][0]);b[i]=0;for (j=1;j<=a[i][0];j++) {scanf("%d",&a[i][j]);b[i]+=(1<<(a[i][j]-1));}c[b[i]]++;}cin >> k;ll ans=0;for (i=1;i<=1023;i++) {int l=i;d[i]=0;while (l>0) {if (l%2) d[i]++;l/=2;}}for (i=1;i<=1023;i++) {for (j=i;j<=1023;j++) {int q=i&j,w=i|j;ld ratio=(ld)d[q]/(ld)d[w];if (ratio>=k) {if (i!=j) ans+=c[i]*c[j]; else ans+=c[i]*(c[i]-1)/2;}}}printf("%I64d\n",ans);
}
#include <cstdio>
#include <iostream>
#include <string.h>
#include <queue>
#include <vector>
#include <stack>
using namespace std;
int a[105][105];int main() {int n,k; cin >> n >> k;if ((n+1)%k==0) cout << "yes\n"; else cout << "no\n"; return 0;
}A lot of people, still living on Earth, dream of one day getting the opportunity to go to Mars and be a GEMA explorer. It's so glamorous and important, everything is so exciting, so different from the regular boring life on Earth.
However, the reality of the regular folk on Mars is not as nearly glamorous as everyone thinks. A day of an average explorer is at least as boring as a day of any Earth-living human. Every week, GEMA assigns tasks to each explorer in the expedition. Most of the times, these tasks are just very long and detailed reports they have to make. The worst part is that, after completing it, you would still have to review reports from your colleagues and correct them if mistakes are found.
One type of report consists of reporting collected data, but, before making the report, one should verify the consistency of the data. This is obviously the most boring part, so it is not surprising that some people prefer to skip it and just write the report without any verification.
To make matters worse, when reviewing a report containing contradictory data, instead of canceling the report, some explorers choose to manipulate the data, changing some numbers, so it would become consistent. This happens because canceled reports are seen as a great incompetence of the whole team who worked on it.
You are a GEMA explorer and you've just received a report. You need to manipulate the data on it, in order to make it seem correct. The data of the report is a bunch of positive or negative numbers. The data is considered consistent if and only if every sub-array of length k has a positive result when all numbers in it are multiplied together.
Formally, if the report is an array A of N positive and/or negative numbers, the report is consistent, if and only if, for all 1 ≤ i ≤ N - k + 1, we have:
Answer what is the least number of changes you have to make in the report so it would become consistent. A change in the report is changing the value of one of its numbers.
The input begins with two integers N and k (1 ≤ k ≤ N ≤ 5 × 105) in a single line. The next line will contain N integers ai ( - 100 ≤ ai ≤ 100 and ai ≠ 0).
One integer, the answer to the task.
3 1 10 -100 33
1
5 5 1 -1 -2 3 4
0
5 3 1 -1 -2 3 4
1
序号相差k的数字，满足题中式子时正负性一定相等。把极性相同的数字改成同一符号即可。取正还是负呢？枚举前k个数有0,2，...2n个负数的情况，贪心更新最优解。
#include <cstdio>
#include <iostream>
#include <string.h>
#include <queue>
#include <vector>
#include <math.h>
#include <stack>
#include <algorithm>
using namespace std;
const int maxn=500005;
int a[maxn];struct Node {int b,c;
} node[maxn];bool cmp(Node x,Node y) {return x.b-x.c>y.b-y.c;
}int main() {int n,i,k,j,ans=0,sum=0;memset(node,0,sizeof(node));scanf("%d%d",&n,&k);for (i=1;i<=n;i++) {scanf("%d",&a[i]);if (a[i]<0) node[i%k].b++; else node[i%k].c++;}sort(node,node+k,cmp);for (i=0;i<k;i++) {sum+=node[i].b;}ans=sum;for (i=1;i<k;i+=2) {sum+=node[i].c+node[i-1].c;sum-=node[i].b+node[i-1].b;ans=min(ans,sum);}printf("%d",ans);return 0;
}
#include <cstdio>
#include <iostream>
#include <string.h>
#include <queue>
#include <vector>
#include <stack>
#include <iomanip>
using namespace std;
typedef long double ld;
const int maxn=100005;
int a[maxn];int main() {int n,k,i,j,q=0;scanf("%d%d",&n,&k);for (i=1;i<=n;i++) {scanf("%d",&a[i]);if (i>1&&a[i]!=a[i-1]) q++;}ld ans=(ld)(k-1)/(ld)k;ans*=(ld)q;cout << setiosflags(ios::fixed) << setprecision(9);cout << ans;return 0;
}Half a century after the Mars arrival by GEMA, we are finally here. The mission is finally starting to build artificial rivers on mars.
That is possibly the most important event on Mars since the GEMA arrival.
In order to carry on with it, the mission have mapped the surface as 2-dimensional plane, and has identified N points in it that are going to work as reference points to build a river system. There will be a dock constructed in each of these points to help on transportation efforts and collect data for the mission.
The goal of the mission is to connect all the docks with rivers. The lead researcher of the team responsible for that, doctor Maya Waters, has identified the main requirements to build a healthy river system. These are:
- There are N docks. There should be a way to navigate between any two docks only through water;
- The system must have exactly N rivers - no more, no less;
- At most four rivers can meet at any single dock;
- Any river should flow in a straight line between points A and B;
- There should be no river crossings apart from the rivers meeting at docks. Note that a river passing through a dock counts as a crossing.
Help doctor Maya figure out which points to connect to build such river system and finally Make Mars Wet Again!
Input begins with N (3 ≤ N ≤ 103), the number of points. Follows N lines, each with two integers xi, yi( - 109 ≤ xi, yi ≤ 109), the coordinates of the pivotal points.
Output N lines. In each line, output two integers , a and b - the indexes of the pivotal points that must be connected by a river. Indexing begins in 1. If there are multiple solutions, output any.
If it is an impossible task, output -1.
5 -1 0 2 3 3 2 5 4 6 1
3 2 3 4 5 3 1 5 2 4
3 0 0 1 2 3 6
-1
先按坐标排个序，按顺序连起来，再找一条线就可以。剩下的一条线，一端为第一个点，依次枚举。
这篇关于暑假训练day1 : 2016 USP-ICMC的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
