本文主要是介绍论文解读--Compensation of Motion-Induced Phase Errors in TDM MIMO Radars,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
TDM MIMO雷达运动相位误差补偿
摘要
为了实现高分辨率的到达方向估计,需要大孔径。这可以通过提供宽虚拟孔径的多输入多输出雷达来实现。但是,它们的工作必须满足正交发射信号的要求。虽然发射单元的时分复用是一种低硬件成本的正交实现,但在非平稳情况下会出现相位误差。这篇文章简要地讨论了运动引起的相位误差的问题,并描述了处理步骤,没有额外操作就可以减少(误差)。仿真和实测数据验证了该方法的有效性。
1 介绍
目前汽车雷达的发展方向是多输入多输出(MIMO)系统,由M个发射器和N个接收器组成。它们提供了大量的虚拟天线元件和高角度分辨率,与传统系统相比,这减少了硬件和孔径尺寸的工作量。但实现时需要传输正交信号。在线性调频chirp序列雷达中,这通常是通过时间、频率或码分复用来完成的。这篇文章的重点是时分复用(TDM)方案,这是非常常用的[1]-[4]。
chirp序列雷达发射一系列线性频率斜坡。每个的基带时间样本存储在一个矩阵中,用二维傅里叶变换提取距离和速度。这导致了每个单通道的距离-多普勒频谱。当采用TDM MIMO方案时,每次发送单个chirp后,都会改变主动发射单元。图1所示为两个发射机(M=2)的示例。每个发射机和每个接收机的几何位置形成一个虚拟阵列,该阵列的虚拟元素最多有M*N个。为虚拟阵列的每个阵元找到了距离-多普勒频谱。
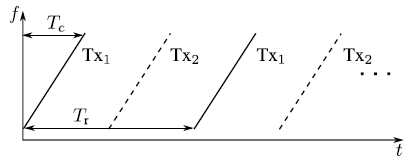
图1 在示例性TDM MIMO方案中,发射机Tx1和Tx2以交替方式工作。Tr限制了不模糊多普勒频率[5]。
天线单元之间的相位差用于到达方向(DoA)估计。在非MIMO线性阵列中,一个信号在两个接收信道上的相位差为
![]() (1)
(1)
其中,θ为信号的入射角,k为波数,d为阵元之间的距离。在如图1所示的TDM MIMO系统中,由于发射机Tx1和Tx2之间的切换时间Tr/2,必须考虑额外的相位差。这使(1)变成
![]() (2)
(2)
目标运动产生多普勒频率fD,引入了额外的相位项。对于具有高fD的目标,![]() 受到此误差的强烈影响。一般来说,对于M个发射机,在第M个发射机处的相位关系Txm为
受到此误差的强烈影响。一般来说,对于M个发射机,在第M个发射机处的相位关系Txm为
![]() (3)
(3)
为了补偿运动引起的相位误差,[6]提出在虚拟孔径中创建重叠阵元。这些阵元用于估计和修正误差;然而,这是以(M−1)个独立虚拟阵元为代价的,因此减小了最大孔径尺寸或最大通道数量。优化发射机的切换方案以减小相位误差在[7]中进行了讨论。文献[8]介绍了运动误差的估计和插值。另一种方法是通过频率坡道的交错传输来减小误差[9]。
在这篇文章中,介绍了一种直接的方法,并演示了用基本的信号处理技术处理chirp序列雷达的运动引起的相位误差。这种方法不需要任何额外的硬件工作,并且只有很小的处理需求。
2 相位误差补偿
在本节中,描述了运动引起的相位误差的来源,并调整了用于提取速度的离散傅立叶变换(DFT)以减轻相位误差。
单频chirp l = 0,1,2,…的基带时间信号的模型与[5]类似为
![]() (4)
(4)
其中c0为光速,fc为chirp的中心频率,R为目标距离。距离相关频率为fR = 2BR/(c0Tc)。对于持续时间短的Tc和高带宽B的chirp,通常假设fR >> fD。傅里叶变换F(sTxm (t, l))得到chrip l的距离谱
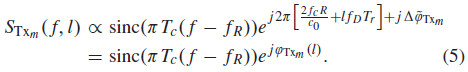
图2显示了在单个发射机Tx1的情况下,单个目标在多个频率chirp下的复矢量STx1 (fR, l)。在这种非MIMO设置中,计算所有chirp的第二次傅立叶变换以提取速度。对于频率fD,傅里叶变换将所有向量旋转到相位φTx1 (l = 0),得到最大值
 (6)
(6)
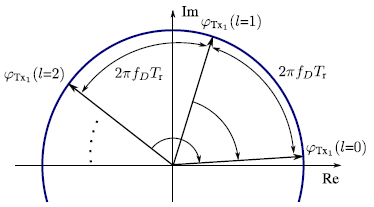
图2 在单发射机系统中,单个目标在两个连续chirp之间的相位差为2π fDTr。对于多普勒频率的提取,傅里叶变换将所有向量旋转到相位φTx1 (l = 0),用箭头表示。矢量的构造叠加导致频谱在fD处出现一个峰。
在TDM MIMO的情况下,存在第二个发射机Tx2。如图1所示,每次连续的chirp后,活动的发射机被切换。在不失一般性的前提下,假设φ = 0。图3显示了DFT如何将Tx2对应的所有向量变换为相位φTx2 (l = 0)。Tx1对应的所有向量的行为仍然如图2所示![]() 引入运动引起的系统误差φerr = 2π fDTr /2。
引入运动引起的系统误差φerr = 2π fDTr /2。
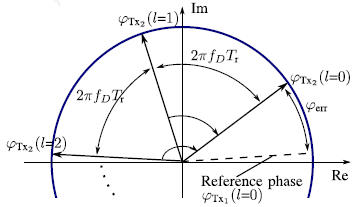
图3 在TDM MIMO雷达中,每个发射机的chirp都是独立处理的。当Tx1的DFT将所有相位转换为φTx1 (l = 0)时,Tx2的相位被转换为φTx2 (l = 0),这导致系统相位误差φerr = 2π fDTr /2。
为了减轻这种误差,改变多普勒处理。Tx1对应的chirp仍然用正常的DFT(6)进行处理。对于Tx2传输的chirp,DFT调整为
![]() (7)
(7)
通过这种稍微调整的DFT, Tx2的chirp相位也被转换为相位φTx1 (l = 0)。对于θ≠0,根据(1)将一个恒定相位添加到φTx2 (l)中。由于该相移与l无关,因此可以从(7)的和中提取。因此,所提出的处理对任何θ都有效。[10]中提出了一种减少多普勒模糊的相关处理方法。
将该方案推广到M个发射机,计算发射机Txm的多普勒DFT
![]() (8)
(8)
由于DFT的线性,(8)在多目标情况下也成立。注意,这种处理方式相当于在常规DFT处理之前在多普勒维中进行交错的零填充。这意味着对于Tx1传统DFT的输入是向量
![]() (9)
(9)
对于Tx2,它是
![]() (10)
(10)
3 仿真和测量
仿真比较了应用传统离散傅里叶变换(6)和改进的离散傅里叶变换(8)对运动目标的DoA估计与静态目标的DoA估计。仿真雷达采用表1中的参数,采用TDM MIMO阵列,其中两个发射机相距5λ,十个接收机间隔λ/2。它形成一个20元均匀线性虚拟阵列,阵元间距λ/2。所有的DoA估计都是用Bartlett波束形成器完成的[11]。
表1 仿真和测量的调制参数

在无噪声仿真中,假设目标距离为30m,θ=15°,速度为v = 0和v = 18m/s。图4显示了包含目标的距离-多普勒单元的DoA估计。v = 0的估计结果为15.2°,最接近15°的实际DoA。此估计用作参考。当v ≠ 0时,用(6)确定距离-多普勒频谱时,运动引起的相位误差使估计的DoA变为18.5°,导致频谱变形。然而,当使用(8)进行多普勒处理时,v = 18m/s的估计与静态参考相同。
测量评估是用一个TDM MIMO雷达进行的,该雷达有两个发射机和十个接收机,调制参数见表1。虚拟阵列是一个均匀的线性阵列,元件间距为0.545λ,包含一个重叠阵元。传感器安装在一辆速度约为18米/秒的汽车上。采用传统的DFT处理(6)和新提出的处理(8)计算距离-多普勒矩阵。在距离-多普勒频谱中选择一个明显的目标峰进行DoA估计。图5显示了该峰值在虚拟阵列位置处的相位。在位置10(重叠阵元),两个相位包含在图中。转换前的虚拟阵元属于第一发射机,其他虚元属于第二发射机。在重叠阵元位置,由于运动引起的相位误差,常规处理(6)存在1.54 rad的相位不连续。相位校正距离-多普勒处理(8)没有显示出如此严重的偏差。相反,重叠阵元位置处的相位值几乎相同。
图6给出了采用式(6)进行距离多普勒处理、采用式(6)进行距离多普勒处理并根据[6]进行重叠阵元相位校正、采用单个发射机数据[单输入多输出(SIMO)]进行距离多普勒估计、采用式(8)进行距离多普勒处理的几种情况对应的DoA估计。
(6)的应用导致DoA估计出现两个宽峰。总体最大值出现在DOA为1°处。当使用重叠阵元进行相位校正时,估计结果在3.9°处出现一个窄峰,曲线形状的旁瓣明显降低。SIMO估计孔径较小,分辨率较差;然而,4.3°DoA估计的最大值与之前的估计非常相似。用(8)进行距离多普勒处理后的MIMO DoA估计,估计DoA为3.9°,曲线形状与使用重叠阵元处理后的DoA估计基本一致;然而,它在虚拟孔径不需要重叠的阵元。

图4 不同速度v = 0和v = 18m/s下单个目标在15°方向上的仿真。当v = 0时,不发生相位误差。在v = 18m/s的情况下,用(6)进行多普勒处理,运动引起的相位误差会导致错误的DoA估计和频谱变形。经调整后的DFT(8)进行多普勒处理时,DoA估计与不考虑速度的DoA估计相同。

图5 在MIMO虚拟阵列的阵元测量相位。位置10的阵元在虚拟孔径中出现两次。
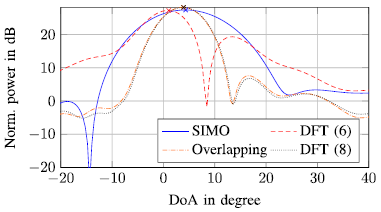
图6 测量为18m/s的DoA估计
4 结论
这篇文章介绍了一种距离-多普勒处理,以减轻TDM MIMO雷达中运动引起的相位误差,而无需额外的硬件努力,如重叠阵元。仿真结果表明,该处理方法在动态场景下的DoA估计性能与传统处理方法在静态场景下的DoA估计性能相同。测量结果也验证了运动引起的相位误差的补偿。
这篇关于论文解读--Compensation of Motion-Induced Phase Errors in TDM MIMO Radars的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





