浙江万里学院“真我风采”程序设计竞赛 ：四边形的面积

已知平面上四点P1、P2、P3、P4的坐标，分别为(X1,Y1)、(X2,Y2)、(X3,Y3)、(X4,Y4)
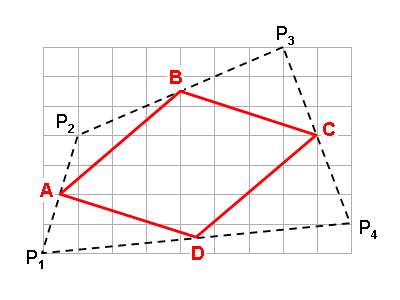
如果将P1P2连线的中点A、P2P3连线的中点B、P3P4连线的中点C以及P4P1连线的中点D连接为一个新的四边形，你能否计算出四边形ABCD的面积？

输入

P1、P2、P3、P4的坐标，每行两个值，横坐标在前，纵坐标在后，以空格分隔
每个坐标值均为整数，取值范围在[0,10000]之间，即：最小为0，最大为10000

输出

四边形ABCD的面积，保留两位小数

样例输入 Copy

0 0
1 4
7 7
9 1

样例输出 Copy

19.25

提示

在平面几何中，ABCD被定义为中点四边形。容易证明：ABCD为平行四边形

#include <stdio.h>
#include <math.h>
double Area(int x1, int y1, int x2, int y2, int x3, int y3, int x4, int y4);
int main() {int x1, y1, x2, y2, x3, y3, x4, y4;scanf("%d%d%d%d%d%d%d%d", &x1, &y1, &x2, &y2, &x3, &y3, &x4, &y4);printf("%.2f\n", Area(x1, y1, x2, y2, x3, y3, x4, y4));
}double Area(int x1, int y1, int x2, int y2, int x3, int y3, int x4, int y4) {double a, b, c, d, e, q, A, B = -1.0, C, area;double X1, Y1, X2, Y2, X3, Y3, X4, Y4;X1 = (x1 + x2) / 2.0;X2 = (x3 + x2) / 2.0;X3 = (x3 + x4) / 2.0;X4 = (x1 + x4) / 2.0;Y1 = (y1 + y2) / 2.0;Y2 = (y3 + y2) / 2.0;Y3 = (y3 + y4) / 2.0;Y4 = (y1 + y4) / 2.0;a = sqrt(pow(X1 - X2, 2.0) + pow(Y1 - Y2, 2.0));b = sqrt(pow(X2 - X3, 2.0) + pow(Y2 - Y3, 2.0));c = sqrt(pow(X1 - X3, 2.0) + pow(Y1 - Y3, 2.0));q = (a + b + c) / 2.0;e = sqrt(q * (q - a) * (q - b) * (q - c));area = 2.0 * e;return area;
}

海伦公式：S=sqrt(p(p-a)(p-b)(p-c))         p=(a+b+c)/2;

由题知，中点四边形是平行四边形，所以.......