本文主要是介绍王小草【机器学习】笔记--隐马尔可夫模型HMM,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
标签(空格分隔): 王小草机器学习笔记
机器学习的套路:
参数估计–>模型预测
隐马尔可夫模型需要涉及的步骤:
概率计算
参数估计
模型预测
应用:中文分词,语音识别等
在中文分词中,如果学习到了参数,隐马尔可夫就不需要词库也可以分词,但如果有词库,就会增加正确性。
所以在工业中可以HMM+词典来进行中文分词
但HMM可以发现新词,这个新词在词库中是没有的。
1. 什么是HMM
1.1 HMM初识
HMM可用于标注问题(词性标注),语音识别,NLP,生物信息,模式识别等领域。
HMM是关于时序的概率模型,描述由一个隐藏的马尔科夫链生成不可观测的状态随机序列,再由各个状态生成观测粹机序列的过程。
HMM随机生成的状态随机序列,称为状态序列;每个状态序列生成一个观测,由此产生的观测随机序列,称为观测序列。
隐马尔可夫模型的贝叶斯网络:
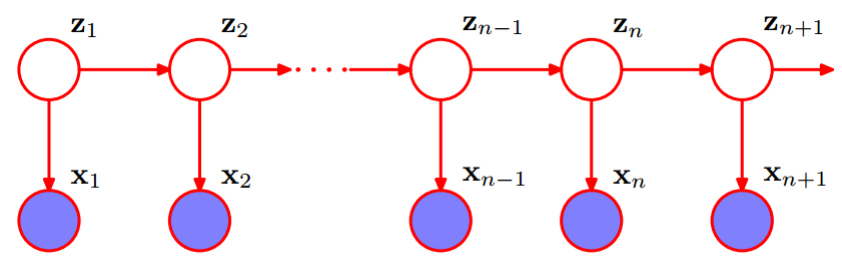
如上图中,第一行的z是一组不可观测的随机序列,即状态序列;下面一行x是可观测的随机序列,即观测序列。每一个位置可以看成是一个时刻,但这个时刻并不是严格意义上的时间,也可以是空间上的,比如DNA。
假设现在有一句话“隐马尔可夫模型的贝叶斯网络”。如果要分词的话我们希望是这样分“隐/马尔可夫/模型/的/贝叶斯/网络”。
要将这些词分出来,其实我们只需要知道哪个字是一个词语的终止字。比如“夫”,“型”,“的”,“斯”,“络”都是终止字,他们出现表示一个词语的结束。
一个字是不是终止字,我们叫做是这个字的隐状态,表示成(0,1),0表示非终止字,1表示是终止字。这个因状态就是上图中的z1,z2,z3….
现在中文分词的问题就转变为寻找一个字的隐状态的问题了。
在来看一个概念,如果有a,b,c三个点,a指向b,c。当我们不知道a的时候,我们说b,c是不独立的。
表示成公式可以这样:
当a不知道的时候,bc是不独立的p(c,b) ≠ p(c)p(b)
当a知道的时候,bc是独立的p(c,b/a) = p(c/a)p(b/a)
根据以上概念,再来看回上面的图。当z1不知道的时候,我们说x1和z2是不独立的。
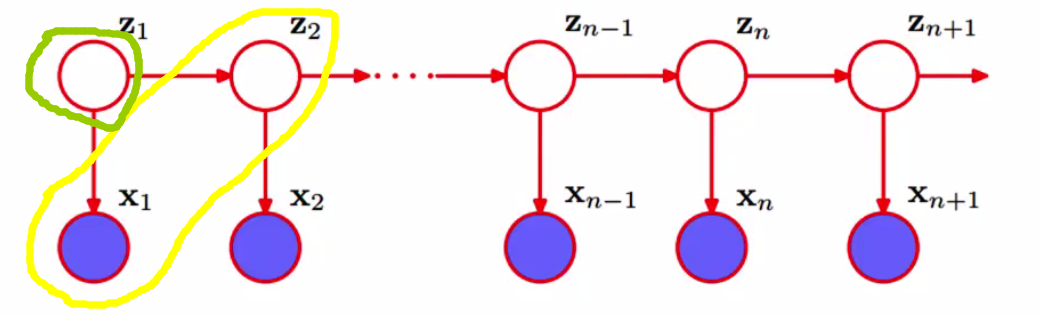
也可以说,当z1不知道的时候,x1和(z2,x2)是不独立的。
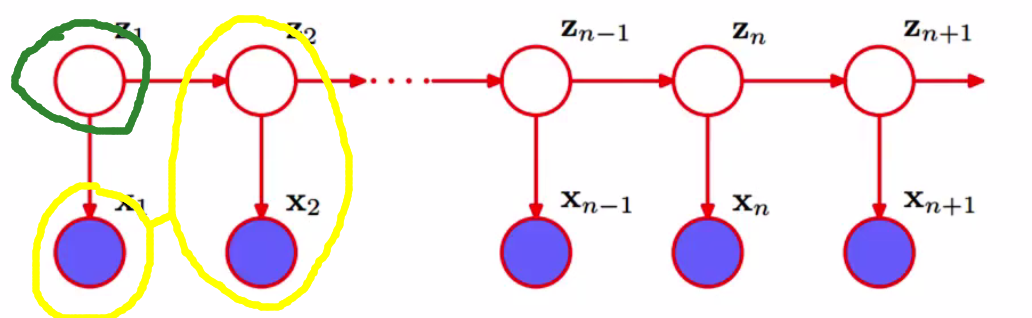
可以想见,对于一句话,前后的字之间总是相关的。
1.2 HMM的参数确定
1.2.1 参数的来源与原理
概率矩阵A
在中文分词中每个隐状态都是两种可能(0,1)。但是比如说预测天气,预测投骰子,很多问题都是说个可能的。我们假设如何情况下的隐状态有n中可能。(1,2,3…)
现在假设从z1到z2,z1有n中状态,z2也有n种状态,当z1是1的时候,z2可以是1,2,3…n;当z1是2的时候,z2可以是1,2,3…n;当zn是n的时候,z2可以是1,2,3…n.酱紫的话,我们可以用一个n*n的表格来表示出这种可能的关系。
| z1/z2 | 1 | 2 | 3 | 4 | … | n |
|---|---|---|---|---|---|---|
| 1 | a11 | a12 | a13 | a14 | … | a1n |
| 2 | a21 | a22 | a23 | a24 | … | a2n |
| 3 | … | … | … | … | … | … |
| … | … | … | … | … | … | … |
| n | an1 | an2 | … | … | … | ann |
aij表示的是由z1的n=1转换到z2的n=j的概率。比如a12表示z1的隐状态为1时,z2的隐状态为2的概率。于是这个n*n的矩阵我们称之为概率转换矩阵A。
既然是概率矩阵,那么当z1=1时, z2=1或2或3或..n的概率相加一定是等于1的。但是当z1=1,z2=1;z1=2,z2=1,…z1=n,z2=1的所有概率相加是不一定等于1的。也就是说,概率矩阵A的每行和都是1,每列的和不一定是1.这是概率矩阵的性质。
混淆矩阵B
上面讲了z1到z2的过程(前一个时刻到后一个时刻)。然而z1不止指向了z2,还指向了x1。
如果z的隐状态仍然是n个:1,2,3…n
这篇关于王小草【机器学习】笔记--隐马尔可夫模型HMM的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








