本文主要是介绍王小草【深度学习】笔记第三弹--神经网络细节与训练注意点,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
欢迎关注本人微信公众号:王小草之大数据人工智能。不定期分享学习笔记。
欢迎关注本人喜马拉雅账号:好吧我真的叫王草。不定期更新各类有声书与文章,涉及诗歌,自传日志,科技IT新书等。
恩,对,一名励志要做播主的爱好文学的经管专业的却打起代码的伪女程序猿,等你一起来聊聊哲学。
1. 权重的初始化
1.1 fine-tuning
神经网络的训练的有两种方式,第一种是自己从头到尾训练一遍;第二种是使用别人训练好的模型,然后根据自己的实际需求做改动与调整。后者我们叫做fine-tuning.
在model zoo有大量训练好的模型(不知道的可以百度一下model zoo)
fine-tuning相当于站在巨人的肩膀上,使用别人已经训练好了的优秀的模型去实现自己的需求。一般分为以下两种调整方式:
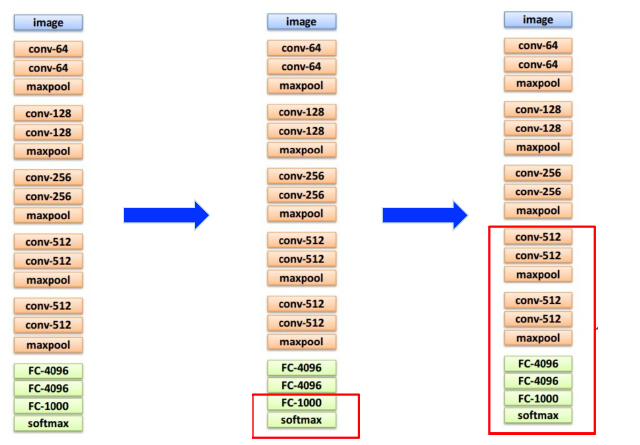
1.只修改FC(全连接层),比如原来的模型是1000个类别,而你实际上只需要分2个类别,那么你就可以调整FC的神经元个数与权重。并且设置前面所有没有改动的层的学习率为0,然后加大FC层的学习率。
2.包括了调整卷基层,激励层,池化层的神经元个数,或者减少或增加层级的数量。并且调低前面所有没有改动的层的学习率,然后加大后面层的学习率。这种方式的收敛更快和好。
1.2 随机数很小数初始化权重
在做逻辑回归时我们一般都将权重初始化为0,但是,在做神经网络的时候,权重如果很小或等于0,就会出现问题了。
假设权重为0,那么每个节点上的z = wx + b 这个线性函数运算结果都几乎为z = b。然后无论接下来使用什么类型的激励函数,这个函数的值y = g(z)在每个节点上都是相同的。也就是说BP的前向运算的时候得到的结果的是一样的,那么在反向传播时作用在每个权重的更新都是一致的,这绝必不是我们想要的。还记得上一个笔记中提到过,每个神经元会各自去负责一类特征(比如颜色,纹理等),只有在这个特征出现的时候,我们才希望对应的那个神经元被激活了。所以,正常情况下,每个神经元的输出应该是各不相同的。
下面做了一个实验,搭了一个10层的神经网络,并且设置w的初始值是一个很小很小的数,目的是想看看将w初始化成非常小的随机数会对神经网络的运作产生什么不好的影响?
下图10个蓝色的柱状图表示的是在过了激活函数后的每层神经元的输出结果的柱状图。每个柱状图是该层的所有神经元输出结果的一个分布图。蓝色的线形图是10层神经网络每层神经元输出结果的均值。旁边红色的线形图是每层的方差。
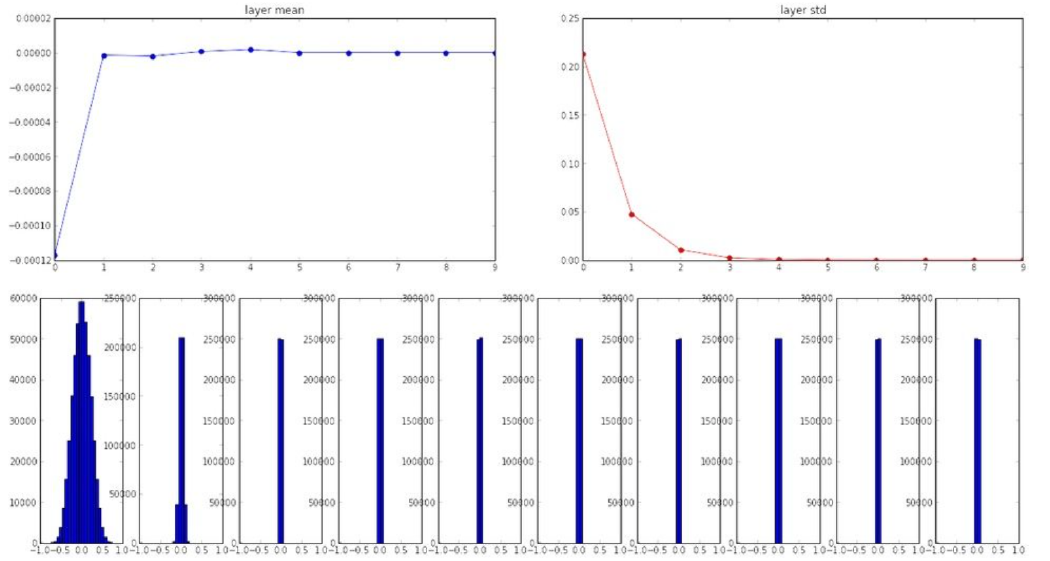
分析上图。当计算第一层的时候,均值很小,约为-0.000117,方差比较大约等于0.2,柱状图也显示,第一层的神经元的输出也是分布比较分散的,表示各个神经元的输出各异。
再看第二层。均值一下子上升到了-0.000001,而方差骤降到了0.04,从分布图看该层的神经元输出变得很集中,几乎都分布在一个很狭窄的范围内。也就是说,在第二层的时候,不同神经元的输出趋于一致了,他们的活力降低了。
接着看下面几层,均值小幅上升,方差继续下降,神经元的输出结果越来越一样,到第10层的时候方差已经为0 ,就是说所有神经元的输出都完全相等了。(哭脸)
上面这个实验我们可以得出一个结论:当权重的初始值非常小的时候,对于浅层的神经网络还勉强能够胜任,但是对于深层的神经网络就丧失了活力,这就是上个笔记中提到的“梯度弥散”现象。出现了“梯度弥散”,激励函数就从此挂掉,整个模型的训练也付之东流了。(再哭脸)
1.3 随机数较大数初始化权重
既然权重的初始化不能是很小的数,那么将权重设成比较大的数是否可以呢?
再来做一个实验,此时将权重设置为1。我们来看下面的结果图ÿ
这篇关于王小草【深度学习】笔记第三弹--神经网络细节与训练注意点的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




