现代密码学——Hill2密码算法的加、解密及破译 C语言代码实现

一、实验室名称：攻防实验室
二、实验项目名称：Hill2密码算法的破译
三、实验学时：2 学时
四、实验原理：
破译关键是求得加密矩阵的逆——解密矩阵。
分析出两个线性无关的明文向量与相应的密文向量，即可利用可逆矩阵求解矩阵方程计算出解密矩阵。即：

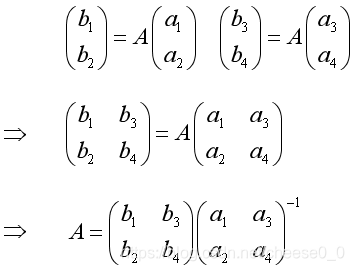
五、实验目的：
1、熟悉密码算法的基本破译方法；
2、理解密码算法破译中基于数学的分析方法的基本思路。
六、实验内容：
实现2阶Hill密码在已知明文攻击场景中，基于向量线性无关的破译。
七、实验器材（设备、元器件）：
学生每人一台PC，安装Windows 7操作系统及VC++/Python开发环境。
八、实验步骤：
1．密钥生成
Hill2密钥以一个二阶正整数值的矩阵作为加密矩阵。在这次实验中我使用和仿射密码一样的思路，一次一密，通过生成一个随机的二阶矩阵来作为密钥，每次加密都有不同的加密矩阵。
不过这些加密矩阵也是有条件的，由于HILL密码是对称密码，解密时需要用到加密矩阵的逆矩阵，所以加密矩阵A必须可逆。另外，我们假设要加密的明文是由26个字母所构成，每个明文字母与 0-25 的一个数字建立对应关系，所以所有运算都是在mod 26下进行的。我使用C语言中的do while结构通过规约二阶随机矩阵来产生合适的加密矩阵。矩阵可逆的条件是矩阵的行列式与26是互素，这部分代码如下：

do{matrix[0][0]=rand()%26;matrix[0][1]=rand()%26;matrix[1][0]=rand()%26;matrix[1][1]=rand()%26;dt = -1;for(p=1; dt < 0; p++){dt = ((matrix[0][0] * matrix[1][1] - matrix[0][1] * matrix[1][0]) + 26 * p)%26; //行列式的值 }
}while(gcd(dt,26)!=1); 

2. 加密
由于加密需要将明文字母依次按每两个字母一组查出其表值，形成二维向量，而实际应用中，明文不一定为偶数个，当明文为奇数时，需要对明文添加补位。在算法实现中，我先判断明文字符串的个数，当它不能整除2时，在末尾添加一个字母，例如“a”。在明文字符为奇数个时，加密完成后，在命令行输出密文时，我去掉了末尾的补位，但是为了便于后续解密工作，我在输出密文文件中保留了末位。

if(len % 2 == 1) {pla[len] = 'a';len = len+1;flag = 1;}

对于大小写的问题，在仿射密码时，我是将大小写区分开进行加密解密。但是本次实验相对复杂，需要两个字母组成一组向量进行加密，在mod 26的情况下大小写区分加密无法实现。所以在这里，我将明文大写字母转化为小写字母后再进行加密。将大写转成小写，并赋值给tran1数组，该数组是int型的数组，存放的是输入明文字母对应的表值。这里规定a-z每个字母与0-25这26个数字形成一一对应关系，形成表值。

 for(i=0; i<len; i++){if(pla[i] >= 'A' && pla[i] <= 'Z'){pla[i] = pla[i] + 32;}tran1[i] = pla[i] - 'a';}

将生成的合乎条件的二阶正整数矩阵作为加密矩阵，将明文字母依次按每两个字母一组查出其表值，通过查表将明文字母转化为一组二维向量，设加密矩阵为A，则通过加密矩阵加密，得到，查向量的字母表值，得到密文字母。实现加密部分算法如下。

for(i=0; i<len; i=i+2){T1[0] = tran1[i];T1[1] = tran1[i + 1];// cip存储密文int//加密 cip[0] = (T1[0] *matrix[0][0] + T1[1] * matrix[0][1]) % 26;cip[1] = (T1[0] *matrix[1][0] + T1[1] * matrix[1][1]) % 26;s[i] = cip[0];s[i + 1] = cip[1];}for(i=0; i<len; i++)ciph[i] = s[i] + 'a';   

3. 解密
解密时的密钥是需要手动输入的，是考虑到等待解密的密文可能不是由上一个加密矩阵加密得到的密文。
如果仅仅是对本程序加密得到的密文解密，那不必考虑密文字母的个数和大小写问题，因为加密过程中输出的密文文件中的字母一定是小写而个数一定是偶数个，但是如果对于外来的文件进行解密，可能存在大小写不一致和个数为奇数个的情况，所以我在解密过程中也考虑了奇数个字符串进行补位和将大写转化为小写的步骤，与加密过程相似。在这里对奇数个字符串进行补位时要注意得到解密后的明文的末位只有1/26的概率是对的，因为我们不知道奇数个密文的原来的那个被去掉的补位的值，所以此时的补位并不能保证是原有的那个字符。而解密也需要两个字符为一组，将其一起进行解密，这样所得的结果才正确。
利用加密矩阵的逆矩阵，通过就可以由密文得到明文。解密的关键就是得到加密矩阵A的逆矩阵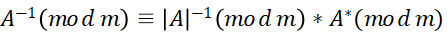，其中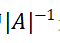是矩阵A的行列式在模26下的逆元，是矩阵A的伴随矩阵。因为矩阵A是二阶矩阵，其伴随矩阵也比较容易得出：主对角线元素互换，副对角线元素加负号。

//求矩阵的逆det = -1;for(i=1; det < 0; i++){det = ((matrix1[0][0] * matrix1[1][1] - matrix1[0][1] * matrix1[1][0]) + 26 * i)%26;}i = 1;while(1){if((det * i) % 26 == 1){invdet = i;break;}elsei++;//逆矩阵matrix2[0][0]=(matrix1[1][1]*invdet)%26;matrix2[0][1]=(((-1 * matrix1[0][1]) + 26) * invdet) % 26;matrix2[1][0]=(((-1 * matrix1[1][0]) + 26) * invdet) % 26;matrix2[1][1]=(matrix1[0][0]*invdet)%26;// 得到解密后结果for(i=0; i<len; i+=2){T1[0] = tran1[i];T1[1] = tran1[i + 1];// msg存储明文int值msg[0] = (T1[0] * matrix2[0][0] + T1[1] * matrix2[0][1]) % 26;msg[1] = (T1[0] * matrix2[1][0] + T1[1] * matrix2[1][1]) % 26;mes[i] = msg[0];mes[i + 1] = msg[1];}

解密过程就是加密的逆过程，代码实现也类似。
4. 已知明文攻击原理
假设我们知道了明文中的四个字母对应的密文，假设得到明文字母的表值为a1、a2、a3、a4，而对应的密文字母表值为b1、b2、b3、b4。根据加密的算法可以知道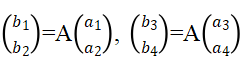，也就是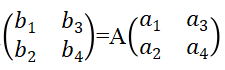，我们知道了两个线性无关的明文向量与相应的密文向量，我们就可以求出加密矩阵或者加密矩阵的逆矩阵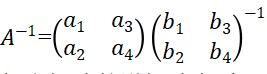，有了加密矩阵的逆矩阵，要恢复出明文，只需要用加密矩阵的逆矩阵左乘上密文向量，即可以破译HILL密码。
也就是只要我们得到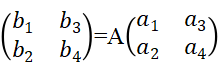，并由此可以解出加密矩阵，剩下的就和解密算法一样了。
九、实验数据及结果分析：
1．实验参考代码：
1.Hill2.c Hill2的加密算法与解密算法的实现

2.CrackHill.c 已知明文攻击

完整代码请移步资源区下载

2.加密及解密实例结果截图：
待加密明文：plain.txt

加密及解密：

已知明文攻击：
密文c.txt


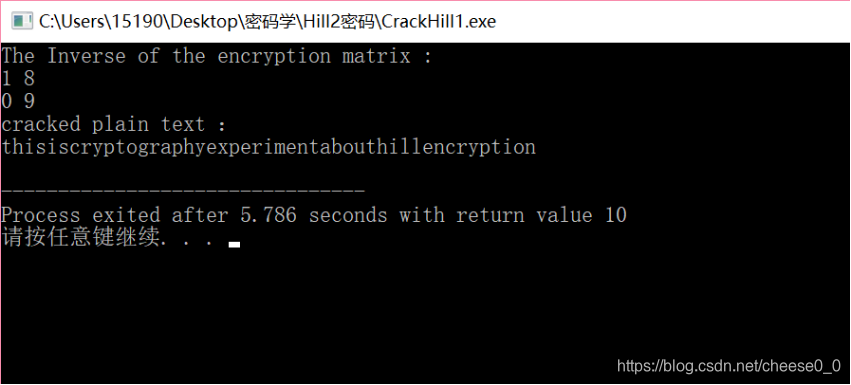
十、实验结论：
本次实验实现了Hill2密码的加密和解密算法，并进行了已知明文攻击。这次实验让我第一次尝试将矩阵在C语言中应用，也让我熟悉了关于Hill2算法的理论知识，并付诸实践实验。在理论和实践中对Hill2密码算法进行了更深刻的理解和掌握，通过一个个实验逐步将理论知识运用到实际工程中。
十一、总结及心得体会：
解密这部分算法让我纠结很久，因为我想让程序更具有实用性。如果仅仅是将前面加密得到的密文文件解密，那这个密文一定是偶数个的，我就无需考虑奇数个密文的情况。但是考虑到实用性，我想随手拿来一段密文都可以实现解密，这就要对密文的奇数偶数个进行讨论，所以我在解密部分代码中也对奇数个密文的情况进行了分析。还有一个让我很纠结的地方，对于解密后密文的输出，因为我考虑了外来密文解密的情况，如果是偶数则直接输出，如果是奇数，则在输出时去掉末尾的补位（其实去掉只是为了和原明文长度一致，并无其他意义），而且会因为不知道原密文的末尾字母，而导致最后一位解密出错，因为hill2密码的实现就是两个为一组一起加密，将他们单独看是毫无意义的。但是由于在加密时，我将加密的密文文件直接给了后续解密，这里没有去掉最后一位，所以此时，接受的密文字母一定是偶数个，这样明文字母实际有奇数个的情况就无法体现，在最后的输出时就不能判断是否去掉最后一位。所以在最后我也没有想到合适的方法来解决这个问题，就按照先对明文加密，再对所得密文解密验证正确性的流程来进行，没有将加密和解密流程独立开。
本次实验让我对hill2密码的加密和解密以及已知明文攻击的原理以及算法有了较深入的了解，通过编程语言来实现的过程也锻炼了我的实践能力和逻辑思维能力，让思维更加严谨清晰。
十二、对本实验过程及方法、手段的改进建议：
我认为我可以将加密部分和解密部分的代码写在子函数里，让主函数跟简洁明了，也可以让整个代码显得清晰明畅。
另外，在最后我没有顾及到程序的实用性，加密与解密没有完全独立开运行，解密独立使用时奇数个字母的密文解密所得明文的末位可能会存在不可避免的错误，这都是需要改进的地方。

报告评分：
指导教师签字：