本文主要是介绍【TripletTracking(ECCV2018)】论文阅读 Triplet Loss in Siamese Network for Object Tracking,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Triplet Loss in Siamese Network for Object Tracking 项目主页
写在前面
这篇文章发表在ECCV2018上,速度快,精度还行,但是个人感觉还是因为方法比较新才被接收的。这篇文章的思路其实很简单,很大的篇幅都是在解释triplet loss为什么管用,在这里就不详细描述这块内容,主要掌握一下思路,具体的公式以及可视化的比较可以去看论文。
Motivation
- 一个动机是使用Siamese的动机,那些需要在线更新的tracker十分费时,所以才要用这种realtime的结构;
- 另一个动机是本文是出发点:SiamFC虽然使用了比较好的特征,但是它没有充分利用样本直接的联系。
Contribution
- 将三元组损失引入到SiamFC中,使得tracker更加具有分辨力;
- 做了充分的公式推导,严谨得通过理论证明了为什么引入三元组损失管用
Algorithm
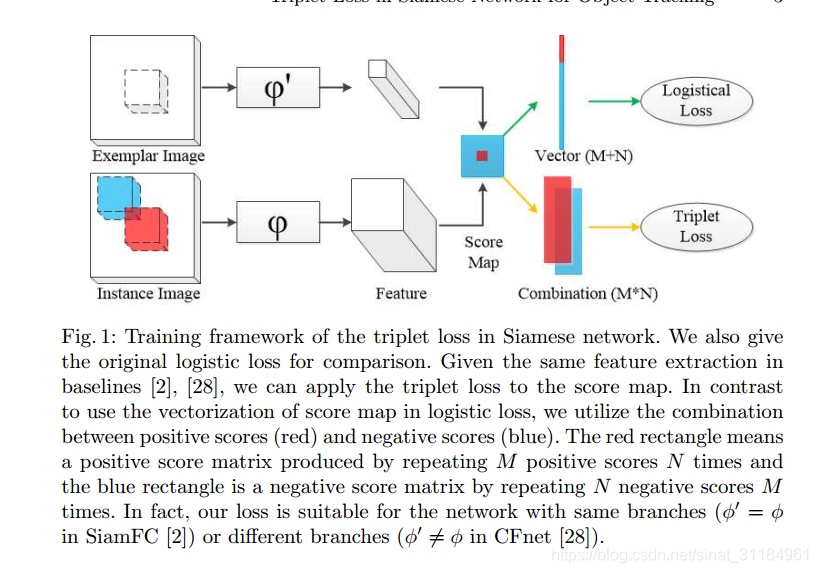
网络结构如上图,其实和SiamFC就是一样的,文章还特意把SiamFC使用的logistical损失也画了出来,从上图中也可以看到,logistical的损失一共有M+N中,这里的M是指正样本对,N是指负样本对的个数。也就是Triplet的损失一共有M×N种,而logistical的损失只有M+N中,这样的话肯定是Triplet利用到的信息更多。这个文章的网络结构和参数都和SiamFC一样,只是最后在损失函数上有了改变,所以速度和SiamFC几乎是一样的。
下面对比两个损失函数:
1、Logistical
L l ( Y , V ) = ∑ x i ∈ X w i l o g ( 1 + e − y i ⋅ v i ) L_l(Y,V) = \sum_{x_i \in X}w_ilog(1+e^{-y_i\cdot v_i}) Ll(Y,V)=xi∈X∑wilog(1+e−yi⋅vi)
2、Triplet
L t ( V p , V n ) = − 1 M N ∑ i M ∑ j N l o g ( e v p i e v p i + e v n j ) L_t(V_p,V_n) = -\frac{1}{MN}\sum_{i}^M\sum_j^Nlog(\frac{e^{vp_i}}{e^{vp_i}+e^{vn_j}}) Lt(Vp,Vn)=−MN1i∑Mj∑Nlog(evpi+evnjevpi)
其中Y表示ground truth, V表示样本 , V p V_p Vp表示正样本对, V n V_n Vn表示负样本对。
从两个损失函数中,我们也可以看出不同,第一个只是单纯的使用正样本对和负样本对,而第二个损失函数,正样本和负样本之间是有关系的,这样就充分利用了样本之间的一些联系。
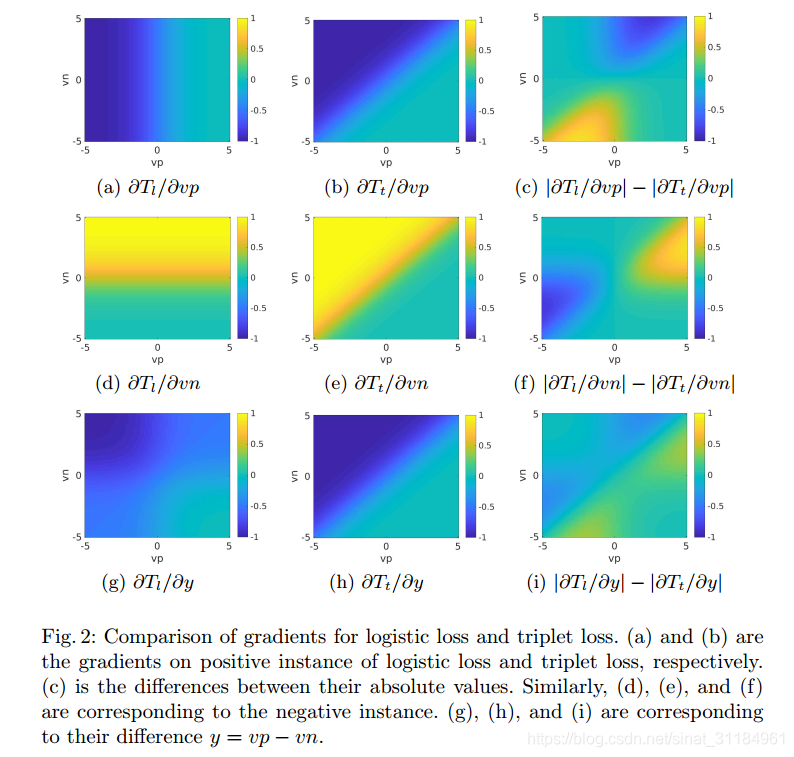
这么做的意义就是希望当 v p < v n v_p <v_n vp<vn的时候,损失函数给出的梯度大,也就是强调了需要优化的地方。 文章中有一节是对比两个损失的梯度变化的,对这个做了详细的解释,感兴趣的可以去看文章。
Experiment
这是对比梯度的实验。
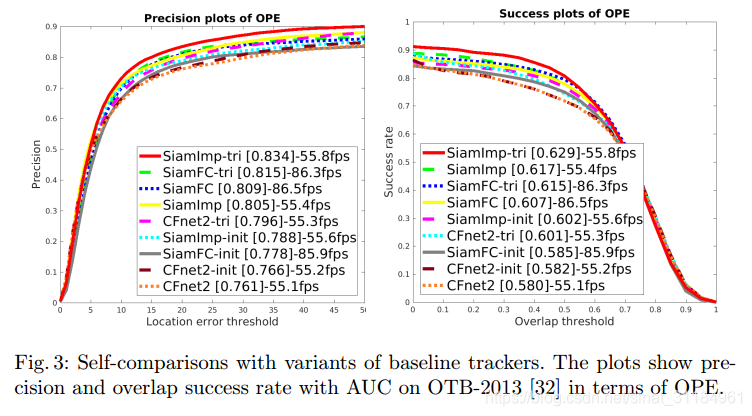
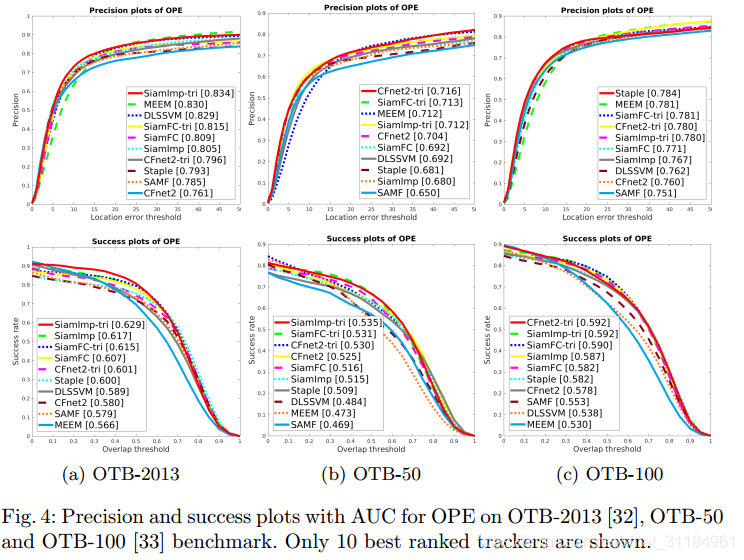

总结
优点
- 将三元组损失引入到SiamFC网络,使用的输入还是原始输入,特征提取过程都与SiamFC一样,只是在损失函数上面做了优化,但是在文章中试的三个tracker上效果都有提升;
- 有很完善的证明过程,也做了可视化的对比,有比较扎实的理论基础。
缺点
- 缺点的话就是SiamFC的一些缺点了吧,没有bbox回归,只在固定的search region里面搜索,目标reappear就不行了;
- 相似性检测的方法可能对目标的表观变化比较敏感,缺少模板更新;
- etc
这篇关于【TripletTracking(ECCV2018)】论文阅读 Triplet Loss in Siamese Network for Object Tracking的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







