[基本功]决策树

本文主要是介绍[基本功]决策树，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

决策树

什么时候结束划分？

• 当前结点包含的样本全属于同一类别，无需划分
• 当前属性值为空，或是所有样本在所有属性上取值相同，无法划分
• 当前结点包含的样本集合为空，不能划分

如何选择最优划分属性？

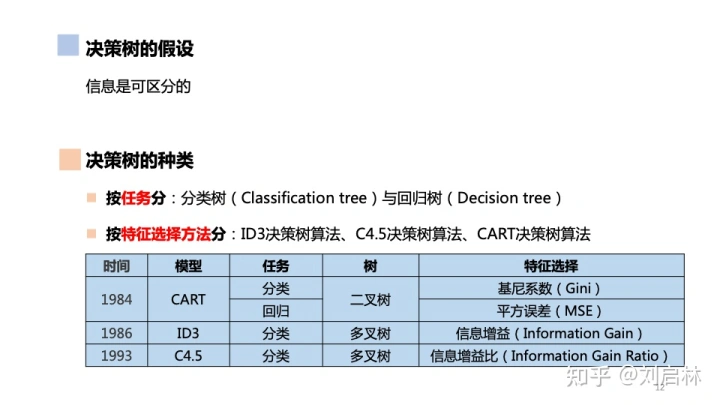
• 信息增益（ID3）

  • 信息熵，可以度量样本集合纯度

  $$Ent(D)=-\sum _{k=1}^{|y|}{p}_{k}lo{g}_2{p}_k$$

  • 熵越小，则D的纯度越高

  • 用A属性对D样本集合进行划分，得到的信息增益为：
  • 信息增益准则对可取值数目较多的属性有所偏好（比如ID，一人一个）
  • 【必须离散属性，多叉树或二叉树】

• 增益率（C4.5）

  • 增益率准则对可取值数目较少的属性有所偏好，因此C4.5并不是直接选择增益率最大的候选划分属性，而是使用了一个启发式：先从候选划分属性中找出信息增益高于平均水平的属性。再从中选择增益率最高的。
  • 【可连续可离散，多叉树或二叉树】

• 基尼指数（CART）

  • 分类和回归都可用

    • 数据集D的基尼值：

    $$Gini(p)=\sum _{k=1}^K{p}_k(1-p_k)=1-\sum _{k=1}^K{p}_k^2(越大越不纯)$$

    • 属性A的基尼指数：
      $$Gini\_index(D,a)=\sum _{v=1}^V\frac{|D^v|}{|D|}Gini(D^v)$$

    • 选最小的

  • 【可连续可离散，必须二叉树】

如何剪枝？

• 剪枝可以防止决策树过拟合，提高泛化性能

  • 预剪枝，若当前节点的划分不能带来泛化性能提升，则停止划分并将当前结点标记为叶结点

    • 优点：降低了过拟合风险，显著减少训练时间开销和测试时间开销

    • 缺点：有些分支当前划分虽不能提升泛化性能，但在其基础上的后续划分却有可能导致性能显著提高，预剪枝基于贪心本质，带来了欠拟合风险

  • 后剪枝，生成决策树后，自底向上对非叶节点考察，用单一叶结点代替整个子树

    • 优点：欠拟合风险很小，泛化性能往往优于预剪枝决策树
    • 缺点：训练时间开销比未剪枝决策树和预剪枝决策树大很多

其他

• 连续值处理

  • C4.5：二分法

  • 对连续属性a，可考察包含n-1个元素的候选划分点集合
    T a = { a i + a i + 1 2 ∣ 1 < = i < = n − 1 } T_a=\{\frac{a_i+a_{i+1}}2|1<=i<=n-1\} Ta​={2ai​+ai+1​​∣1<=i<=n−1}

  • 与离散属性不同，若当前结点划分属性为连续属性，该属性还可作为其后代结点的划分属性

• 缺失值处理

  • C4.5有自己的一套处理缺失值的方法

• 噪音数据可能影响决策树，在数据带有噪声的情况下，通过剪枝可将决策树的泛化性能提高25%

• 多变量决策树

  • 非叶节点不再是仅对某个属性，而是对属性的线性组合进行测试

这篇关于[基本功]决策树的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---