本文主要是介绍Peter算法小课堂—简单建模(4),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
太戈编程1655题
一条直线上,你安排了n个哨兵站岗放哨,编号从1到n。其中i号哨兵的坐标位置是x[i]。不会有哨兵站在相同的位置。作为指挥官,你需要知道3个信息:
1.从左到右,每个哨兵的坐标依次是几?
2.从左到右,每个哨兵依次是几号哨兵?
3.哨兵编号从1到n,每个哨兵依次站在从左到右的第几个?
离散化
什么是离散化呢?数据离散化处理_哔哩哔哩_bilibili
给出一列数字,在有些情况下,这些数字的值的绝对大小并不重要,而相对大小很重要。例如,对一个班级学生的成绩进行排名,此时不关心成绩的绝对值,只需要输出排名,如分数为{95,50,72,21},排名为{1,3,2,4}。
“离散化”就是用数字的相对值替代它们的绝对值。离散化是一种数据处理的技巧,它把分布广而稀疏的数据转换为密集分布,从而能让算法更快速、更省空间的处理。步骤:1.排序 2.离散化 3.归位
离散化手工编码:
#include <bits/stdc++.h>
using namespace std;
const int N=500010;
struct data{int val;int id;
}olda[N];
int newa[N];
bool cmp(data x,data y){return x.val<y.val;
}
int main(){int n;cin>>n;for(int i=1;i<=n;i++){cin>>olda[i].val;olda[i].id=i;}sort(olda+1,olda+1+n,cmp);for(int i=1;i<=n;i++){newa[olda[i].id]=i;}for(int i=1;i<=n;i++) cout<<newa[i];return 0;
}那么,回到1655,这题应该怎么做呢?
#include <bits/stdc++.h>
using namespace std;
const int N=100009;
int rk[N];
struct guard{//结构体int x,id;
};
guard g[N];
bool cmp(const guard&u,const guard&v){//排序return u.x<v.x;
}
int main()
{freopen("guard.in","r",stdin);freopen("guard.out","w",stdout);int n;cin>>n; for(int i=1;i<=n;i++) cin>>g[i].x;for(int i=1;i<=n;i++) g[i].id=i;//学号赋值sort(g+1,g+1+n,cmp);for(int i=1;i<=n;i++) rk[g[i].id]=i;for(int i=1;i<=n-1;i++) cout<<g[i].x<<" ";cout<<g[n].x<<endl; for(int i=1;i<=n-1;i++) cout<<g[i].id<<" ";cout<<g[n].id<<endl; for(int i=1;i<=n-1;i++) cout<<rk[i]<<" "; cout<<rk[n]<<endl;return 0;
}太戈编程56题
某校大门外长度为L的马路上有一排树,每两棵相邻的树之间的间隔都是1米。我们可以把马路看成一个数轴,马路的一端在数轴0的位置,另一端在L的位置;数轴上的每个整数点,即0,1,2,……,L,都种有一棵树 由于马路上有一些区域要用来建地铁。这些区域用它们在数轴上的起始点和终止点表示。已知任一区域的起始点和终止点的坐标都是整数,区域之间可能有重合的部分。现在要把这些区域中的树(包括区域端点处的两棵树)移走。你的任务是计算将这些树都移走后,马路上还有多少棵树
差分
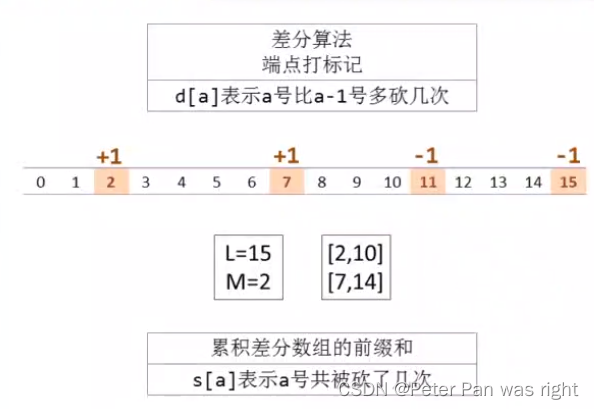
cin>>l>>m;
for(int i=1;i<=m;i++){cin>>a>>b;if(a>b) swap(a,b);a++;b++;//确保都为正整数d[a]++;d[b+1]--;
}那么,第5行我为什么敢无缘无故+1呢?这都是缓冲格的帮助。
然后呢?
#include <bits/stdc++.h>
using namespace std;
const int N=1000009;
int l,m,a,b,s[N],d[N];
int main(){freopen("tree.in","r",stdin);freopen("tree.out","w",stdout);cin>>l>>m;for(int i=1;i<=m;i++){cin>>a>>b;if(a>b) swap(a,b);a++;b++;d[a]++;d[b+1]--;}int ans=l+1;for(int i=1;i<=l+1;i++){s[i]=s[i-1]+d[i];if(s[i]) ans--;}cout<<ans<<endl;return 0;
}但是……如果303题怎么办呢?
太戈编程303题
#include <bits/stdc++.h>
using namespace std;
const int M=1000000009;
struct pnt{int x,tag;
}p[M];
bool cmp(const int&a,const int&b){if(p[a].x<p[b].x) return 1;if(p[a].x>p[b].x) return 0;if(p[a].tag<p[b].tag) return 1;return 0;
}
int main(){int l,m;cin>>l>>m;for(int i=1;i<=m;i++){int a,b;cin>>a>>b;if(a>b) swap(a,b);a++;b++;p[i].x=a;p[i].tag=1;p[i+m].x=b+1;p[i+m].tag=-1;}for(int i=1;i<=2*m;i++) id[i]=i;sort(id+1,id+1+2*m,cmp);int ans=l+1,pre=0;for(int i=1;i<=2*m;i++){if(s[i-1]) ans-=p[id[i]].x-pre;pre=p[id[i]].x;s[i]=s[i-1]+p[id[i]].tag;}cout<<ans<<endl;
}希望这些对大家有用,三连必回
这篇关于Peter算法小课堂—简单建模(4)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




