____________________________我往前飞 飞过一片时间海
1.
关于同余式的约去法则：
给出一个正整数m和三个整数a, b和c，d=GCD(c, m)，并且ac≡bc(mod m)。则a≡b(mod (m DIV d))。
2.___________________________________大数用于是被其因子这些小数整除的！
我们已经定义了两个数 a 和 b 的最大公约数 (a,b) .关于这个数有一个简单的公式 | （a，b) = GCD(a,b)!
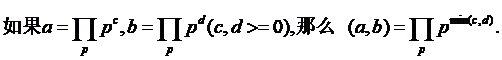
这是 min(c,d) 鸭子！
两个整数 a和b 的最小公倍数(least common multiple ) 是同时能被 a和 b整除的最小整数.用{a,b}表示。
于是有： a|{a,b} , b|{a,b}
在上述的记号的情况下，有：
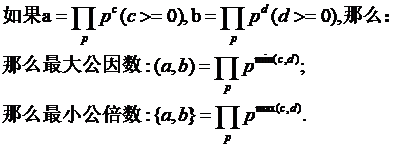图有些糊了，嘻嘻：
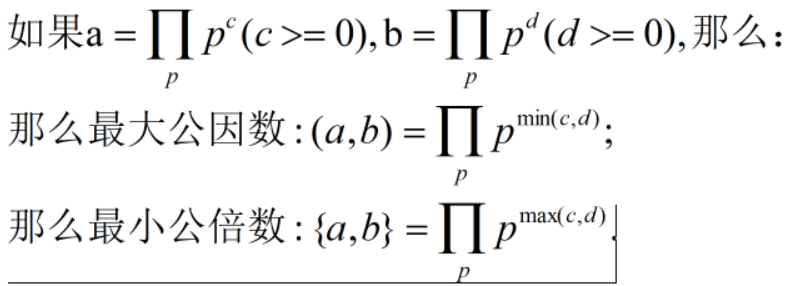
究极总结：
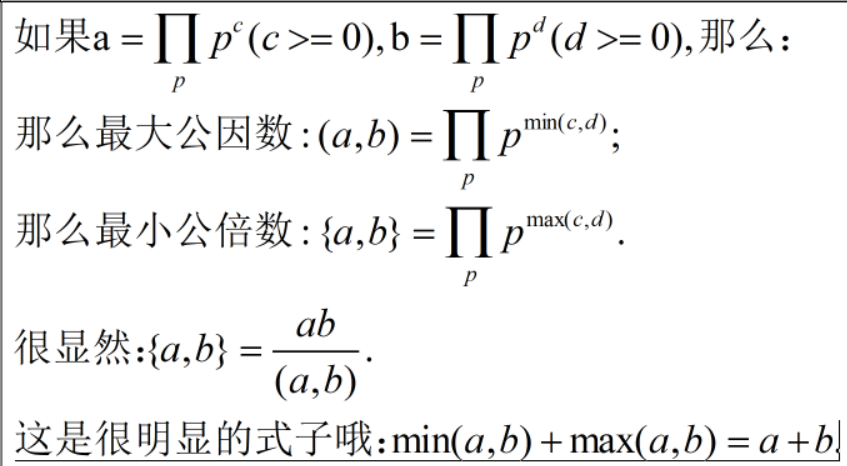
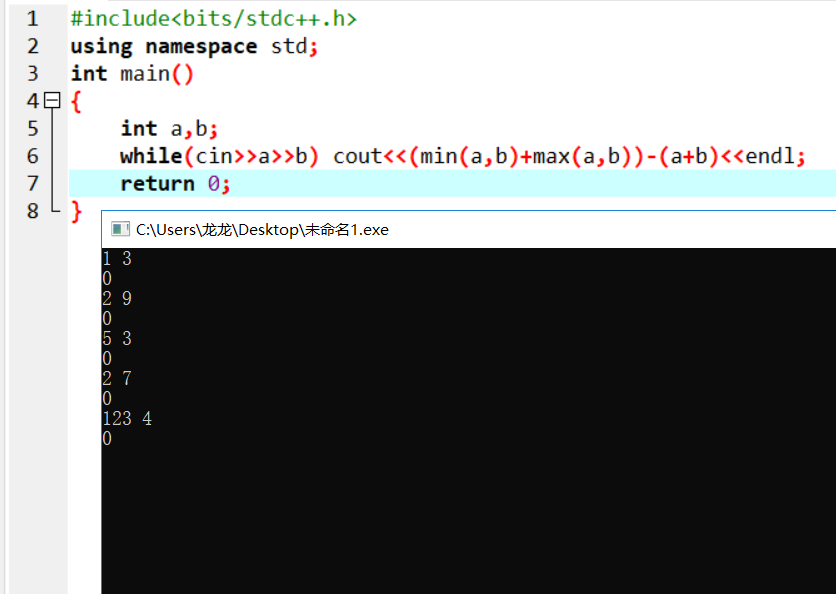
3.
4.有所待：https://vjudge.net/contest/316798#problem/C
codes:
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
ll pow_mod(ll a,ll p,ll M)
{if(p==0) return 1;ll ans=pow_mod(a,p/2,M);ans=ans*ans%M;if(p%2==1) ans=ans*a%M;return ans;
}
int main()
{int t,h;ll M;cin>>t;while(t--){cin>>M>>h;ll a,b,ans=0;while(h--){cin>>a>>b;ans=(ans+pow_mod(a,b,M))%M;}cout<<ans<<endl;}return 0;
}
观览书籍：
《哈代数论》
