算法通关第十九关-青铜挑战理解动态规划

本文主要是介绍算法通关第十九关-青铜挑战理解动态规划，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

大家好我是苏麟 , 今天聊聊动态规划 .

动态规划是最热门、最重要的算法思想之一，在面试中大量出现，而且题目整体都偏难一些对于大部人来说，最大的问题是不知道动态规划到底是怎么回事。很多人看教程等，都被里面的状态子问题、状态转移方程等等劝退了。
其实，所谓的状态就是一个数组，动态规划里的状态转移方程就是更新这个数组的方法。这一关，我们先理解动态规划到底怎么回事。

热身 : 斐波那契数列

首先来感受一下什么是重复计算和记忆化搜索。

public class FibonacciTest {public static int count = 0;public static void main(String[] args) {fibonacci(20);System.out.println("count:" + count);}public static int fibonacci(int n) {System.out.println("斐波那契数列");count++;if (n == 0) {return 1;}if (n == 1 || n == 2)return n;else {return fibonacci(n - 1) + fibonacci(n - 2);}}
}

这个就是斐波那契数列，当n为20时，count是21891次。而当n=30 的时候结果是2692537，也就是接270万。如果纯粹只是算斐波那契数列，我们可以直接循环:

    public static int count_2 = 0;public int fibonacci(int n) {if (n <= 2) {count_2++;return n;}int f1 = 1;int f2 = 2;int sum = 0;for (int i = 3; i <= n; i++) {count_2++;sum = f1 + f2;f1 = f2;f2 = sum;}return sum;}

n为30时也不过计算二十几个数的累加，但是为什么采用递归竟然高达270万呢?
因为里面存在大量的重复计算，数越大，重复越多。例如当n=10的时候，我们看下面的结构图就已经有很多重复计算了:

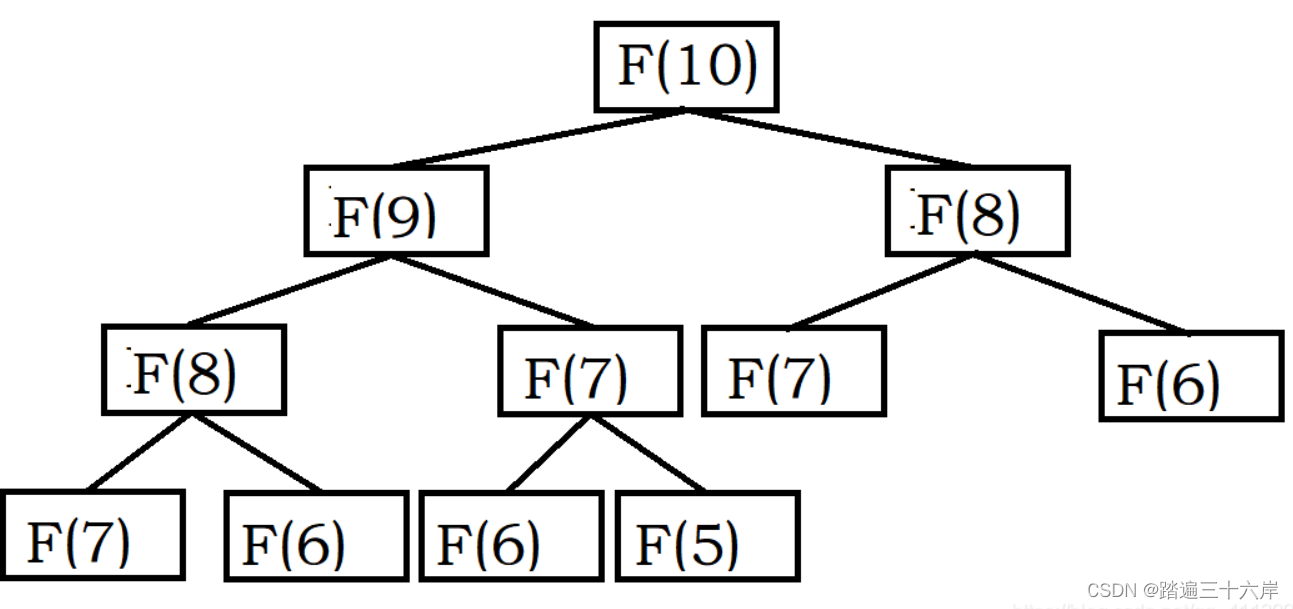
上面我们在计算f(10)时，可以看到f(9)、f(8)等等都需要计算，这就是重叠子问题。怎么对其优化一下呢?
可以看到这里主要的问题是很多数据都会频繁计算，如果将计算的结果保存到一个一维数组里。把 n 作为我们的数组下标，f(n)作为值，也就是 arr[n] = f(n)。执行的时候如果某人位置已经被计算出来了就更新对应位置的数组值，例如 f(4)算完了，就将其保存到arr[4]中，当后面再次要计算 f(4) 的时候，我们判断f(4)已经计算过，因此直接读取 f(4) 的值，不再递归计算。代码如下:

        public static int[] arr = new int[50];public static int count_3 = 0;Arrays.fill(arr, -1);arr[0] = 1;int fibonacci ( int n){if (n == 2 || n == 1) {count_3++;arr[n] = n;return n;}if (arr[n] != -1) {count_3++;return arr[n];} else {count_3++;arr[n] = fibonacci(n - 1) + fibonacci(n - 2);return arr[n];}}

在上面代码里，在执行递归之前先查数组看是否被计算过，如果重复计算了，就直接读取，这就叫”记忆化搜索“，就这么简单。

路径连环问题

基本问题 : 统计路径总数

描述 :

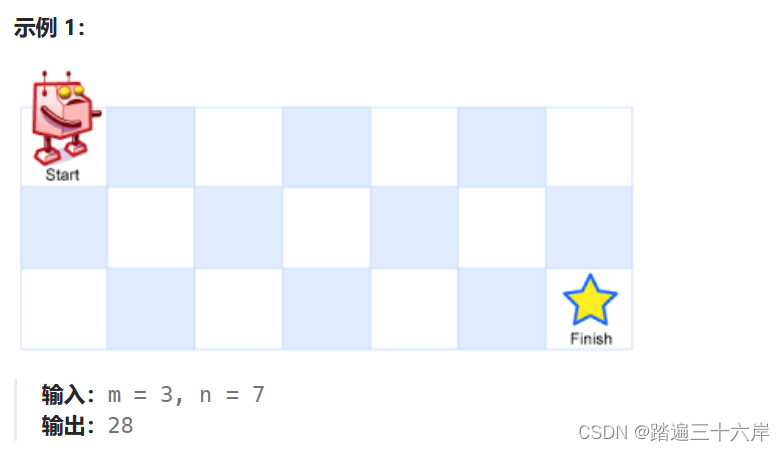
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

题目 :

LeetCode 62. 不同路径 :

不同路径

分析 :

我们先从一个3x2的情况来分析:

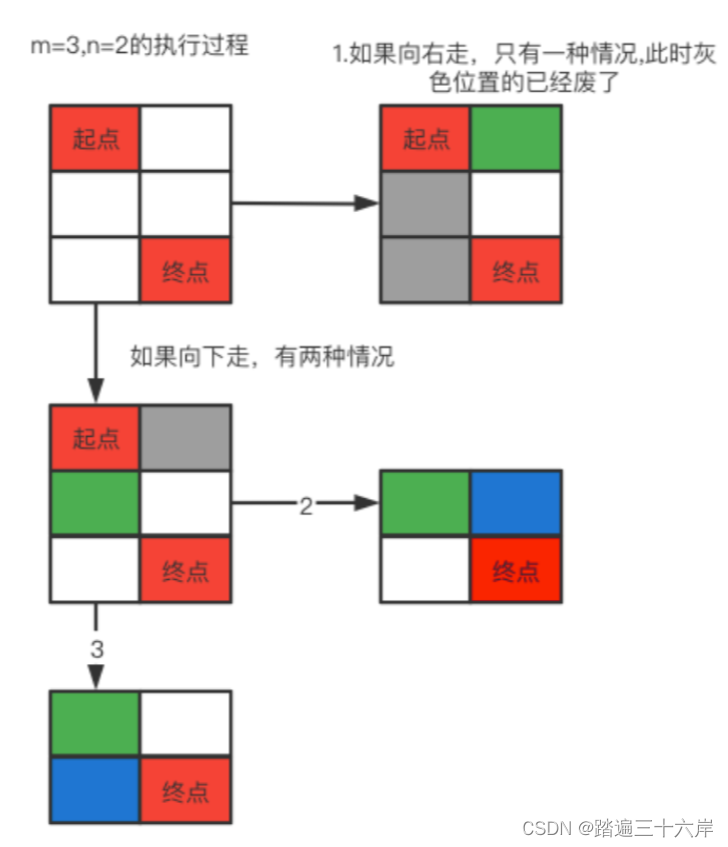
我们的目标是从起点到终点，因为只能向右或者向下，从图中可以可以看到:

1.如果向右走，也就是图1的情况，后面是一个3x1的矩阵，此时起点下面的两个灰色位置就不会再访问了，只能从绿色位置一直向下走，只有一种路径。

2.如果是向下走，我们可以看到原始起点右侧的就不能再访问了，而剩下的又是一个2X2的矩阵，也就是从图中绿色位置到红色位置，此时仍然可以选择向右或者向下，一共有两种路径。

所以上面的情况加起来就是一共有3种。

我们再看一下3X3的 :

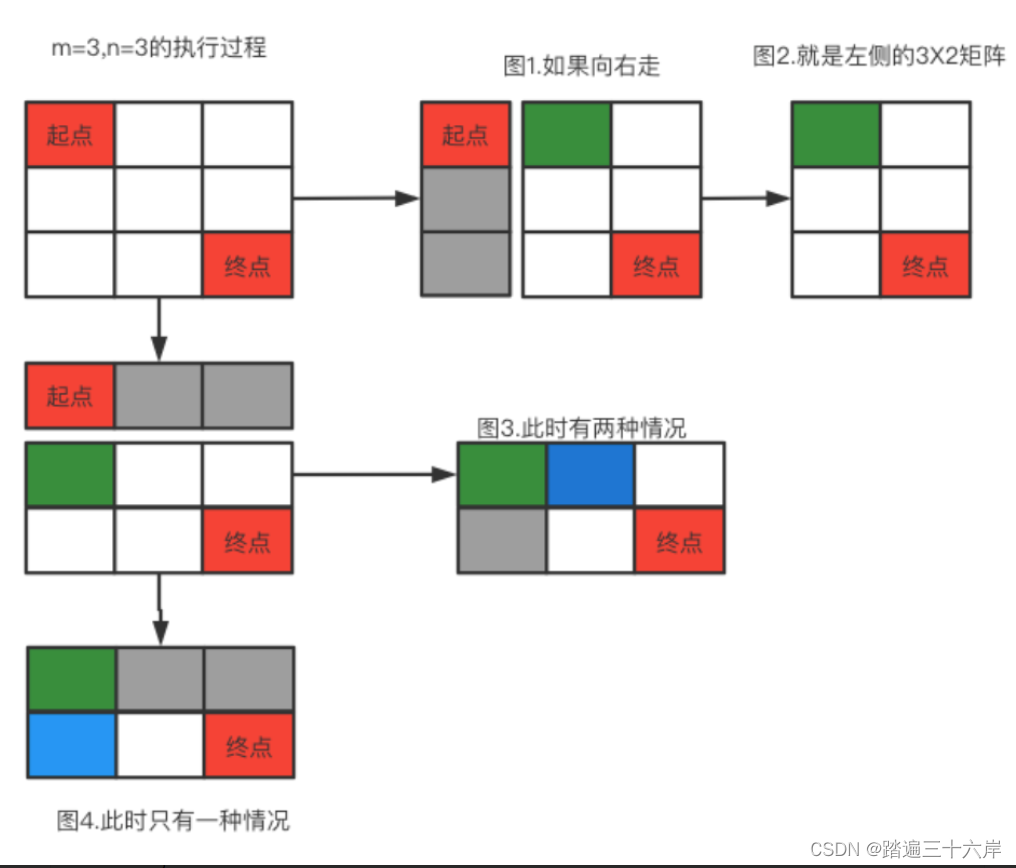
可以看到，一个3X3的矩阵下一步就变成了一个3X2或者2X3的矩阵，而总路径数，也是是两者各自的路径之和。
因此，对于一个mxn的矩阵，求路径的方法search(m,n)就是:search(m-1,n)+search(m,n-1);
递归的含义就是处理方法不变，但是问题的规模减少了

解析 :

注意 :递归的方式会超出时间限制

class Solution {public int uniquePaths(int m, int n) {return dp(m,n);}public int dp(int m,int n){if(n == 1 || m == 1){return 1;}return dp(m - 1,n) + dp(m,n - 1);}
} 

用二维数组优化递归

我们来优化递归的问题，研究如何结合二维数组来实现记忆化搜索.

从上面这个树也可以看到在递归的过程中存在重复计算的情况，例如1,1出现了两次，如果是一个NXN的空间，那 1.0 和 0,1 的后续计算也是一样的。从二维数组的角度，例如在位置(1,1)处，不管从(0,1)还是(1,0)到来，接下来都会产生2种走法，因此不必每次都重新遍历才得到结果。

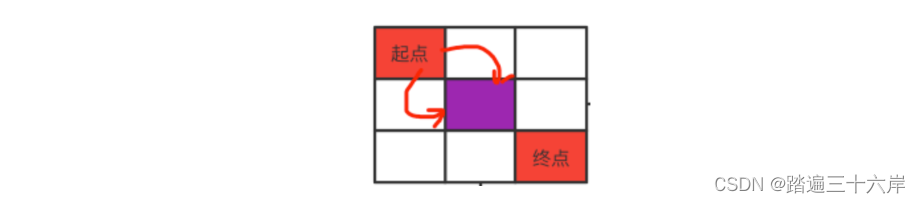
为此，我们可以采取一个二维数组来进行记忆化搜索，算好的就记录在数组中，也就是这样子:

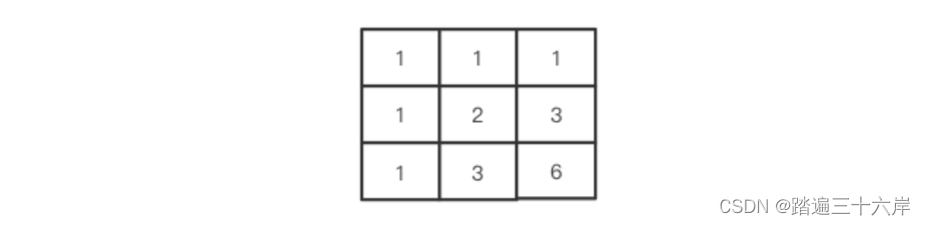
每个格子的数字表示从起点开始到达当前位置有几种方式，这样我们计算总路径的时候可以先查一下二维数组有没有记录，如果有记录就直接读，没有再计算，这样就可以大量避免重复计算，这就是记忆化搜索

根据上面的分析，我们可以得到两个规律:
1.第一行和第一列都是1。
2.其他格子的值是其左侧和上方格子之和。对于其他m，n的格子，该结论一样适用的，例如:

比如图中的4，是有上面的1和左侧的3计算而来，15是上侧的5和左侧的10计算而来。如果用公式表示就是:

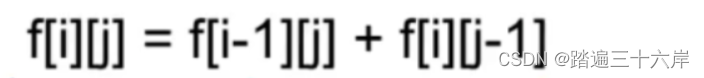
解析 :

class Solution {public int uniquePaths(int m, int n) {int[][] arr = new int[m][n];arr[0][0] = 1;for(int i = 0;i < m;i++){for(int j = 0;j < n;j++){if(i > 0 && j > 0){arr[i][j] = arr[i - 1][j] + arr[i][j - 1];}else if(i > 0){arr[i][j] = arr[i - 1][j];}else if(j > 0){arr[i][j] = arr[i][j - 1];}}}return arr[m - 1][n - 1];}
} 

拓展问题 : 最小路径和

描述 :

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

题目 :

LeetCode 64. 最小路径和 :

最小路径和 :

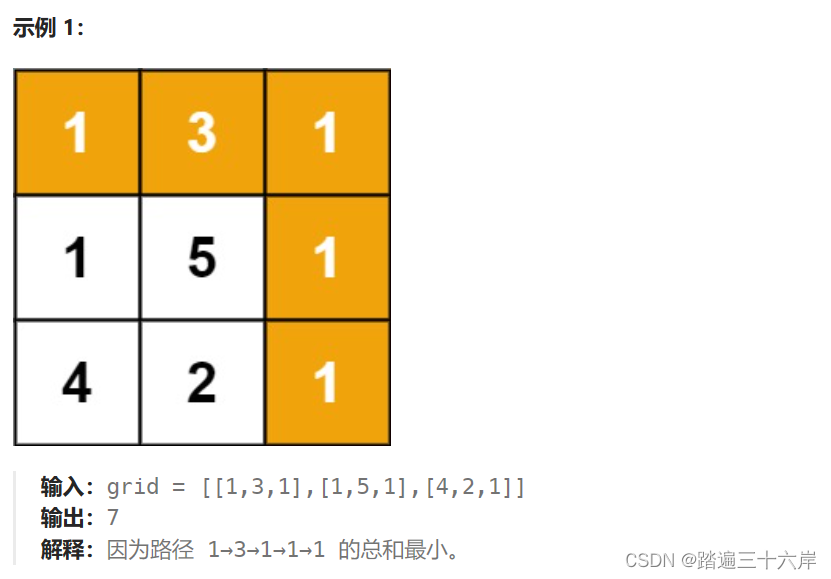
分析 :

这道题是在上面题目的基础上，增加了路径成本概念。由于题目限定了我们只能[往下]或者[往右]移动，因此我们按照当前位置可由哪些位置转移过来 进行分析:

• 当前位置只能通过[往下] 移动而来，即有f[i][j] = f[i-1][j] + grid[i][j]
• 当前位置只能通过[往右]移动而来，即有 f[i][j] = f[i][j-1] + grid[i][j]
• 当前位置既能通过[往下]也能[往右] 移动，即有f[i][j] = min(f[i][j - 1],f[i - 1][j]) + grid[i][j]

二维数组的更新过程，我们可以图示一下:

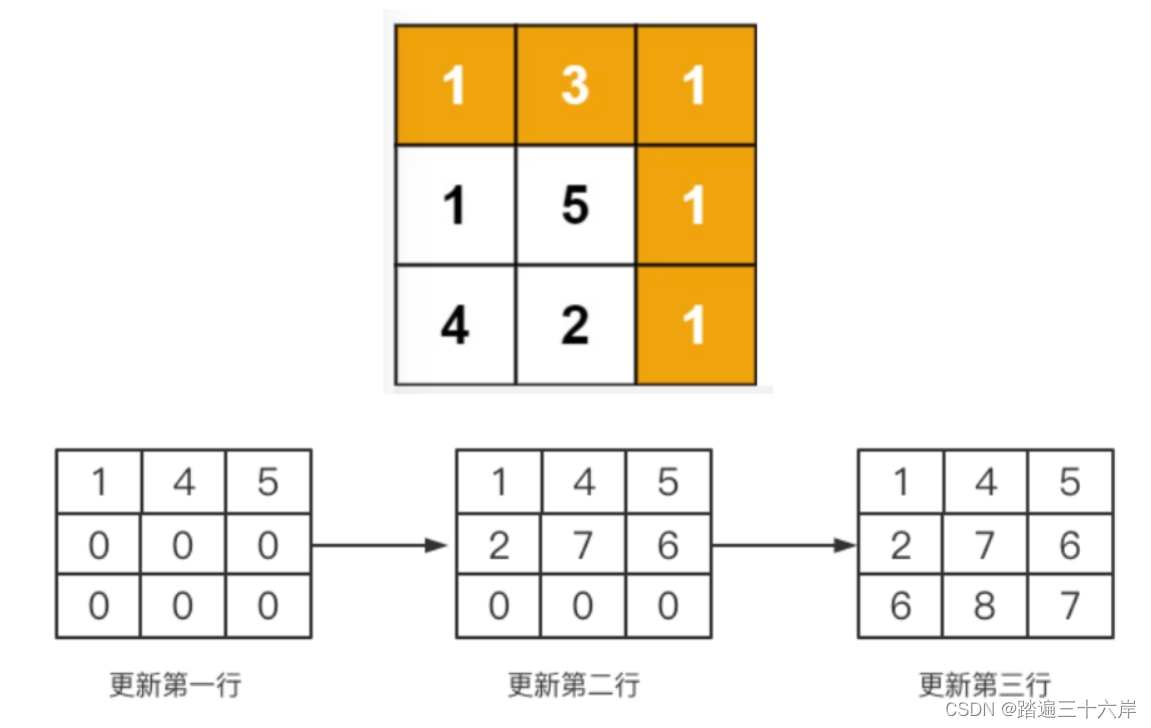
我们现在可以引入另外一个概念状态: 所谓状态就是下面表格更新到最后的二维数组,而通过前面格子计算后面格子的公式就叫状态转移方程。如果用数学表达就是:

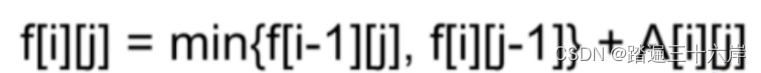
所谓的确定状态转移方程就是要找递推关系，通常我们会从分析首尾两端的变化规律来入手。

解析 :

class Solution {public int minPathSum(int[][] grid) {int m = grid.length;int n = grid[0].length;int[][] arr = new int[m][n];for(int i = 0;i < m;i++){for(int j = 0;j < n;j++){if(i == 0 && j == 0){arr[i][j] = grid[i];}else{int top = i - 1 >= 0 ? arr[i - 1][j] + grid[i][j] : Integer.MAX_VALUE; int left = j - 1 >= 0 ? arr[i][j - 1] + grid[i][j] :
Integer.MAX_VALUE;arr[i][j] = Math.min(top,left);}}}return arr[m - 1][n - 1];}
}

这期就到这里下期见 !

这篇关于算法通关第十九关-青铜挑战理解动态规划的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---