有趣的博弈（先手后手问题）

巴什博弈

两个聪明的人在玩一个游戏，当前有一堆n个石头，两个人每次可以从这堆石头当中取出[1,m]个石头，拿完石头的人赢得比赛。两个人每次得决策总是最利于自己的。 请问是先手赢还是后手赢。

再遇到此类问题时 需要将石头分为m+1堆,这时可以分为三种情况：

1.石头总数n小于等于m，那么先手一次就能拿完所有的石头，所以先手赢

2.石头总数n可以用k*(m+1)表示时，当先手拿走a个石头后手可以拿出m+1-a个石头此时石头堆的总数可以用(k-1)*(m+1)表示，先手拿走石头时后手总是可以维护(k-b)(m+1)个石头，直到最后一定是后手拿完石头，所以后手赢

3.石头总数n可以用k*(m+1)+x表示，此时先手拿走x个石头那么此时秩序又回到了第二种情况，所以先手一定赢

综上，当石头总数n能够整除m+1时后手赢，此外先手赢。

尼姆博弈

两个聪明的人在玩一个游戏，当前有n堆不同的石头，两个人在轮流拿取时可以将某一堆的石头拿走至少一个至多全部，不能不拿去且一轮只能在一堆石头里拿，最后一个将石头拿完的人获胜。请问是先手赢还是后手赢。

我们先考虑简单的情况

当n为1时，先手一定赢。当n为2时，用a，b表示两堆石头的数量，若a=b时先手拿去一定石头后导致a!=b但后手可以通过拿走另一堆相同的石头维持a=b的状态且两堆的石头总是在逐渐减少的直到a=b=0，所以此时后手总是赢，若a!=b时先手拿走某一堆的石头可以造成a=b的情况那么又回到了上一种情况但此时的先手是上一种情况的后手，所以a!=b的情况先手总是赢。那么我们现在可以将情况推广到n堆石头

我们引入尼姆和这一概念：将所有堆中的石头数量转化为二进制进行异或运算的结果则为尼姆和，当尼姆和为零时后手一定赢否则先手一定赢。这时我们发现此结论也是适用于以上n为1和2的情况的。

证明如下： 异或^：当两个数相等时为0不同时为1 (1^1=0,1^0=1,0^0=0,0^1=1)。同时我们给出两个定理：

 

1.当尼姆和为零时无论怎么拿去，拿去后的物品尼姆和一定不为零

2.当尼姆和不为零时，总是存在一种拿去的方法使得拿去后的物品尼姆和为零

思路：当尼姆和为零时先手方无论如何拿取，拿取后的尼姆和总是不为零，而后手方总是可以选择拿取的方式使得尼姆和再次为零同时石头的数量也在严格的减少当所以石头都拿完的情况也是尼姆和为零的情况所以后手一定赢。当尼姆和不为零时先手可以通过拿去使得尼姆和为零，那么此时先手一定赢。

那么现在只需要证明两个定理存在即可。

我们假设一堆石头由a1，a2，a3，a4，，，，an组成。假设当前密姆和为零也就是a1^a2^a3^a4^......^an=0 此时先手拿走一堆石头中的若干个石头后造成a1^a2^a3^a4^....^an=k 此时可以视为a1^a2^a3^a4^....^an^k=0

我们假设k转化为二进制后最高位1位于x位置那么在a1至an当中至少存在一个数ai使得ai的二进制第x位同样也为1（因为k的二进制第x位是由a1至an二进制第x位异或得来的，若该位置全为0则k的第x位也同样为0）我们可以拿去ai位置的石头使得ai位置的石头变为ai^k（这里ai^k一定是小于ai的，因为二进制第x位都为1那么异或后第x位为0，ai高于x的位 异或后不变，低于x的位因为x位异或后为0所以整个数一定减小）所以只需在ai位拿走ai-ai^k就可以使得尼姆和不为零的组合变为零。到这里我们已经证得第二个定理成立接下来只需要证明第一个定理

假设（a1，a2，a3，a4，，，an）尼姆和为a 拿取后（b1，b2，b3，b4，，，bn）尼姆和为b

b=0^b

 =(a^a)^b

 =a^(a^b)

 =a^(a1^a2^a3^a4，，，^an)^(b1^b2^b3^b4，，，^bn)

 =a^(ai)^(bi)

也就是拿走第i堆石头使得ai变为bi。若a为零因为ai!=bi所以b!=0。也就是当尼姆和为零时无论怎么拿去，拿去后的物品尼姆和一定不为零 那么第一个定理也就证明了

阶梯博弈（尼姆博弈进阶）

两个聪明的人在玩一个游戏，在n级阶梯的每一级上有不同的小石子，两个人可以依次进行一个操作：讲某一级阶梯阶梯上的石子至少一个至多全部放在低一级的阶梯上当某一人将阶梯上的石头全部拿走以至于下一人没有石头拿取时为获胜。

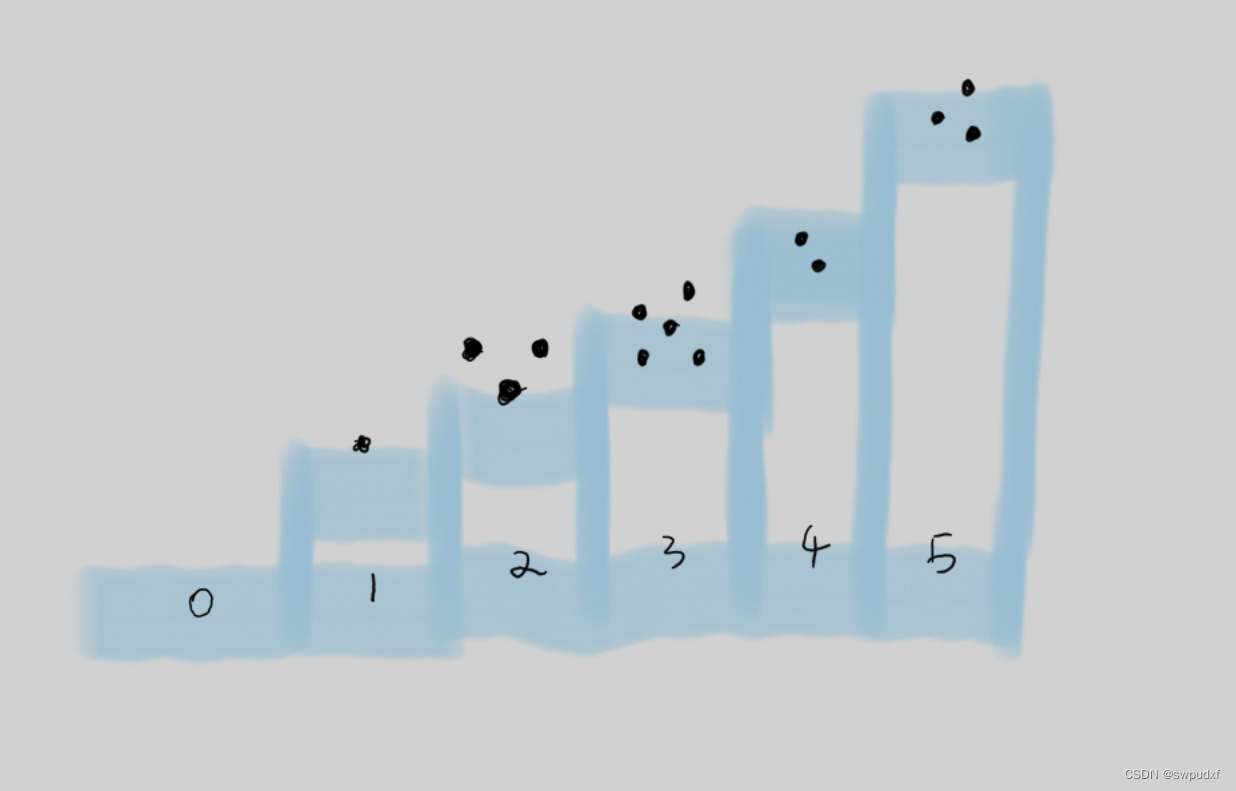
 如图所示为5级阶梯的例子 当所有石子被拿到地面上（0级阶梯）时游戏结束。

我们先只讨论奇数级阶梯的尼姆和，当尼姆和不为0时先手必胜否则后手必胜。证明如下：

 

先手进行一次拿取石头的操作将尼姆和改变为0，此时后手有两种操作方法 第一种是将奇数位的石子拿到偶数位试图通过减少某一奇数级的石子数量打破尼姆和为0的状态，但是之后先手仍可以通过移动某一奇数位的的石子到偶数位的操作维持尼姆和为0，第二种是将偶数位的石子拿到奇数位试图通过增加某一奇数级的石子数量打破尼姆和为零，但是之后先手仍可以把后手拿到该奇数级的石子相同数量的拿到更低一级的偶数位。我们可以发现这几种操作都是使阶梯石子一步一步往0阶梯移动的过程直到最后阶梯上没有石子也就是最终尼姆和为0的情况。但是尼姆和为0的情况总是在先手手上所已先手必胜