三部曲解下棋先手后手问题

1. 题目

两个人下棋，给定一个数组Arr={1,4,9,2,10,7};两个人只能从数组两端拿元素，得到获胜者的分数；

首先明确一下，这个游戏的最优解是先手必赢，但是如果是现实中两个人玩游戏就不一定了

2. 暴力递归解法

• 思路
  想得到优胜者的分数，优胜者一定是两个人中的一个，要不就是甲赢要不就是乙赢；甲赢的时候可能是先手也可能是后手，那么就可以看成甲先手(乙后手)得到的分数和甲后手(乙先手)得到的分数中的最大值；
  说明：函数f(Arr,L,R)表示在数组[L,R]范围开始到比赛结束，甲先手还能得到的分数最大值；函数s(Arr,L,R)表示在数组[L,R]范围开始到比赛结束，甲后手还能得到的分数最大值；

• code

int  f(vector<int>& Arr, int L, int R)//甲先手还能得到的分数
{if (L == R)return Arr[L];elsereturn max(Arr[L] + s(Arr, L + 1, R,dp), Arr[R] + s(Arr, L, R - 1));
}int s(vector<int>& Arr, int L, int R)//甲后手还能得到的分数
{if (L == R)return 0;elsereturn max(f(Arr, L + 1, R, dp), f(Arr, L, R - 1, dp));
}

• 3. 记忆搜索解法

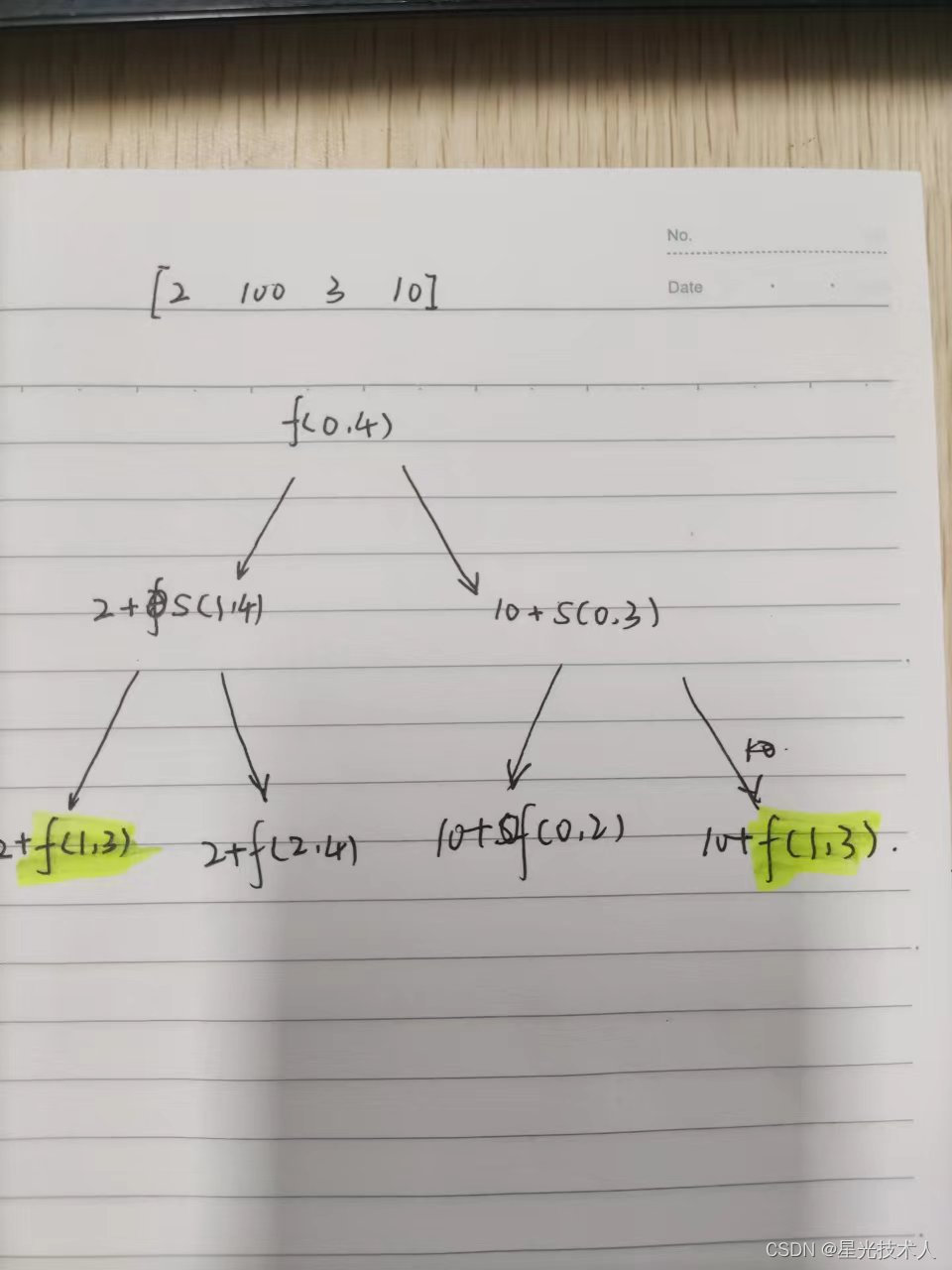
解法一存在重复计算的情况，假如状态数组，记录到达过的状态

• code

#include<iostream>
#include<vector>
using namespace std;class QQ
{
public:int  f(vector<int>& Arr, int L, int R, vector<vector<int>>& dp){if (dp[L][R] != -1)return dp[L][R];if (L == R)dp[L][R] = Arr[L];elsedp[L][R] = max(Arr[L] + s(Arr, L + 1, R,dp), Arr[R] + s(Arr, L, R - 1,dp));return dp[L][R];}int s(vector<int>& Arr, int L, int R, vector<vector<int>>& dp){if (dp[L][R] != -1)return dp[L][R];if (L == R)dp[L][R] = 0;elsedp[L][R] = max(f(Arr, L + 1, R, dp), f(Arr, L, R - 1, dp));return dp[L][R];}
};int main()
{QQ qq;vector<int> Arr = { 3,100,2,50 };int L = 0;int R = Arr.size();vector<vector<int>> dp(R, vector<int>(R,-1));int res = qq.s(Arr, L, R - 1,dp);cout << res << endl;return 0;
}

4. 严格表结构解法

定义两个表f和s，首先确定表中可以直接得出值得位置，然后确定位置依赖关系，确定遍历顺序；

• code

void code2(vector<int>& Arr, vector<vector<int>>& f, vector<vector<int>>& s)
{for (int i = 0; i < Arr.size(); i++)f[i][i] = Arr[i];int row = 0;int col = 1;while (col < Arr.size()){int m = row;int n = col;while (n < Arr.size()){f[m][n] = max(Arr[m] + s[m + 1][n], Arr[n] + s[m][n - 1]);s[m][n] = max(f[m][n - 1], f[m + 1][n]);m++;n++;}col++;}
}
int main()
{vector<int> Arr = { 3,100,70,50 };int R = Arr.size();vector<vector<int>> f(R, vector<int>(R, 0));vector<vector<int>> s(R, vector<int>(R, 0));code2(Arr, f, s);int res = max(f[0][R-1], s[0][R-1]);cout << res << endl;return 0;
}