本文主要是介绍YF的“愉快”一周(第二周),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
一,递归
A---判断整数N是否为素数
B---求组合数(高效递归版)
C---互质数判断(递归)
二,结构体
C++------------sort()排序
A---Zone Selection
B---BAN-PICK
三,C++ STL
什么是STL?
STL内容
容器分为两类
stack容器 C++ stack容器_CV敲击器的博客-CSDN博客
vector容器 CSDN
四,约瑟夫环问题
方法一(数组):
方法二(链表):
题目训练
A---狼人杀
B---Joseph
一,递归
递归的必须满足三个条件:
(1)必须有终止条件;
(2)递归的规模在递减(这里的值可以是增加的,但是规模要逐渐减小);
(3)循环能转换成递归,但递归不一定能变成循环;
大多数递归是数学问题,如果理解不来就把别人的程序看懂。
A---判断整数N是否为素数
对于整数N(N在int范围内),如果正整数N只能被1和N整除,则N为素数。
函数接口定义:
//判断一个整数n是否为素数int isPrime(int n);
裁判测试程序用例:
#include<stdio.h>
//判断一个数是否为素数
int isPrime(int);
int main()
{int m,i,k;while(scanf("%d",&m)==1){if(isPrime(m)){printf("prime\n");}else{printf("not prime\n");}}return 0;
}
// 你的代码将被嵌在这里输入样例1:
11
输出样例1:
prime
输入样例2:
4
输出样例2:
not prime难点:这题逻辑不难,要注意一些细节问题。
没有考虑到n不能小于等于0的情况,要用sqrt()否则会超时
AC代码
#include<math.h>
int isPrime(int n)
{if(n==1) return 0;if(n<=0) return 0;for(int i=2;i<=sqrt(n);i++){if(n%i==0) return 0;}return 1;
}B---求组合数(高效递归版)
请编写递归函数,求组合数。
![]()
![]()
函数原型
double Cmb(int x, int y);说明:x 和 y 为非负整数,且 x≥y。
裁判程序
#include <stdio.h>double Cmb(int x, int y);int main()
{int m, n;scanf("%d%d", &m, &n);printf("%.10g\n", Cmb(m, n));return 0;
}/* 你提交的代码将被嵌在这里 */要求:不要使用循环语句,不调用阶乘函数和排列数函数。找出递推公式,该函数直接调用自己求得结果。
输入样例
4 2输出样例
6输入样例2
34 17输出样例2
2333606220难点:不知道如何用递归写出代码。可以使用杨辉三角的思想:
C(x,y)=C(x-1,y)+C(x-1,y-1),但是运行太慢。
杨辉三角:
double Cmb(int x, int y)
{//杨辉三角的思想C(x,y)=C(x-1,y)+C(x-1,y-1)if(y==0||x==y) return 1;else return Cmb(x-1,y)+Cmb(x-1,y-1);
}AC代码(优化)
double Cmb(int x, int y)
{//杨辉三角的思想C(x,y)=C(x-1,y)+C(x-1,y-1)if(y==0||x==y) return 1;else if(y>x/2){ //当y过大时,将C(x,y)转换成C(x,x-y),减小计算量 y=x-y;Cmb(x,y);}else return x*Cmb(x-1,y-1)/y; //减少一次函数调用,效率更高
}C---互质数判断(递归)
要求实现一个递归函数,能够高效判断两个正整数a,b(0<a,b<109)是否为互质数(最大公约数为1)。
函数接口定义:
bool check(int a, int b);其中 a 、b是用户传入的参数,存放待判断是否为互质数的两个正整数。
裁判测试程序样例:
#include<iostream>
using namespace std;//输入n对整数,统计其中互质数的个数,处理到文件尾
int main() {int n;while(cin>>n) {int cnt=0;for(int i=0; i<n; i++) {int a,b;cin>>a>>b;if(check(a,b)==true) cnt++;}cout<<cnt<<endl;}return 0;
}输入样例:
3
3 11
5 11
10 12
输出样例:
2难点:不知道如何用递归写出代码。可以使用辗转相除法来判断
AC代码
int gcd(int a, int b) {if (b == 0) {return a;}return gcd(b, a % b);
}bool check(int a, int b) {return gcd(a, b) == 1;
}
二,结构体
C++------------sort()排序
从小到大
#include<iostream>
#include<algorithm>//sort()函数引用的文件
using namespace std;int main()
{int a[5]={5,4,3,2,1};sort(a,a+5);for(int i=0;i<5;i++) printf("%d ",a[i]); return 0;
}从大到小
#include<iostream>
#include<algorithm>//sort()函数引用的文件
using namespace std;bool cmp(int a,int b){return a>b;
} int main()
{int a[5]={1,2,3,4,5};sort(a,a+5,cmp);//插入一个cmp()函数,用来实现从大到小排序 for(int i=0;i<5;i++) printf("%d ",a[i]); return 0;
}结构体排序(从大到小)
#include<iostream>
#include<algorithm>//sort()函数引用的文件
using namespace std;struct Student
{string name;int score;
}s[10];bool cmp(Student a,Student b)//这里只用写结构体的一部分
{return a.score>b.score;
}int main()
{int n;cin>>n;for(int i=0;i<n;i++) cin>>s[i].name>>s[i].score;sort(s,s+n,cmp);//插入一个cmp()函数,用来实现从大到小排序 for(int i=0;i<n;i++) cout<<s[i].name<<" "<<s[i].score<<endl;return 0;
}A---Zone Selection
在第五人格巅峰七阶及以上的排位赛中,需要进行区域选择。我们将在本题中形式化、推广化的解决区域选择问题。
在地图中,共有 n 台密码机,第 i台密码机的坐标为 (xi,yi)。在推广化的游戏中,有 kk名求生者。每名求生者可以选择一台密码机作为其出生点,我们称被选择的密码机为 出生密码机。
监管者共有 T个出生点可供选择。第 i 个可能的出生点坐标为 (xi,yi)。此时,由于“封禁”天赋的存在,离监管者最远的密码机将不能被破译。
如果多台密码机与监管者的距离相同且最远,“封禁”天赋将会封禁这几台密码机中标号最小的那一台。
请问在该 TT 个出生点中,有多少出生点,可以使某一台 出生密码机 被封禁。
Input
输入共 n+T+k+1行。
输入的第一行为三个整数 n,k,T。
接下来 n行,每行两个整数 xi,yi表示一台密码机的坐标。
接下来 k行,每行两个整数 xi,yi表示一名求生者选择出生密码机的坐标,保证该坐标在上面出现过。
接下来 T 行,每行两个整数 xi,yi表示监管者的一个出生点。
Output
输出一行一个整数,为答案。
Sample 1
| Inputcopy | Outputcopy |
|---|---|
4 2 2 -1 0 0 -1 2 0 0 2 -1 0 0 2 3 0 0 0 | 1 |
Hint
【样例 #1 解释】
显然,第一台密码机和第四台密码机为出生密码机。
第一位监管者与位置在 (−1,0)(−1,0) 的第一台密码机距离最远,为 44。因此,第一台密码机被封禁。
第二位监管者与位置在 (2,0),(0,2)(2,0),(0,2) 的第三、四台密码机距离相同且最远,为 22。根据上面提到的规则,第三台密码机被封禁。
被封禁的出生密码机为 11 台。
【数据规模与约定】
对前 10%的数据,保证 n=k=1
对前 20%的数据,保证 n,k,t≤10
对另外 20%的数据,保证密码机与出生点的坐标中的 x 均为 0。
对另外 10%的数据,保证 n=k。
对另外 10%的数据,保证 T=1。
对于 100%的数据范围 1≤k≤n≤10^3, 1≤T≤10^3, 1≤∣xi∣,∣yi∣≤10^3
难点:题目太长,不容易理解。但如果一边看题一边画图,这题其实非常好做。
AC代码
#include<stdio.h>
#include<math.h>struct code//密码机
{int id;int x;int y;int flag;double d;
}c[1000];struct dmax//最大距离
{int t;int id;double d;
}max;double distence(int x1,int y1,int x2,int y2){return sqrt(1.0*((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)));
}int main()
{int n,k,T;scanf("%d%d%d",&n,&k,&T);int count=1;for(int i=0;i<n;i++){scanf("%d%d",&c[i].x,&c[i].y);c[i].flag=0;c[i].id=count;count++;}for(int i=0;i<k;i++){int x,y;scanf("%d%d",&x,&y);for(int j=0;j<n;j++){//如果出生点是求生者的出生点,则做一个标记 if(x==c[j].x&&y==c[j].y) c[j].flag=1;}}count=0;for(int i=0;i<T;i++){int x,y;max.d=0;scanf("%d%d",&x,&y);for(int j=0;j<n;j++){c[j].d=distence(x,y,c[j].x,c[j].y);if(c[j].d>max.d){//如果距离相同,则标记编号小的出生点。 max.d=c[j].d;max.t=j;max.id=c[j].id;}}if(c[max.t].flag==1) count++;//如果监管者“封禁”的刚好是求生者的出生点,则记录个数 }printf("%d",count);return 0;
}B---BAN-PICK
在第五人格职业联赛的每一场对局中,需要进行 Ban-Pick 流程。Ban 即角色禁用,Pick 即角色选用。
如试题 Winner 所述,游戏分为 求生者(SurvivorSurvivor) 与 监管者(HunterHunter) 两个阵营。求生者阵营 共有 nn 名角色,监管者阵营 共有 mm 名角色。
在某局比赛中,监管者 可以 ban(禁用) 掉 求生者阵营 55 名角色,求生者 可以 ban(禁用) 掉 监管者阵营 22 名角色。
每个角色,无论其属于求生者阵营还是监管者阵营,均可以使用 熟练度 来量化该阵营选手选择该角色的优先程度。选手一定会优先选择 熟练度 更高的角色进行游戏。
基于这样的考量,监管者选手 在进行 Ban 流程时,往往会选择 ban(禁用) 掉 求生者阵营熟练度最高 的若干名 求生者角色。同样,求生者选手 在进行 Ban 流程时,往往会选择 ban(禁用) 掉 监管者阵营熟练度最高 的若干名 监管者角色。
在 Ban 流程完成后,需要执行 Pick 流程。
如试题 Winner 所述,求生者选手 需要从 求生者阵营 中选择 44 名不同的角色,监管者选手 需要从 监管者阵营 中选择 11 名角色。
现在告诉你所有角色的名字、阵营与选手对其熟练度,请你给出双方阵营 Pick 的角色名字。
Input
输入共 n+m+1 行。
输入的第一行为两个整数 n,m分别代表求生者阵营角色数和监管者阵营角色数。
接下来 n+m 行,首先为一个仅由英文字母组成的字符串,代表该角色的姓名;接下来为一个大写字符
H或S,若为H,则代表该角色为监管者阵营,若为S,则代表该角色为求生者阵营;接下来一个正整数,代表该阵营选手对该角色的熟练度。上述字符串、大写字符、正整数之间由一个空格分隔。
Output
输出共 55 行。
输出的第一行为监管者阵营选择角色的角色名。
输出的第二到五行为求生者阵营选择角色的角色名,按照熟练度从高到低排列。
Sample 1
| Inputcopy | Outputcopy |
|---|---|
9 3 Amily S 1 Lydia S 2 Lisa S 4 Beck H 1 Freddie S 5 Cliche S 6 Aesop S 7 Eli S 8 Norton S 9 Tiletower H 3 Yidhra H 2 Emma S 3 | Beck Lisa Emma Lydia Amily |
Hint
输入输出样例 1 解释
求生者阵营角色:Amily,Lydia,Lisa,Freddie,Cliche,Aesop,Eli,Norton,Emma
监管者阵营角色:Beck,Tiletower,Yidhra
监管者选手将 ban 掉求生者阵营中角色 Norton,Eli,Aesop,Cliche,Freddie
求生者选手将 ban 掉监管者阵营中角色 Tiletower,Yidhra
数据规模与约定
对于前 20% 的数据,n=9,m=3
对于前 50%的数据,保证 n≤10^3, m≤10^3
对于前 70%的数据,保证 wi≤10^9
对于所有数据,保证 9≤n≤10^5, 3≤m≤10^5所有名字长度 ≤10.熟练度大小 wi满足 1≤wi≤10^18。保证每个阵营中熟练度互不相同。保证名字仅有大写字母和小写字母构成。
难点:代码容易超时,这里推荐使用C++的sort()函数
AC代码
#include<iostream>
#include <algorithm>
using namespace std;struct part
{string name;long long val;
}s[100005],h[100005]; //创建两个阵营 int cmp(part a,part b){//结构体排序格式 return a.val>b.val;
}int main()
{int n,m;scanf("%d%d",&n,&m);int sc=0,hc=0;for(int i=1;i<=n+m;i++){string name;char flag;long long x;cin>>name>>flag>>x;if(flag=='H') {//监管者阵营 ++hc;h[hc].name=name;h[hc].val=x;}if(flag=='S'){//求生者阵营 ++sc;s[sc].name=name;s[sc].val=x;}}sort(s + 1, s + sc + 1, cmp);sort(h + 1, h + hc + 1, cmp);//输出 cout << h[3].name << endl; for(int i=6;i<=9;i++){cout << s[i].name << endl;}return 0;
}三,C++ STL
什么是STL?

STL内容
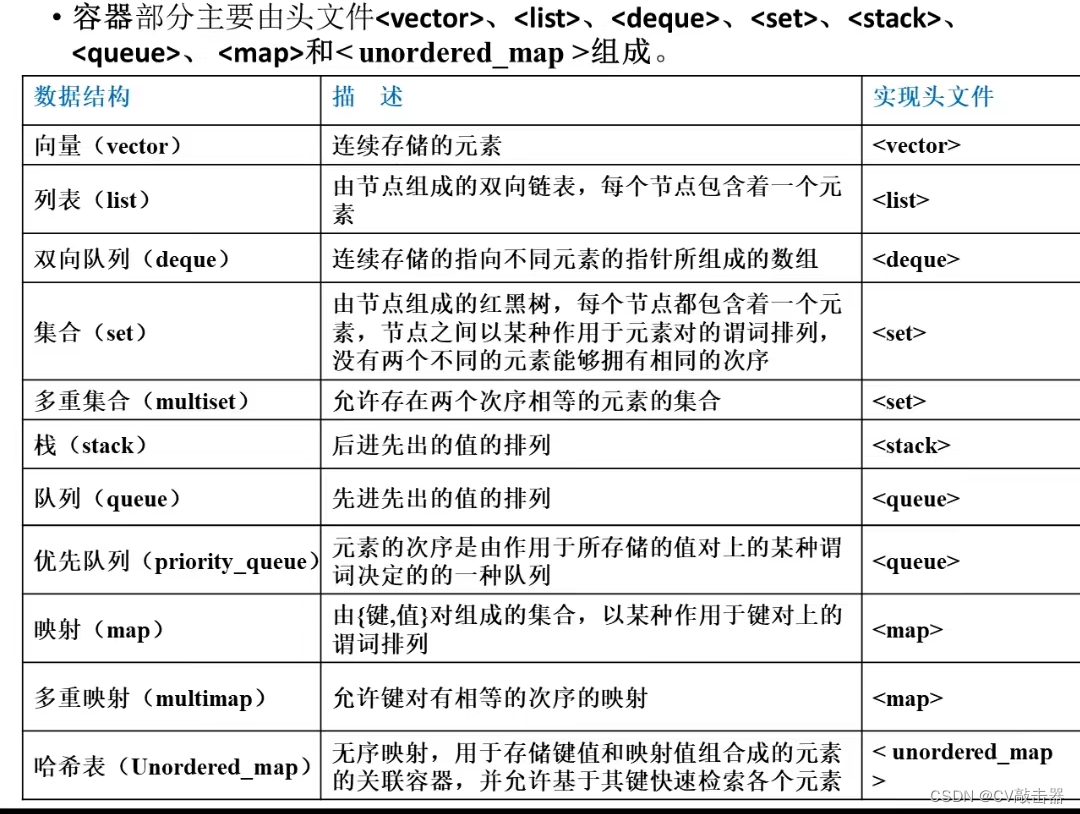
容器分为两类

stack容器 C++ stack容器_CV敲击器的博客-CSDN博客
vector容器 CSDN
四,约瑟夫环问题
约瑟夫环问题是一个很经典的问题:一个圈共有N个人(N为不确定的数字),第一个人的编号为0或者1(两个都可以,看你的程序如何编写),假设这边我将第一个人的编号设置为1号,那么第二个人的编号就为2号,第三个人的编号就为3号,第N个人的编号就为N号,现在提供一个数字M,第一个人开始从1报数,第二个人报的数就是2,依次类推,报到M这个数字的人出局,紧接着从出局的这个人的下一个人重新开始从1报数,和上面过程类似,报到M的人出局,直到N个人全部出局,请问,这个出局的顺序是什么?
方法一(数组):
#include<bits/stdc++.h>
using namespace std;
//用数组实现约瑟夫环问题
int a[110]={0}; //元素值为0表示未出局
//i既代表数组的下标,也代表每个人的编号
//k是用来计数的,一旦k的值达到m,代表此人需要出局,并且k需要重新计数,这样才能够找出所有需要出局的人
//数组的0代表未出局的人,数组非0代表出局的人,未出局的人需要报数,出局的人不需要报数
int main()
{int N,M;int cnt=0,i=0,k=0; //cnt表示目前出局的人数 cin>>N>>M; //表示总共有n人,数到数字m时出局 while(cnt!=N) //因为要求N个人的出局顺序,因此当cnt(用来统计已经出局的人)未达到n时,需要循环不断报数 {i++; //i是每个人的编号 if(i>N) i=1; //这里需要特别注意:i的值是不断累加的,一旦发现i的值>N,那么i需要重新从第1个人开始//数组要从第一个元素重新开始一个一个往后判断 if(a[i]==0) //只有元素值为0的人 才需要报数,元素值为非0的代表已经出局了,不用报数 {k++;if(k==M) //代表已经某个人已经报了M这个数,需要出局 {a[i]=1; //编号为i的这个人出局 cnt++; //出局的人数+1 cout<<i<<" "; //输出出局的人的编号 k=0; //清空k,让下一个人重新从1开始报数 }}}return 0;
} 方法二(链表):
#include<iostream>
using namespace std;
//用链表实现约瑟夫环问题 (循环链表) typedef struct node //typedef用来重命名struct node这种数据类型,将其命名为Node
{int data;struct node* next;
}Node;void ysflb(int N, int M) //总共有N个人,报到数字为M的人出局
{//初始化循环链表Node* head = NULL, * p = NULL, * r = NULL; //head为头指针,指向链表的第一个结点,一开始赋值为NULL,代表不指向任何结点 head = (Node*)malloc(sizeof(Node)); //让head指向一个实际的空间if (NULL == head) //内存空间可能会申请失败,大多数情况不会申请失败 {cout << "Memory Failed!";return;}head->data = 1; //从1开始编号 head->next = NULL; //一开始整个链表只有一个Node(结点),这个Node有两个域,分别是data和next//data从1开始,next指向NULL,总共需要N个结点,现在创建了一个,还需要N-1个 p = head; //head要保持不能改变,才能够找到链表的起始位置,一开始p也指向第一个结点//p等一下会被使用,用它可以便于创建剩下的N-1个结点 //尾插法创建链表,已经有一个1号结点了,还需要创建剩下的n-1个结点 for (int i = 2; i <= N; i++){r = (Node*)malloc(sizeof(Node));r->data = i;r->next = NULL;//插入结点 p->next = r;p = r;}//创建循环链表p->next = head; //最后一个结点的next指向头结点p = head; //为后续方便,将p指向头结点//约瑟夫环的模拟while (p->next != p) //如果p的next=p,说明目前只有一个元素 {for (int i = 1; i < M; i++) //报到数字为M的时候出局 {r = p; //保留出局的前一个结点 p = p->next; //p指向的是要出局的这个结点,需要保留前一个结点}// 输出cout << p->data << " ";r->next = p->next; //删除p的目的,此时p指向哪里? : p = p->next; //更新p重新进行报数 }cout << p->data;
}int main()
{int n, m;cin >> n >> m;ysflb(n,m);return 0;
}题目训练
A---狼人杀
“狼人杀”的原型是上世纪八十年代末,莫斯科大学心理学系的迪米特里·达维多夫发明了一种警察与杀手互猜身份的游戏,也就是“杀人游戏”。“杀人游戏”从一开始就只有核心规则得到了确定,本身是一款开源游戏。1990年以后,“杀人游戏”逐渐传播到了欧洲,随后到了美国,在每个不同的国家和地区都根据各自文化背景“演化”出了新的内容。
大哲是一个忠实的狼人杀爱好者,而且是高手中的高手。由于她过于擅长各类套路,并且具备敏锐的直觉与极强的心理素质,甚至还是一个心理学博士,她的朋友逐渐失去了游戏体验。为了照顾她的朋友,她决定制定一种不靠计谋、不用推理,全靠强运的“杀法”:
游戏玩家围成一个圈,从指定的第一个人开始数数,数到第 m 个人时,那个人就会被处死。之后从被处死的人的后一个人开始数数,再数到第 m 个人处死......依此方法不断杀死玩家。假如说玩家有好人与坏人两种身份,每种身份各 n 人,试问如何安排这些人的座位,能使得在处死 n 人后,剩下的 n 人都是好人
Input
多组数据,每组数据输入:好人和坏人的人数n(<=32767)、步长m(<=32767);
Output
对于每一组数据,输出2n个大写字母,‘G’表示好人,‘B’表示坏人,50个字母为一行,不允许出现空白字符。相邻两组输出之间有一个空行隔开。
Sample
| Inputcopy | Outputcopy |
|---|---|
2 3 2 4 | GBBG BGGB |
AC代码
#include<stdio.h>struct player
{int id;int flag;char role;
}p[33000];//创建玩家void check(int n, int m, struct player p[33000]);//好人和坏人的判断int main()
{int n, m;while (~scanf("%d%d", &n, &m)) {check(2 * n, m, p);for (int i = 1; i <= 2 * n; i++) printf("%c", p[i].role);printf("\n\n");}return 0;
}void check(int n, int m, struct player p[33000])
{for (int i = 1; i <= n; i++) {p[i].flag = 0;p[i].id = i;p[i].role = 'G';//首先全部初始化为好人}int die = 0, k = 0, i = 0;while (die != n / 2) {i++;if (i > n) i = 1;if (p[i].flag == 0) {k++;if (k == m) {p[i].role = 'B';//出局的赋值为坏人p[i].flag = 1;//printf("%d ",i);die++;k = 0;}}}return;
}B---Joseph
The Joseph's problem is notoriously known. For those who are not familiar with the original problem: from among n people, numbered 1, 2, . . ., n, standing in circle every mth is going to be executed and only the life of the last remaining person will be saved. Joseph was smart enough to choose the position of the last remaining person, thus saving his life to give us the message about the incident. For example when n = 6 and m = 5 then the people will be executed in the order 5, 4, 6, 2, 3 and 1 will be saved.
Suppose that there are k good guys and k bad guys. In the circle the first k are good guys and the last k bad guys. You have to determine such minimal m that all the bad guys will be executed before the first good guy.
Input
The input file consists of separate lines containing k. The last line in the input file contains 0. You can suppose that 0 < k < 14.
Output
The output file will consist of separate lines containing m corresponding to k in the input file.
Sample
| Inputcopy | Outputcopy |
|---|---|
3 4 0 | 5 30 |
AC代码
#include <iostream>
using namespace std;
int main()
{int k, m,j;int s; //s为每次删除的位置int n; //n为总人数,即2kint a[14] = { 0 }; //数组a用来存储k(1到13)对应的mwhile (1){cin >> k;if (k == 0){break;}m = k; //m从k开始递增n = 2 * k;if (a[k] == 0) //即这个k还没有对应的m{while (1){s = 0;for (j = 0; j < k; j++){s = (s + m - 1) % (n-j); //这是每次删除的位置if (s < k) //杀了好人,不合规矩{break;}}if (j == k) break;m++;}a[k] = m;}cout << a[k] << endl;}return 0;
}这篇关于YF的“愉快”一周(第二周)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!